
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Диполь и расчёт поля диполя.Содержание книги
Поиск на нашем сайте
Понятие о потенциале электростатического поля. Существуют две характеристики электрического поля. В любой точке пространства поле можно задать либо вектором напряжённости — это «силовая» характеристика поля, либо потенциалом — это его энергетическая характеристика. Потенциал — энергетическая характеристика поля, связанная и с энергией заряда в электростатическом поле и с работой, совершаемой электрической силой при перемещении заряда. Электростатический потенциал равен отношению потенциальной энергии взаимодействия заряда с полем к величине этого заряда:
В СИ за единицу разности потенциалов принимают вольт (В) 11.Связь потенциала и напряженности, эквипотенциальне поверхности.
Из определения Градиента следует что т. е. напряженность Е поля равна градиенту потенциала со знаком минус. Знак минус говорит о том, что вектор напряженности Е поля направлен в сторону уменьшения потенциала. Эквипотенциальные поверхости: Для графического представления распределения потенциала электростатического поля, как и в случае поля тяготения, пользуются эквипотенциальными поверхностями — поверхностями, во всех точках которых потенциал φ имеет одинаковое значение. Если поле создается точечным зарядом, то его потенциал, согласно формуле потенциала поля точечного заряда, φ=(1/4πε0)Q/r. эквипотенциальные поверхности— концентрические сферы с цетром в точечном заряде. Линии напряженности всегда перпендикулярны к эквипотенциальным поверхностям. все точки эквипотенциальной поверхности обладают одинаковым потенциалом, поэтому работа по перемещению заряда вдоль этой поверхности равна нулю, т. е. электростатические силы, которые действуют на заряд, всегда направлены по перпендикурярам к эквипотенциальным поверхностям. вектор Е всегда перпендикулярен к эквипотенциальным поверхностям, поэтому линии вектора Е перпендикулярны этим поверхностям. Эквипотенциальных поверхностей вокруг каждого заряда и каждой системы зарядов можно провести бесконечное множество. их проводят так, чтобы разности потенциалов между любыми двумя соседними эквипотенциальными поверхностями были равны друг другу. Тогда густота эквипотенциальных поверхностей наглядно характеризует напряженность поля в разных точках. Там, где гуще расположены эти поверхности, напряженность поля больше.
Поляризация диэлектриков. Поляризация диэлектриков — явление, связанное с ограниченным смещением связанных зарядов в диэлектрике или поворотом электрических диполей, обычно под воздействием внешнего электрического поля, иногда под действием других внешних сил или спонтанно. Поляризацию диэлектриков характеризует вектор электрической поляризации. Физический смысл вектора электрической поляризации — это дипольный момент, отнесенный к единице объема диэлектрика. Иногда вектор поляризации коротко называют просто поляризацией. Поляризация — состояние диэлектрика, которое характеризуется наличием электрического дипольного момента у любого (или почти любого) элемента его объема. Различают поляризацию, наведенную в диэлектрике под действием внешнего электрического поля, и спонтанную (самопроизвольную) поляризацию, которая возникает в сегнетоэлектриках в отсутствие внешнего поля. В некоторых случаях поляризация диэлектрика (сегнетоэлектрика) происходит под действием механических напряжений, сил трения или вследствие изменения температуры. Поляризация не изменяет суммарного заряда в любом макроскопическом объеме внутри однородного диэлектрика. Результирующая напряженность поля Е внутри диэлектрика Е=Е0-Е1. В зависимости от механизма поляризации, поляризацию диэлектриков можно подразделить на следующие типы: Электронная, Ионная, Дипольная, Структурная, Резонансная. 13. Сегнето, пьезо, проводники, бла бла.. Сегнетоэле́ктрики - твёрдые диэлектрики обладающие в определённом интервале температур собственным электрическим дипольным моментом, который может быть переориентирован за счёт приложения внешнего электрического поля. Пьезоэле́ктрики — диэлектрики, в которых наблюдается пьезоэффект, то есть те, которые могут либо под действием деформации индуцировать электрический заряд на своей поверхности (прямой пьезоэффект), либо под влиянием внешнего электрического поля деформироваться (обратный пьезоэффект ) Если внутри проводника электрического поле отсутствует, то потенциал во всех точках внутри проводника одинаков (φ = const), т. е. поверхность проводника в электростатическом поле является эквипотенциальной. Это означает, что вектор напряженности поля на внешней поверхности проводника направлен по перпендикуляру к каждой точке его поверхности. Если это было бы не так, то под действием касательной составляющей Е заряды начали бы перемещаться по поверхности проводника, что, в свою очередь, противоречило бы равновесному распределению зарядов. Если во внешнее электростатическое поле поместить нейтральный проводник, то свободные заряды (электроны, ионы) будут совершать движение: положительные — по полю, отрицательные — против поля.Если во внешнее электростатическое поле поместить нейтральный проводник, то свободные заряды (электроны, ионы) будут совершать движение: положительные — по полю, отрицательные — против поля. Явление перераспределения поверхностных зарядов на проводнике во внешнем электростатическом поле называется электростатической индукцией. Закон Джоуля – Ленца Количество теплоты, которое выделяется в проводнике с током, пропорционально квадрату силы тока, времени его прохождения и сопротивлению проводника.
Закон Джоуля—Ленца можно представить в дифференциальной форме. Для этого выделим в проводнике элементарный цилиндрический объем
Количество теплоты, выделяющееся за единицу времени в единице объема, называют удельной тепловой мощностью тока:
24. Правило Кирхгофа. Первое правило Кирхгофа:
Это правило можно сформулировать и так: количество зарядов, приходящих в данную точку проводника за некоторое время, равно количеству зарядов, уходящих из данной точки за то же время. Второе правило Кирхгофа: В любом замкнутом контуре разветвленной цепи алгебраическая сумма ЭДС равна алгебраической сумме произведений токов на сопротивления соответствующих участков этого контура:
Диполь и расчёт поля диполя. Электрический Диполь – это система состоящая из двух одинаковых по величине, но противоположных зарядов, находящихся на малом расстоянии друг от друга по сравнению с расстоянием до других точек электрического поля. Вектор L проведённый от – к +, по модулю равный расстоянию между зарядами называется плечом Диполя.
1 Напряжённость поля Диполя в точке А на оси Диполя
2. Напряжённость поля в точке В на перпендикуляре восстановленном к середине Диполя
Видно, что поле на оси Диполя в 2 раза больше поля на перпендикуляре.
5. Поток вектора напряжённости. Теорема Остроградского-Гаусса для электростатических полей в вакууме.
В каждой точке поверхности S 1 проекция теорема Гаусса для одного заряда. – теорема Гаусса для нескольких зарядов
6. Поле бесконечной заряжённой плоскости, двух разноимённо заряжённых плоскостей, заряжённой сферы.
Рассмотрим поле, создаваемое бесконечной однородно заряженной плоскостью с везде одинаковой поверхностной плотностью заряда Линии напряжённости паралельны боковым её сторонам т.е не пронизывают их т.е поток через них равен 0. Таким образом линии пронизывают стороны основнаний и получим: Напряжённость бесконечной плоскости определяется:
Поле заряжённой сферы радиусом R При выборе в качестве замкнутой поверхности сферы радиусом R, напряжённость вычисляется аналогично:
7. Поле равномерно заряженного шара, Поле бесконечно заяженного цилиндра(нити ) Шар:
Поле бесконечно прямой равномерно заряженной нити с
8.Работа электростатического поля: Пусть электростатическое поле образованно зарядом Q>0. Пусть в этом поле по произвольной траектории перемещается другой точечный положительный заряд Q0 из точки 1 в 2.
Полная работа совершаемая полем на всем участке пути:
Значение работы зависит от положения начальной и конечной точек пути. Таким образом электростатические поля являются потенциальными, а кулоновские силы – консервативными. Работа совершаемая позамкнотому контуру пути будет равна 0, т.е.:
9.циркуляция вектора напряженности электростатического поля Если в качестве заряда Q0, которого перемещают в электростатическом поле, взять единичный точечный положительный заряд, то произведение Интеграл
|
|||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 1176; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.19.89 (0.006 с.) |

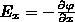
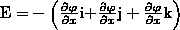 где i, j, k — единичные векторы координатных осей х, у, z.
где i, j, k — единичные векторы координатных осей х, у, z.
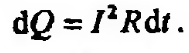
 , сопротивление которого
, сопротивление которого 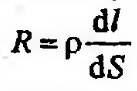 . Согласно закону Джоуля – Ленца:
. Согласно закону Джоуля – Ленца:
 или
или  -закон Джоуля—Ленца в дифференциальной форме.
-закон Джоуля—Ленца в дифференциальной форме. Алгебраическая сумма токов, сходящихся в узле, равна нулю:
Алгебраическая сумма токов, сходящихся в узле, равна нулю: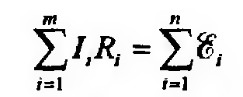



 Для данной конфигурации поток вектора напряженности через произвольную элементарную площадку d S будет равен:
Для данной конфигурации поток вектора напряженности через произвольную элементарную площадку d S будет равен: 
 на направление внешней нормали одинакова и равна:
на направление внешней нормали одинакова и равна:  тогда поток через S 1
тогда поток через S 1  Подсчитаем поток через сферу S 2, имеющую радиус R 2:
Подсчитаем поток через сферу S 2, имеющую радиус R 2:  Из непрерывности линии
Из непрерывности линии  следует, что поток и через любую произвольную поверхность S будет равен этой же величине:
следует, что поток и через любую произвольную поверхность S будет равен этой же величине: Полученный результат справедлив не только для одного заряда, но и для любого числа произвольно расположенных зарядов, находящихся внутри поверхности:
Полученный результат справедлив не только для одного заряда, но и для любого числа произвольно расположенных зарядов, находящихся внутри поверхности:

 . Представим себе мысленно цилиндр с образующими, перпендикулярными к заряженной плоскости, и основаниями (площадью
. Представим себе мысленно цилиндр с образующими, перпендикулярными к заряженной плоскости, и основаниями (площадью  каждое), расположенными относительно плоскости симметрично.
каждое), расположенными относительно плоскости симметрично.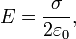

 , при
, при 
 при
при 

 :
: /
/ , при r>R
, при r>R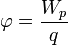




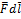 будет численно равно
будет численно равно  , тогда:
, тогда: (3)
(3) называется циркуляцией вектора напряженности. Значит, циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю. Силовое поле, которое обладает свойством (3), называется потенциальным. Из равенства нулю циркуляции вектора Е следует, что линии напряженности электростатического поля не могут быть замкнутыми, они обязательно начинаются на положительных зарядах, а заканчиваются на отрицательных.
называется циркуляцией вектора напряженности. Значит, циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю. Силовое поле, которое обладает свойством (3), называется потенциальным. Из равенства нулю циркуляции вектора Е следует, что линии напряженности электростатического поля не могут быть замкнутыми, они обязательно начинаются на положительных зарядах, а заканчиваются на отрицательных.


