
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Энергия заряженного проводника и конденсатора. Плотность энергии электростатического поля.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Энергия заряженного проводника и конденсатора. Если уединенный проводник имеет заряд q, то вокруг него существует электрическое поле, потенциал которого на поверхности проводника равен
При переносе заряда dq с проводника в бесконечность такую же работу совершают силы электростатического поля. Следовательно, при увеличении заряда проводника на величину dq возрастает потенциальная энергия поля, т.е.
Проинтегрировав данное выражение, найдем потенциальную энергию электростатического поля заряженного проводника при увеличении его заряда от нуля до q:
Применяя соотношение
Для заряженного конденсатора разность потенциалов (напряжение) равна 1. Энергия заряженного проводника и конденсатора. Если уединенный проводник имеет заряд q, то вокруг него существует электрическое поле, потенциал которого на поверхности проводника равен
При переносе заряда dq с проводника в бесконечность такую же работу совершают силы электростатического поля. Следовательно, при увеличении заряда проводника на величину dq возрастает потенциальная энергия поля, т.е.
Проинтегрировав данное выражение, найдем потенциальную энергию электростатического поля заряженного проводника при увеличении его заряда от нуля до q:
Применяя соотношение
Для заряженного конденсатора разность потенциалов (напряжение) равна
2. Плотность энергии электростатического поля. Это физическая величина, численно равная отношению потенциальной энергии поля, заключенной в элементе объема, к этому объему. Для однородного поля объемная плотность энергии равна
12. Носители тока в средах. Сила и плотность тока. Уравнение непрерывности. Электрическое поле в проводнике с током. Силовые линии электрического поля и линии тока. Электрический ток — упорядоченное некомпенсированное движение свободных электрически заряженных частиц, например, под воздействием электрического поля. Такими частицами могут являться: в проводниках — электроны, в электролитах — ионы (катионы и анионы), в газах — ионы и электроны, в вакууме при определенных условиях — электроны, в полупроводниках — электроны и дырки (электронно-дырочная проводимость). Сила тока — скалярная физическая величина, определяемая отношением заряда Δq, проходящего через поперечное сечение проводника за некоторый промежуток времени Δt, к этому промежутку времени.
Единицей силы тока в СИ является ампер (А). Если сила тока и его направление со временем не изменяются, то ток называется постоянным. Единица силы тока — основная единица в СИ 1 А — есть сила такого неизменяющегося тока, который, проходя по двум бесконечно длинным параллельным прямолинейным проводникам очень маленького сечения, расположенным на расстоянии 1 м друг от друга в вакууме, вызывает силу взаимодействия между ними 2·10-7 Η на каждый метр длины проводников. Рассмотрим, как зависит сила тока от скорости упорядоченного движения свободных зарядов. Выделим участок проводника площадью сечения S и длиной Δl (рис. 1). Заряд каждой частицы q0. В объеме проводника, ограниченном сечениями 1 и 2, содержится nSΔl частиц, где n — концентрация частиц. Их общий заряд
Если средняя скорость упорядоченного движения свободных зарядов
Таким образом, сила тока в проводнике зависит от заряда, переносимого одной частицей, их концентрации, средней скорости направленного движения частиц и площади поперечного сечения проводника. Заметим, что в металлах модуль вектора средней скорости упорядоченного движения электронов Плотность тока j — это векторная физическая величина, модуль которой определяется отношением силы тока I в проводнике к площади S поперечного сечения проводника, т.е.
В СИ единицей плотности тока является ампер на квадратный метр (А/м2). Как следует из формулы (1), Уравнение непрерывности. Представим себе, в некоторой проводящей среде, где течет ток, замкнутую поверхность S. Для замкнутых поверхностей векторы нормалей, а следовательно, и векторы
Из (7.3.1) и постоянства значения I во всех участках цепи постоянного тока следует, что плотности постоянного тока в различных поперечных сечениях 1 и 2 цепи обратно пропорциональны площадям
Пусть S – замкнутая поверхность, а векторы
Это соотношение называется уравнением непрерывности. Оно является, по существу, выражением закона сохранения электрического заряда. Дифференциальная форма записи уравнения непрерывности записывается так:
В случае постоянного тока, распределение зарядов в пространстве должно оставаться неизменным:
это уравнение непрерывности для постоянного тока (в интегральной форме). Линии
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 1818; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.11.13 (0.011 с.) |

 , а емкость - С. Увеличим заряд на величину dq. При переносе заряда dq из бесконечности должна быть совершена работа равная
, а емкость - С. Увеличим заряд на величину dq. При переносе заряда dq из бесконечности должна быть совершена работа равная  . Но потенциал электростатического поля данного проводника в бесконечности равен нулю
. Но потенциал электростатического поля данного проводника в бесконечности равен нулю  . Тогда
. Тогда


 , можно получить следующие выражения для потенциальной энергии W:
, можно получить следующие выражения для потенциальной энергии W:
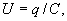 поэтому соотношение для полной энергии его электростатического поля имеют вид: 11. Энергия заряженного проводника и конденсатора. Плотность энергии электростатического поля.
поэтому соотношение для полной энергии его электростатического поля имеют вид: 11. Энергия заряженного проводника и конденсатора. Плотность энергии электростатического поля.

 . Для плоского конденсатора, объем которого Sd, где S - площадь пластин, d - расстояние между пластинами, имеем:
. Для плоского конденсатора, объем которого Sd, где S - площадь пластин, d - расстояние между пластинами, имеем: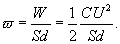 С учетом, что
С учетом, что  и
и  :
: или
или  .
.
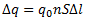

 , то за промежуток времени
, то за промежуток времени  все частицы, заключенные в рассматриваемом объеме, пройдут через сечение 2. Поэтому сила тока:
все частицы, заключенные в рассматриваемом объеме, пройдут через сечение 2. Поэтому сила тока:

 . Направление вектора плотности тока
. Направление вектора плотности тока  совпадает с направлением вектора скорости упорядоченного движения
совпадает с направлением вектора скорости упорядоченного движения  положительно заряженных частиц. Плотность постоянного тока постоянна по всему поперечному сечению проводника.
положительно заряженных частиц. Плотность постоянного тока постоянна по всему поперечному сечению проводника. принято брать наружу, поэтому интеграл
принято брать наружу, поэтому интеграл 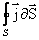 дает заряд, выходящий в единицу времени наружу из объема V, охваченного поверхностью S. Мы знаем, что плотность постоянного электрического тока одинакова по всему поперечному сечению S однородного проводника. Поэтому для постоянного тока в однородном проводнике с поперечным сечением S сила тока:
дает заряд, выходящий в единицу времени наружу из объема V, охваченного поверхностью S. Мы знаем, что плотность постоянного электрического тока одинакова по всему поперечному сечению S однородного проводника. Поэтому для постоянного тока в однородном проводнике с поперечным сечением S сила тока: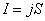
 и
и  этих сечений (рис. 7.2):
этих сечений (рис. 7.2): .
.

 . Тогда поток вектора
. Тогда поток вектора  сквозь эту поверхность S равен электрическому току I, идущему вовне из области, ограниченный замкнутой поверхностью S. Следовательно, согласно закону сохранения электрического заряда, суммарный электрический заряд q, охватываемый поверхностью S, изменяется за время
сквозь эту поверхность S равен электрическому току I, идущему вовне из области, ограниченный замкнутой поверхностью S. Следовательно, согласно закону сохранения электрического заряда, суммарный электрический заряд q, охватываемый поверхностью S, изменяется за время  на
на  , тогда в интегральной форме можно записать:
, тогда в интегральной форме можно записать: .
.
 или
или 
 следовательно,
следовательно,
 . Если ток постоянный, то избыточный заряд внутри однородного проводника всюду равен нулю. В самом деле, т.к. для постоянного тока справедливо уравнение
. Если ток постоянный, то избыточный заряд внутри однородного проводника всюду равен нулю. В самом деле, т.к. для постоянного тока справедливо уравнение  , то
, то Избыточный заряд может появиться только на поверхности проводника в местах соприкосновения с другими проводниками, а также там, где проводник имеет неоднородности.
Избыточный заряд может появиться только на поверхности проводника в местах соприкосновения с другими проводниками, а также там, где проводник имеет неоднородности.


