
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
I.9. Энергия электростатического поляСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Электростатические силы взаимодействия консервативны, следовательно, система зарядов обладает потенциальной энергией. Пусть имеется уединенный проводник, заряд емкость и потенциал которого соответственно равны
где Работа, совершаемая при увеличении потенциала проводника от 0 до
Энергия заряженного уединенного проводника равна той работе, которую необходимо совершить, чтобы зарядить этот проводник, то есть
Определим энергию заряженного конденсатора. Если
Следовательно, работа по увеличению заряда конденсатора от 0 до
Соответственно, энергия заряженного конденсатора
Учитывая, что конденсатор – это система из двух проводников 1 и 2,
Отсюда вытекает, что энергия системы из n неподвижных заряженных проводников
где Используя выражение (1.47), можно определить механическую силу,
откуда
где
Тогда искомая механическая (пондеромоторная) сила равна
где знак «минус» указывает, что сила F является силой притяжения. Преобразуем выражение (1.47), подставив в него
где Объемная плотность энергии (энергия единицы объема) электростатического поля определяется как
Краткие выводы · Электрическое поле – это особая форма существования материи, связанная с электрическими зарядами и осуществляющая взаимодействие между заряженными телами. Электрический заряд является физической величиной, определяющей интенсивность электромагнитных взаимодействий. · Суммарный заряд электрически изолированной системы не изменяется (закон сохранения электрического заряда). Электрические заряды не создаются и не исчезают, они лишь передаются от одного тела к другому или перераспределяются внутри данного тела. · Раздел электродинамики, в котором изучается взаимодействие неподвижных электрических зарядов, называется электростатикой. Такое взаимо-действие осуществляется посредством электростатического поля. · Неподвижные точечные электрические заряды взаимодействуют
· Силовой характеристикой электростатического поля является напряженность. Она численно равна силе, действующей со стороны поля на единичный положительный заряд, помещенный в данную точку поля:
· Напряженности полей, создаваемых отдельными зарядами, складываются геометрически (принцип суперпозиции):
· Электростатическое поле является потенциальным, то есть работа, совершаемая при перемещении заряда, не зависит от траектории, а определяется лишь начальным и конечным положениями заряда. Эта работа численно равна изменению потенциальной энергии:
· Энергетической характеристикой поля является потенциал. Он характеризует потенциальную энергию, которой обладал бы положительный
· Потенциал в какой-либо точке электрического поля, образованного системой зарядов, равен алгебраической сумме потенциалов, создаваемых каждым зарядом системы:
· Разность потенциалов – это скалярная физическая величина, опре-деляемая работой, совершаемой кулоновскими силами при перемещении положительного единичного заряда из одной точки поля в другую:
· Силовая и энергетическая характеристики поля связаны между собой соотношением
то есть напряженность поля равна градиенту потенциала со знаком «минус». Это означает, что вектор напряженности электростатического поля направлен в сторону убывания потенциала. В случае однородного поля (например,
· Вычисление напряженности поля большой системы электрических
то есть поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на электрическую постоянную. · При внесении диэлектрика во внешнее электрическое поле происходит его поляризация. Поляризованный диэлектрик создает собственное поле, которое внутри диэлектрика ослабляет внешнее электрическое поле в
Теорема Гаусса для электростатического поля в диэлектрике формулируется следующим образом: поток вектора смещения электростатического поля в диэлектрике сквозь произвольную замкнутую поверхность равен
· Способность проводника накапливать электрические заряды характеризуется электрической емкостью: Электрическая емкость не зависит от заряда проводника, а определяется его геометрическими размерами и формой, расположением относительно других проводников и электрическими свойствами окружающей среды. · Емкостью конденсатора называется физическая величина, равная
Электрическая емкость плоского конденсатора
· Заряженный конденсатор обладает энергией
· Энергия конденсатора сосредоточена в электрическом поле. Объемная плотность энергии электростатического поля определяется следующим образом:
Вопросы для самоконтроля и повторения 1. Что представляет собой электрическое поле, и какими свойствами 2. Что такое электрический заряд? Какой электрический заряд называют точечным? 3. Сформулируйте закон сохранения электрического заряда. 4. Сформулируйте закон Кулона. 5. Что называют напряженностью электрического поля? Какое поле 6. Что называют циркуляцией вектора напряженности электростати-ческого поля? 7. Что является энергетической характеристикой электрического поля? Как связаны между собой напряженность и потенциал электростатического поля? 8. Сформулируйте теорему Гаусса для электростатического поля в вакууме. С какой целью она применяется? 9. Какие вещества называют диэлектриками? В чем состоит явление 10. Что характеризует электрическая емкость проводника, от чего она 11. Что представляет собой конденсатор? Из каких соображений выбирается геометрия его обкладок? Как рассчитывается емкость батареи 12. Как определяется энергия уединенного проводника, заряженного конденсатора? Примеры решения задач
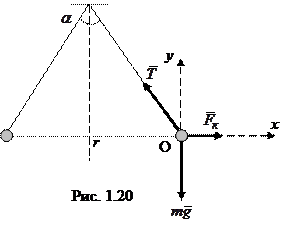
Дано: Решение Условие равновесия шариков имеет вид (рис. 1.20):
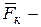 кулоновская сила, кулоновская сила,  сила натяжения нити. В проекциях на оси Оx и Оy это условие примет вид: сила натяжения нити. В проекциях на оси Оx и Оy это условие примет вид:
откуда
где Искомый заряд Подставляя числовые данные, получим Ответ:
Дано: Найти: Решение Напряженность результирующего поля в точке А равна векторной сумме напряженностей полей, создаваемых зарядами
где
Подставляя исходные числовые данные в указанные формулы, получим Потенциал
где
Потенциал
Ответ:
Задача 3. На металлической сфере радиусом 15см находится заряд 2 нКл. Определить напряженность электростатического поля: Дано:
Найти: Решение Согласно теореме Гаусса, Тогда:
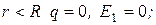
б) при в) при Подставляя числовые данные, получим Ответ:
Задача 4. Определить эквивалентную емкость Дано: Найти: Решение В задачах подобного типа можно использовать метод, связанный с определением точек цепи,
Найдем эквивалентную емкость цепи двумя способами: а) согласно схеме (рис. 1.24, а),
откуда
б) согласно схеме (рис. 1.24, б),
Ответ:
Задачи для самостоятельного решения 1. Расстояние между зарядами 2. Расстояние между зарядами 3. Электрический диполь образован двумя равными по величине и противоположными по знаку зарядами 4. Определить модуль и направление силы F взаимодействия положительного заряда Q и диполя с плечом d. Заряд Q находится в точке, расположенной на одинаковом расстоянии r от каждого из зарядов диполя. 5. В трех вершинах квадрата со стороной а находятся одинаковые положительные заряды q. Найти напряженность электрического поля в четвертой вершине. (Ответ: 6. Два одинаковых одноименно заряженных шарика, подвешенные на нитях одинаковой длины, опускают в жидкий диэлектрик, плотность которого 7. На шероховатой горизонтальной поверхности закреплен заряд q 1. Тело массой m, имеющее заряд q 2, может перемещаться по поверхности. На (Ответ: 8. Сосуд с маслом, диэлектрическая проницаемость которого 9. Шарик массой 10. Четыре одинаковые частицы, каждая из которых имеет массу 11. Шарик массой m = 2 г и зарядом 12. В плоском горизонтально расположенном конденсаторе находится 13. Поверхностная плотность заряда бесконечно протяженной вертикальной плоскости равна 14. Электростатическое поле создается сферой радиусом 5 см, равномерно заряженной с поверхностной плотностью 1 нКл/м2. Определить разность потенциалов между двумя точками поля, лежащими на расстояниях 15. Радиус центральной жилы коаксиального кабеля 1,5 см, радиус оболочки 3,5 см. Между центральной жилой и оболочкой приложена разность
17. Определить емкость батареи конденсаторов, изображенной на рис. 1.25. Емкость каждого 18. К пластинам плоского воздушного конденсатора приложена разность потенциалов 500 В. Площадь пластин 200 см2, расстояние между ними
(Ответ: 1) 2)
19. Емкость батареи одинаковых конденсаторов равна 2/3 С, где С – емкость одного конденсатора. Какому из приведенных соединений конденсаторов (рис. 1.26) это соответствует? (Ответ: 4).
|
|||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 530; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.111.44 (0.009 с.) |

 ,
,  и
и  . Увеличим заряд этого проводника на
. Увеличим заряд этого проводника на 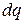 . Это связано с совершением работы по преодолению кулоновских сил отталкивания между одноименными зарядами. Совершаемая работа идет на увеличение электрической энергии заряженного проводника. Следовательно, элементарная работа
. Это связано с совершением работы по преодолению кулоновских сил отталкивания между одноименными зарядами. Совершаемая работа идет на увеличение электрической энергии заряженного проводника. Следовательно, элементарная работа 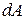 , совершаемая внешними силами при переносе малого заряда
, совершаемая внешними силами при переносе малого заряда 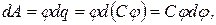
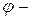 потенциал проводника, начало отсчета которого выбрано в бесконечно удаленной точке.
потенциал проводника, начало отсчета которого выбрано в бесконечно удаленной точке.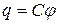 , равна
, равна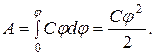 (1.45)
(1.45) (1.46)
(1.46) заряд конденсатора, а
заряд конденсатора, а 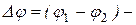 разность потенциалов между его обкладками,
разность потенциалов между его обкладками, 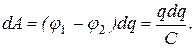
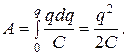
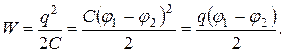 (1.47)
(1.47) и
и 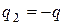 , формулу (1.47) можно переписать
, формулу (1.47) можно переписать 
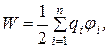 (1.48)
(1.48) заряд i -проводника;
заряд i -проводника;  потенциал, создаваемый в той точке, где находится заряд
потенциал, создаваемый в той точке, где находится заряд  , всеми зарядами, кроме i -го.
, всеми зарядами, кроме i -го.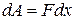 за счет уменьшения потенциальной энергии системы
за счет уменьшения потенциальной энергии системы
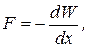
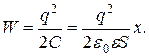
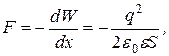
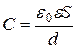 и
и 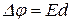 . Тогда получим формулу, связывающую энергию электростатического поля плоского конденсатора с напряженностью
. Тогда получим формулу, связывающую энергию электростатического поля плоского конденсатора с напряженностью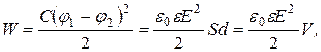 (1.49)
(1.49) объем конденсатора.
объем конденсатора.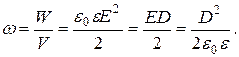 (1.50)
(1.50)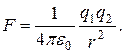

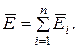

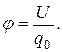
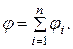




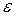 раз:
раз:
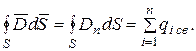
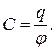

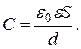
 Задача 1. Два шарика массой по 1г каждый подвешены на нитях, верхние концы которых соединены вместе. Длина каждой нити 10см. Какие одинаковые заряды надо сообщить шарикам, чтобы нити разошлись на угол 600?
Задача 1. Два шарика массой по 1г каждый подвешены на нитях, верхние концы которых соединены вместе. Длина каждой нити 10см. Какие одинаковые заряды надо сообщить шарикам, чтобы нити разошлись на угол 600?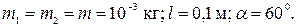
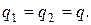


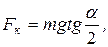 или
или 
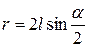 .
.
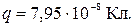
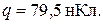
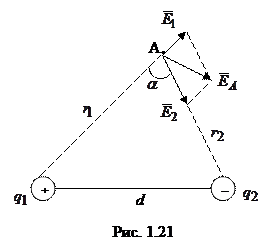 Задача 2. Два точечных электрических заряда
Задача 2. Два точечных электрических заряда 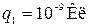
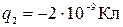 находятся в воздухе на расстоянии
находятся в воздухе на расстоянии  друг от друга. Определить напряженность и потенциал поля, создаваемого этими зарядами в точке А
друг от друга. Определить напряженность и потенциал поля, создаваемого этими зарядами в точке А 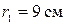 и
и  .
.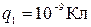 ;
;  ;
; 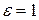 .
.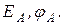
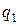 и
и 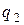 , то есть
, то есть
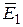 направлен от заряда
направлен от заряда 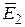 направлен в сторону заряда
направлен в сторону заряда 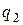 , так как этот заряд отрицательный. Вектор
, так как этот заряд отрицательный. Вектор  напряженности результирующего поля определяется как геометрическая сумма
напряженности результирующего поля определяется как геометрическая сумма 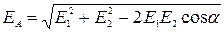 ,
,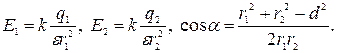
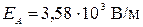 .
.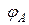 результирующего поля, созданного двумя зарядами
результирующего поля, созданного двумя зарядами 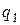
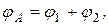
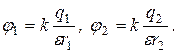
 является положительным, так как поле создано положительным зарядом
является положительным, так как поле создано положительным зарядом 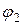 является отрицательным, так как поле создано отрицательным зарядом
является отрицательным, так как поле создано отрицательным зарядом 



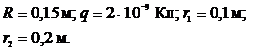
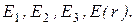
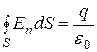 .
. откуда
откуда 
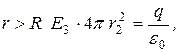 откуда
откуда 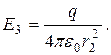
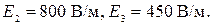
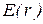 приведен на рис. 1.22.
приведен на рис. 1.22.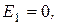


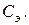
 В заданной схеме вследствие симметрии и равенства емкостей пар конденсаторов
В заданной схеме вследствие симметрии и равенства емкостей пар конденсаторов  поэтому
поэтому 
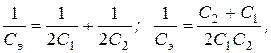
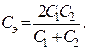
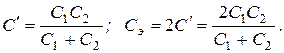

 и
и 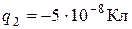 равно 10см. Определить силу, действующую на заряд
равно 10см. Определить силу, действующую на заряд  , отстоящий на 12см от заряда
, отстоящий на 12см от заряда 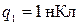 и
и  равно 55 см. Определить напряженность поля в точке, потенциал в которой равен нулю, если точка лежит на прямой, проходящей через заряды. (Ответ: 3960В/м
равно 55 см. Определить напряженность поля в точке, потенциал в которой равен нулю, если точка лежит на прямой, проходящей через заряды. (Ответ: 3960В/м 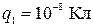 и
и 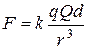 ).
).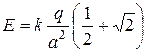 ).
). и диэлектрическая проницаемость
и диэлектрическая проницаемость  материала шариков, чтобы углы расхождения нитей в воздухе
материала шариков, чтобы углы расхождения нитей в воздухе 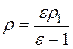 ).
). ).
).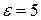 ,
,  , имеющий заряд
, имеющий заряд  Определить напряженность внешнего электрического поля Е, если плотность алюминия
Определить напряженность внешнего электрического поля Е, если плотность алюминия  , плотность масла
, плотность масла  . (Ответ:
. (Ответ: 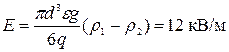 ).
).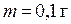 , несущий заряд
, несущий заряд 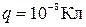 , подвешен в поле тяжести на нити длиной
, подвешен в поле тяжести на нити длиной 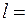 3 см. Над точкой подвеса на расстоянии
3 см. Над точкой подвеса на расстоянии 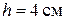 от нее помещен заряд
от нее помещен заряд 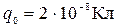 . Шарик с нитью отклоняют от положения равновесия на угол
. Шарик с нитью отклоняют от положения равновесия на угол  и отпускают. Найти скорость шарика при прохождении им положения равновесия. (Ответ: 0,89м/с).
и отпускают. Найти скорость шарика при прохождении им положения равновесия. (Ответ: 0,89м/с). и заряд
и заряд  , поместили на горизонтальную поверхность в вершинах квадрата со стороной
, поместили на горизонтальную поверхность в вершинах квадрата со стороной 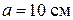 . Затем частицы одновременно освободили, после чего они стали симметрично разлетаться под действием кулоновских сил. Определить максимальные скорости частиц. (Ответ: 0,11м/с).
. Затем частицы одновременно освободили, после чего они стали симметрично разлетаться под действием кулоновских сил. Определить максимальные скорости частиц. (Ответ: 0,11м/с).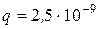 Кл подвешен на нити
Кл подвешен на нити  рад/с. В центре окружности поместили шарик с таким же зарядом. Какой должна стать угловая скорость вращения шарика, чтобы радиус окружности не изменился? Принять g= 10 м/с. (Ответ:
рад/с. В центре окружности поместили шарик с таким же зарядом. Какой должна стать угловая скорость вращения шарика, чтобы радиус окружности не изменился? Принять g= 10 м/с. (Ответ:  рад/с).
рад/с).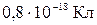 . Определить радиус капли. Плотность ртути 13600 кг/м3. (Ответ: 0,44 мкм).
. Определить радиус капли. Плотность ртути 13600 кг/м3. (Ответ: 0,44 мкм).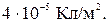 К плоскости на нити подвешен одноименно заряженный шарик массой 1 г и зарядом 1 нКл. Какой угол
К плоскости на нити подвешен одноименно заряженный шарик массой 1 г и зарядом 1 нКл. Какой угол 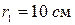 и
и  от центра сферы. (Ответ:
от центра сферы. (Ответ: 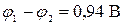 ).
).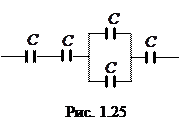 16. Два конденсатора емкостью соответственно
16. Два конденсатора емкостью соответственно  и
и 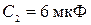 соединены последовательно. Разность потенциалов на зажимах этой батареи 9 В. Определить заряды
соединены последовательно. Разность потенциалов на зажимах этой батареи 9 В. Определить заряды 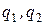 и разность потенциалов на обкладках каждого конденсатора. (Ответ:
и разность потенциалов на обкладках каждого конденсатора. (Ответ: 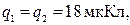
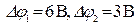 ).
).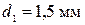 . Пластины раздвинули до расстояния
. Пластины раздвинули до расстояния 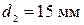 . Найти энергию конденсатора до и после раздвижения пластин, если источник напряжения перед раздвижением: 1) отключался; 2) не отключался.
. Найти энергию конденсатора до и после раздвижения пластин, если источник напряжения перед раздвижением: 1) отключался; 2) не отключался. ;
; ).
).



