VII.1. Краткая история развития представлений
О природе света
Оптика – раздел физической науки, в котором рассматриваются закономерности излучения, распространения и поглощения света. Традиционно оптику принято подразделять на геометрическую и физическую.
Геометрическая (лучевая) оптика не изучает природу света. Ее основными законами являются прямолинейное распространение света в прозрачных средах, его отражение и преломление. При этом свет рассматривается как совокупность световых лучей – линий, вдоль которых распространяется энергия.
Физическая оптика изучает вопросы, связанные с природой света и оптических явлений. Природа света двойственна. С одной стороны, свет представляет собой электромагнитную волну, с другой – поток частиц (фотонов). В связи с этим различают волновую и квантовую оптику.
Волновая оптика рассматривает оптические явления, в которых проявляется волновая природа света – явления интерференции, дифракции, поляризации и дисперсии. В основе волновой оптики лежат уравнения Максвелла
и вытекающие из них соотношения для электромагнитных волн. Максвелл писал: «Едва ли мы можем избежать заключения, что свет – это поперечное волнообразное движение той же самой природы, которая вызывает электрические и магнитные явления».
Оптика – одна из древнейших наук, тесно связанная с потребностями практики на протяжении всего своего развития. Прямолинейность распространения света была известна народам Месопотамии за 5 тысяч лет до
нашей эры. Пифагор (VI в. до н.э.) высказал близкую к современной точку зрения, что тела становятся видимыми благодаря испускаемым ими
частицами. Аристотель (IV в. до н.э.) полагал, что свет представляет собой возбуждение среды, находящейся между объектом и глазом. В том же веке
в школе Платона были сформулированы два важнейших закона геометри-ческой оптики – прямолинейность лучей света и равенство углов их падения и отражения.
Следующий важный шаг развития оптики состоял в понимании законов преломления света и был сделан лишь много веков спустя. В средние века хорошо были известны эмпирические правила построения изображений,
даваемые линзами, и начало развиваться искусство изготовления линз.
В XIII в. появились очки. В 1590 г. нидерландский ученый З. Янсен построил первый двухлинзовый микроскоп. В 1609 г. Г. Галилей создал телескоп,
с помощью которого первые же наблюдения привели к ряду замечательных астрономических открытий. Однако точные законы преломления света были экспериментально установлены лишь в 20-х годах XVII в. голландским
ученым В. Снеллем и французским ученым Р. Декартом. Их работами был завершен фундамент построения геометрической оптики.
С конца XVII в. в оптике развернулась борьба между корпускулярной
и волновой теориями света. Автор первой теории – И. Ньютон – считал свет потоком корпускул (частиц), выбрасываемых светящимся телом и летящих в пространстве прямолинейно. С этим представлением хорошо согласовывались закон прямолинейного распространения света и закон отражения. Теория Ньютона объяснила и закон преломления света, причем из нее
следовало, что в более плотной среде свет распространяется с большей
скоростью, чем в менее плотной.
Волновую теорию света предложил современник Ньютона голландский ученый Х. Гюйгенс. Следуя идеям Леонардо да Винчи и развивая работы
Ф. Гримальди и Р. Гука, Гюйгенс исходил из аналогии между многими
акустическими и оптическими явлениями. Он полагал, что световое возбуждение есть импульсы упругих колебаний особой среды – эфира, распространяющиеся с большой, но конечной скоростью. Наибольшим вкладом Гюйгенса в оптику является установление принципа, согласно которому каждая точка волнового фронта может рассматриваться как источник вторичных
(сферических) волн.
Гюйгенс дал волновое истолкование законов отражения и преломления, причем из его теории следовало правильное выражение для показателя
преломления  (где (где 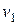 и и  – скорости света в 1-й и 2-й средах). Однако, сформулировав фундаментальный принцип волновой оптики, Гюйгенс не разработал последовательную волновую теорию света, которая могла бы противостоять воззрениям Ньютона. Поэтому корпускулярная «теория – скорости света в 1-й и 2-й средах). Однако, сформулировав фундаментальный принцип волновой оптики, Гюйгенс не разработал последовательную волновую теорию света, которая могла бы противостоять воззрениям Ньютона. Поэтому корпускулярная «теория
истечения» сохраняла господствующее положение в оптике до начала XIX в.
Победа волновой теории света связана с работами Т. Юнга и О. Френеля. В 1801 г. Юнг сформулировал принцип интерференции, позволивший ему объяснить цвета тонких пленок и послуживший основой для понимания всех интерференционных явлений. Френель, используя принцип Гюйгенса, дал волновую интерпретацию прямолинейности распространения света
и объяснил многочисленные дифракционные явления. В опытах Френеля
и Д. Араго было установлено, что волны, поляризованные перпендикулярно друг другу, не интерферируют. Это дало основание Юнгу и Френелю высказать важную идею о поперечности световых колебаний. Таким образом, все известные к тому времени оптические явления получили волновую интерпретацию.
Вместе с тем представление о свете как упругих поперечных колебаний эфира приводила к необходимости искусственных теоретических построений (эфир приходилось наделять свойствами твердого состояния и в то же время допускать, что в нем могут свободно перемещаться тела). Эти трудности были разрешены лишь после создания Д. Максвеллом учения об электромагнитном поле.
Первое указание на непосредственную связь электромагнетизма с оптикой было сделано М. Фарадеем в 1848 г. Последующие теоретические
исследования Максвелла (1865) показали, что изменения электрического
и магнитного полей не локализованы в пространстве, а распространяются со скоростью, равной скорости света. Это теоретическое заключение позднее было подтверждено опытами Г. Герца (1887). По Максвеллу свет – электромагнитная волна, распространяющаяся в среде со скоростью
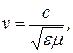
где с – скорость света в вакууме;  – соответственно относительная – соответственно относительная
диэлектрическая и относительная магнитная проницаемости среды. При этом показатель преломления среды

Это соотношение связывает оптические, электрические и магнитные
характеристики вещества. Однако из него не следует зависимость показателя преломления вещества от длины световой волны, хотя опыты показывают, что такая зависимость существует (дисперсия света). Теория Максвелла
не могла объяснить этого явления. Это было сделано Г. Лоренцем (1896), создавшим электронную теорию света.
Электромагнитная теория света не только объясняла наблюдаемые
оптические явления, но и позволила предсказать такое явление, как давление света, которое экспериментально было обнаружено в 1899 г. русским
ученым П.Н. Лебедевым. По этому поводу английский физик Д. Томсон писал: «Я всю свою жизнь воевал с Максвеллом, не признавая его светового давления, а вот опыты Лебедева заставили меня сдаться». Таким образом, свет – это электромагнитные волны, которые могут распространяться как
в среде, так и в вакууме.
Несмотря на успехи классической электродинамической теории света Максвелла-Лоренца, вскоре выяснилось, что она недостаточна для описания процессов поглощения и испускания света. Особенно отчетливо это проявилось в парадоксальности выводов теории (противоречащих закону сохранения энергии) из анализа распределения по длинам волн излучения абсолютно черного тела. Рассматривая эту принципиальную проблему, немецкий физик М. Планк пришел к заключению (1900), что элементарная колебательная система (атом, молекула) отдает энергию электромагнитному полю
не непрерывно, а дискретно, отдельными порциями или квантами, пропорциональными частоте колебаний. Развитие идеи Планка, противоречащей классическим представлениям, не только дало удовлетворительное решение проблемы теплового излучения, но и заложило основы современной квантовой физики. Работы Планка и А. Эйнштейна (1905), который приписал квантам света – фотонам, кроме энергии, также импульс и массу, вернули оптике многие черты корпускулярных представлений. Квантовую теорию света
в дальнейшем развивали в своих трудах Н. Бор, М. Борн, В. Гейзенберг,
В. Паули, Э. Шрёдингер, П. Дирак, Э. Ферми, Л.Д. Ландау и другие
выдающиеся ученые-физики.
Таким образом, на основании современных представлений свет имеет двойственную корпускулярно-волновую природу (корпускулярно-волновой дуализм): с одной стороны, он обладает волновыми свойствами (явления
интерференции, дифракции, поляризации), с другой – представляет собой поток частиц – фотонов, обладающих нулевой массой покоя и движущихся со скоростью, равной скорости света в вакууме.
Корпускулярно-волновой дуализм есть проявление наиболее общей взаимосвязи двух основных форм существования материи – вещества и поля.
VII.2. Интерференция света
Поскольку свет – разновидность электромагнитных волн, должно
наблюдаться явление интерференции света – устойчивое чередование максимумов и минимумов освещенности при наложении двух или нескольких когерентных световых волн. Такие проявления интерференции света, как переливы тонкой пленки масла на поверхности воды, радужные цвета
мыльных пленок – люди наблюдали давно, но не могли дать им объяснения.
 Первым объяснил явление интерференции света английский ученый Первым объяснил явление интерференции света английский ученый
Т. Юнг (1773-1829), наблюдая отражение и преломление световых волн
в тонких пленках (рис. 7.1). Белый свет, падая на тонкую пленку, частично (волна 1) отражается от верхней поверхности пленки, частично (волна 2), пройдя через пленку, отражается от ее нижней
поверхности. Обе отраженные волны ( и и  ) )
отличаются оптической длиной пути (больший путь проходит волна, отраженная от нижней
поверхности пленки). При этом происходит наложение этих волн, результат которого зависит
от угла падения света на пленку, ее толщины,
показателя преломления n вещества и длины
волны  . Усиление света происходит, когда преломленная волна . Усиление света происходит, когда преломленная волна  отстает от отраженной волны отстает от отраженной волны  на целое число длин волн на целое число длин волн

где D – оптическая разность хода волн.
Также Т. Юнг понял, что различие в цвете связано с различием в длине волны. Другими словами, вне нас в природе нет никаких красок (цветов) – есть лишь электромагнитные волны разной длины (белый свет немонохроматичен, он содержит электромагнитные волны разной длины – от 400 до 760нм). Человеческий глаз – это оптический прибор, способный
фиксировать различия в длинах световых волн, то есть обнаруживать разницу
в цвете. Из-за того, что D зависит от длины волны, максимумы интерференционной картины для разных длин волн получаются в разных точках сетчатки глаза. Именно поэтому тонкие пленки имеют радужную окраску.
Необходимым условием интерференции волн является их когерентность – постоянство во времени разности фаз накладываемых волн. Этому условию удовлетворяют монохроматические волны, то есть волны строго определенной частоты (длины волны) и постоянной амплитуды. Однако
ни один реальный источник не дает строго монохроматического света.
Поэтому волны, излучаемые любыми независимыми источниками света
(например, несколькими электрическими лампочками), всегда некогерентные. Чтобы понять это, необходимо обратить внимание на механизм излучения света атомами вещества.
 Излучение светящегося тела скла-дывается из волн, испускаемых отдельными атомами. Продолжительность Излучение светящегося тела скла-дывается из волн, испускаемых отдельными атомами. Продолжительность
излучения отдельного возбужденного атома составляет около  с. За это время в вакууме образуется волновой цуг – обрывок синусоиды (рис. 7.2), протяженность которого равна примерно с. За это время в вакууме образуется волновой цуг – обрывок синусоиды (рис. 7.2), протяженность которого равна примерно

Так как свет излучается одновременно огромным количеством атомов, и излучают они независимо друг от друга (хаотически во времени), то реальная световая волна представляет собой набор (пакет) волновых цугов с беспо-рядочно меняющейся фазой. Таким образом, в уравнении электромагнитной волны

фаза является случайной функцией времени. Волны, фазы которых меняются случайно и независимо друг от друга, называются некогерентными.
Наиболее распространенным способом получения когерентных волн от обычных источников (не лазеров) является искусственное разделение световой волны, излучаемой одним источником, на две составные части, которые
после прохождения различных оптических путей накладываются друг на друга и создают интерференционную картину. Реализовать этот способ можно с помощью различных приборов: зеркал Френеля, бипризмы Френеля, щелей Юнга и др. На рис. 7.3 приведена схема интерференционной установки Т. Юнга, которая была использована им для измерения длины световой
волны (1803).

Результат интерференции в точке М (максимум или минимум освещенности) на экране зависит от длины световой волны и разности хода волн от когерентных источников  и и  . Если в плоскости О фаза колебаний . Если в плоскости О фаза колебаний
исходной световой волны была 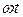 , то в точке М первая волна возбудит , то в точке М первая волна возбудит
колебание 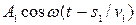 , вторая волна – колебание , вторая волна – колебание  , где , где  – фазовые скорости соответственно первой и второй волны, – фазовые скорости соответственно первой и второй волны, 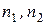 – показатели преломления сред, в которых распространяются волны. Разность фаз колебаний, возбуждаемых волнами в точке М, равна – показатели преломления сред, в которых распространяются волны. Разность фаз колебаний, возбуждаемых волнами в точке М, равна

где λ 0 – длина волны в вакууме; произведение геометрической длины пути s световой волны в данной среде на показатель преломления n этой среды
называется оптической длиной пути  ; ;  – оптическая – оптическая
разность хода.
Если оптическая разность хода равна целому числу длин волн в вакууме
 (7.1) (7.1)
то разность фаз колебаний  , и колебания, возбуждаемые обеими волнами в точке М, будут протекать в одинаковой фазе. Следовательно, (7.1) является условием интерференционного максимума. , и колебания, возбуждаемые обеими волнами в точке М, будут протекать в одинаковой фазе. Следовательно, (7.1) является условием интерференционного максимума.
Если оптическая разность хода волн
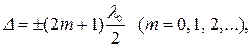 (7.2) (7.2)
то разность фаз колебаний  , и колебания, возбуждаемые , и колебания, возбуждаемые
волнами в точке М, будут происходить в противофазе. Следовательно, (7.2)
является условием интерференционного минимума.
Очевидно, что если точка М на экране равноудалена от когерентных
источников, то в ней образуется интерференционный максимум – светлая полоса: волны от  и и  придут в точку М с одинаковой фазой, оптическая разность хода придут в точку М с одинаковой фазой, оптическая разность хода  . Этот максимум называется нулевым или центральным. . Этот максимум называется нулевым или центральным.
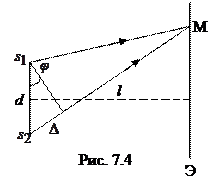 Если координата точки М на экране произвольная (рис. 7.4), то возникает разность хода интерферирующих волн Если координата точки М на экране произвольная (рис. 7.4), то возникает разность хода интерферирующих волн
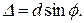
С другой стороны, условие интерференционного максимума 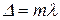 . Следовательно, если . Следовательно, если
выполняется условие
 , ,
то в точке М наблюдается светлая полоса, в противном случае – темная.
Таким образом, зная расстояние d между щелями, номер (порядок)
максимума m и угол  , под которым этот максимум наблюдается, можно определить длину , под которым этот максимум наблюдается, можно определить длину  световой волны. световой волны.
 Из вышеизложенного следует, что явление интерференции обусловлено волновой природой света. Поэтому это явление используется для определения длин световых волн, для весьма точного (порядка 10-7м) измерения размеров предметов, микронеровностей на поверхностях деталей, просветления оптики, определения показателя преломления прозрачных веществ. Рассмотрим некоторые применения интерференции. Из вышеизложенного следует, что явление интерференции обусловлено волновой природой света. Поэтому это явление используется для определения длин световых волн, для весьма точного (порядка 10-7м) измерения размеров предметов, микронеровностей на поверхностях деталей, просветления оптики, определения показателя преломления прозрачных веществ. Рассмотрим некоторые применения интерференции.
1. Для прецизионных измерений длин волн и размеров тел используются интерферометры. В качестве примера рассмотрим устройство и принцип работы интерферометра Майкельсона (рис. 7.5).
Монохроматический свет от источника S
падает под углом 450 на плоскопараллельную пластинку Р1, одна из сторон которой покрыта тонким слоем серебра и полупрозрачна. За счет этого в точке О исходный луч света
разделяется на две части: луч 1 (отражается от серебра) и луч 2 (проходит через слой серебра). Луч 1 отражается от зеркала М1 и, возвращаясь обратно, вновь проходит через пластинку Р1 (луч 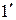 ). Луч 2 идет ). Луч 2 идет
к зеркалу М2, отражается от него, возвращается обратно и отражается
от пластинки Р1 (луч  ). Таким образом, зеркала М1 и М2 играют роль ). Таким образом, зеркала М1 и М2 играют роль
вторичных источников света, то есть обеспечивают условие когерентности лучей  и и  . .
Так как первый из лучей проходит пластинку Р1 дважды, то для компенсации возникающей разности хода на пути второго луча устанавливается пластинка Р2 (такая же, что и Р1, но без слоя серебра). Поэтому пластинку Р2 называют компенсатором.
Лучи  и и  когерентны, следовательно, будет наблюдаться интерференция, результат которой зависит от оптической разности хода луча 1 от точки О до зеркала М1 и обратно, и луча 2 от точки О до зеркала М2 когерентны, следовательно, будет наблюдаться интерференция, результат которой зависит от оптической разности хода луча 1 от точки О до зеркала М1 и обратно, и луча 2 от точки О до зеркала М2

где 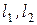 – расстояния от точки О до зеркал М1 и М2, n – абсолютный показатель преломления воздуха. – расстояния от точки О до зеркал М1 и М2, n – абсолютный показатель преломления воздуха.
Если  , то D = 0 и наблюдается интерференционный максимум. Смещение одного из зеркал (с помощью микрометрических винтов) на расстояние , то D = 0 и наблюдается интерференционный максимум. Смещение одного из зеркал (с помощью микрометрических винтов) на расстояние  приведет к появлению разности хода лучей приведет к появлению разности хода лучей

в результате чего возникнет интерференционный минимум:
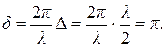
Таким образом, по незначительному смещению интерференционной картины можно судить о малом перемещении одного из зеркал и использовать интерферометр для точного измерения длины. Если поместить вместо одного из зеркал какую-либо деталь, можно по форме полос или колец
контролировать качество ее обработки.
 2. Особое место в применении интерференции занимает просветление оптики. При прохождении света через линзы или призмы от каждой из 2. Особое место в применении интерференции занимает просветление оптики. При прохождении света через линзы или призмы от каждой из
поверхностей световой поток частично отражается. В сложных оптических системах, где много различных линз (биноклях, фотоаппаратах, перископах, дальномерах и др.), проходящий световой поток вследствие отражения
может уменьшаться до 50% входящего в них света. Кроме того, отражения от поверхностей линз приводит к возникновению бликов. Для устранения этих
недостатков оптических приборов и применяется просветление оптики.
Сущность метода заключается в том, что поверхности линз покрываются тонкими пленками, создающими интерференционные явления (рис. 7.6). При этом накладываются когерентные световые лучи, отраженные от границ раздела воздух-пленка (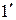 ) и пленка-стекло ( ) и пленка-стекло ( ). Толщину пленки d и показатели преломления стекла ). Толщину пленки d и показатели преломления стекла 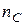 и пленки n можно подобрать так, чтобы интерферирующие в отраженном потоке лучи гасили друг друга. Обычно толщина просветляющего слоя составляет и пленки n можно подобрать так, чтобы интерферирующие в отраженном потоке лучи гасили друг друга. Обычно толщина просветляющего слоя составляет 
падающей световой волны. Тогда оптическая разность хода отраженных
лучей равна  , что соответствует условию минимума при интерференции. В результате достигается четкое изображение, и уничтожаются блики. , что соответствует условию минимума при интерференции. В результате достигается четкое изображение, и уничтожаются блики.
Добиться одновременного гашения в отраженном свете всех длин волн
невозможно, поэтому это делают для волн с  (наиболее восприимчивой глазом длины волны). В связи с этим объективы с просветленной (наиболее восприимчивой глазом длины волны). В связи с этим объективы с просветленной
оптикой имеют синевато-фиолетовый оттенок.
 Просветляющие покрытия наносятся на поверхности линз или призм Просветляющие покрытия наносятся на поверхности линз или призм
путем их химической обработки (травление в кислоте), нанесением пленок фторидов при испарении в вакууме или механически.
3. Для определения показателя преломления прозрачного вещества используются интерференционные рефрактометры (рис.7.7). На пути интерферирующих лучей помещаются две одинаковые кюветы 1 и 2 длиной l: одна заполнена газом с известным показателем преломления  , а другая – с неизвестным , а другая – с неизвестным  . В результате возникает оптическая разность хода лучей . В результате возникает оптическая разность хода лучей

которая приводит к сдвигу интерференционных полос на экране. Зная, на какую часть ширины интерференционной полосы m сместилась интерференционная картина, находят неизвестный показатель преломления вещества:


VII.3. Дифракция света
Дифракцией света называется явление отклонения света от прямолинейного направления при его распространении в среде с резко выраженной
оптической неоднородностью. Вследствие дифракции волны могут проникать через небольшие отверстия в экранах, огибать контуры непрозрачных предметов (попадать в область геометрической тени). Дифракцию можно наблюдать для волн любой природы, в том числе и механических (например, звук хорошо слышен за углом дома). Впервые явление дифракции
научно описал и дал ему название Ф. Гримальди (1618-1663).
Для наблюдения явления дифракции света необходимо выполнение специальных условий, так как масштабы этого явления сильно зависят от соотношения размеров препятствия и длины волны. При длине волны, сравнимой с размерами препятствия, дифракция выражена очень сильно; в случае, если  значительно меньше размеров препятствия, дифракция выражена слабо, то есть свет распространяется прямолинейно. значительно меньше размеров препятствия, дифракция выражена слабо, то есть свет распространяется прямолинейно.
Первым явление дифракции попытался объяснить Х. Гюйгенс, выдвинув в 1690 г. принцип построения волнового фронта (принцип Гюйгенса): каждая точка, до которой доходит волновое возмущение, служит центром вторичных волн, а огибающая этих волн дает положение волнового фронта в следующий момент времени (рис. 7.8). В качестве примера рассмотрим плоскую волну, падающую нормально на отверстие в непрозрачном экране (рис. 7.9). Каждая точка приходящегося на отверстие волнового фронта
является источником вторичной волны. Построив огибающую вторичных волн для некоторого момента времени, убедимся, что фронт волны заходит в область геометрической тени, то есть свет огибает края отверстия.

Однако принцип Гюйгенса не учитывает периодичность световых волн, что не позволяет объяснить структуру дифракционной картины. Он не затрагивает вопроса об амплитуде, а, следовательно, об интенсивности распространяющихся за препятствием световых волн.
В 1816 г. О. Френель сделал принцип Гюйгенса физически более содержательным, дополнив его положением об интерференции вторичных волн. Согласно принципу Гюйгенса-Френеля, волновое возмущение в любой точке пространства является результатом интерференции вторичных волн, излучаемых каждым элементом некоторой волновой поверхности.
Для того чтобы определить результат дифракции (амплитуду световых колебаний) в некоторой точке пространства, Френель предложил разбивать волновую поверхность на отдельные участки (зоны Френеля) так, чтобы волны, посылаемые двумя соседними зонами в данную точку, приходили
в противофазе. Таким образом, световые колебания, возбуждаемые
в данной точке пространства двумя соседними зонами, противоположны по фазе и при наложении должны взаимно ослаблять друг друга.
 Найдем в произвольной точке М амплитуду световой волны, распространяющейся в однородной среде от точечного источника S (рис. 7.10). Найдем в произвольной точке М амплитуду световой волны, распространяющейся в однородной среде от точечного источника S (рис. 7.10).
Согласно принципу Гюйгенса-Френеля заменим действие источника S действием
фиктивных (вторичных) источников, расположенных на волновой поверхности Ф (поверхности сферы радиуса  с центром S). Амплитуда волны в точке М определяется результатом интерференции волн от вторичных источников, то есть необходимо сложить когерентные колебания, возбуждаемые всеми фиктивными источниками на волновой поверхности. Так как расстояния от них до точки М различны, то колебания будут приходить в различных с центром S). Амплитуда волны в точке М определяется результатом интерференции волн от вторичных источников, то есть необходимо сложить когерентные колебания, возбуждаемые всеми фиктивными источниками на волновой поверхности. Так как расстояния от них до точки М различны, то колебания будут приходить в различных
фазах. Наименьшее расстояние от точки М до волновой поверхности равно b. Первая зона Френеля ограничивается точками волновой поверхности,
расстояния от которых до точки М равны  . Границы второй зоны Френеля определяются соотношением . Границы второй зоны Френеля определяются соотношением  и т. д. Так как колебания от соседних зон проходят до точки М расстояния, отличающиеся на и т. д. Так как колебания от соседних зон проходят до точки М расстояния, отличающиеся на  , то в точку М они приходят в противофазе, и наблюдается интерференционный минимум. Поэтому амплитуда результирующего колебания , то в точку М они приходят в противофазе, и наблюдается интерференционный минимум. Поэтому амплитуда результирующего колебания
в рассматриваемой точке
 (7.3) (7.3)
где  – амплитуды колебаний, возбуждаемых соответственно первой, второй, …, m -зонами. – амплитуды колебаний, возбуждаемых соответственно первой, второй, …, m -зонами.
Общее число зон Френеля, умещающихся на полусфере очень велико, поэтому приближенно можно считать, что амплитуда  колебаний от колебаний от
некоторой m-й зоны Френеля равна среднему арифметическому от амплитуд примыкающих к ней зон 
Тогда выражение (7.3) можно записать в виде

 (7.4) (7.4)
Полученный результат показывает, что амплитуда результирующего светового колебания определяется действием только половины центральной зоны Френеля (все остальные вторичные волны гасятся в результате интерференции). Следовательно, распространение света от источника S к точке М происходит так, будто световой поток распространяется внутри очень узкого канала вдоль SM, то есть прямолинейно. Таким образом, принцип Гюйгенса-Френеля позволяет объяснить прямолинейное распространение света
в однородной среде.
Поместим теперь на пути сферической волны, распространяющейся от точечного источника S, препятствие в виде непрозрачной пластины с круглым отверстием (дифракция на круглом отверстии). Для наблюдения дифрак-ционной картины параллельно плоскости отверстия на расстоянии b
расположен экран (рис. 7.11).
 Разобьем открытую часть волновой поверхности на зоны Френеля. Вид дифракционной картины зависит от числа зон Френеля, укладывающихся на ширине отверстия. Амплитуда результирующего светового колебания, возбуждаемого в точке М всеми зонами Разобьем открытую часть волновой поверхности на зоны Френеля. Вид дифракционной картины зависит от числа зон Френеля, укладывающихся на ширине отверстия. Амплитуда результирующего светового колебания, возбуждаемого в точке М всеми зонами 
где знак «плюс» соответствует нечетному числу m зон Френеля, знак «минус» – четному числу зон Френеля.
Когда отверстие открывает нечетное число зон
Френеля, то амплитуда результирующего колебания (интенсивность света) в точке М будет больше, чем при свободном распространении волны, если четное – то амплитуда будет равна нулю. Если в отверстие укладывается одна зона Френеля, то в точке М
амплитуда 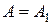 , то есть вдвое больше, чем при отсутствии препятствия [см. формулу (7.4)]. Таким образом, дифракционная картина от круглого , то есть вдвое больше, чем при отсутствии препятствия [см. формулу (7.4)]. Таким образом, дифракционная картина от круглого
отверстия вблизи точки М будет иметь вид чередующихся темных и светлых колец с центрами в точке М: если m четное, то в центре будет темное кольцо, если m нечетное – светлое кольцо, причем интенсивность убывает с увеличением расстояния от центра картины.
Дифракция на щели плоских световых волн. Пусть на узкую щель шириной 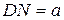 , расположенную в непрозрачной преграде, нормально падает , расположенную в непрозрачной преграде, нормально падает
плоская монохроматическая световая волна (рис. 7.12). За щелью помещена собирающая линза, в фокальной плоскости которой расположен экран для наблюдения дифракционной картины.
По принципу Гюйгенса-Френеля освещенная щель является источником вторичных световых когерентных волн, распространяющихся по всем
направлениям и способных интерферировать друг с другом.
Рассмотрим направление, параллельное главной оптической оси линзы Л и совпадающее с направлением падающей волны ( ). Линза соберет ). Линза соберет
световые лучи этого направления в своем главном фокусе F. Все эти лучи до точки F проходят одинаковые оптические пути, поэтому в нее они придут
в одинаковой фазе и, интерферируя, усилят друг друга. Следовательно,
в главном фокусе линзы всегда наблюдается максимум интенсивности I
света, который имеет вид ярко освещенной полосы, параллельной щели.
 Рассмотрим теперь лучи, идущие под углом Рассмотрим теперь лучи, идущие под углом  к первоначальному к первоначальному
направлению распространения волны. Эти лучи линза соберет в точке М. Чтобы узнать, каков результат интерференции вторичных волн в данном случае, сделаем следующие построения. Проведем перпендикуляр DC
к направлению распространения вторичных волн. Тогда оптическая разность хода между лучами, идущими от крайних точечных источников D и N, равна 
Далее воспользуемся методом зон Френеля. Для определения числа зон Френеля на участке  разобьем его на отрезки, равные половине длины волны λ /2, и через точки разбиений проведем плоскости, параллельные DC. Эти плоскости разделят щель разобьем его на отрезки, равные половине длины волны λ /2, и через точки разбиений проведем плоскости, параллельные DC. Эти плоскости разделят щель
на зоны Френеля, которые в данном случае представляют собой полоски, параллельные краям щели.
Число зон, укладывающихся в щели, зависит от длины волны и угла  ( ( ). В свою очередь, от числа зон Френеля зависит результат наложения всех вторичных волн. Если число зон Френеля четное, то есть выполняется условие ). В свою очередь, от числа зон Френеля зависит результат наложения всех вторичных волн. Если число зон Френеля четное, то есть выполняется условие
 (7.5) (7.5)
то в точке М наблюдается дифракционный минимум (вторичные волны, идущие от двух соседних зон, погасят друг друга).
В направлениях, которым соответствует нечетное число зон Френеля, укладывающихся в щели, то есть при выполнении условия
 (7.6) (7.6)
наблюдается дифракционный максимум, обусловленный действием одной некомпенсированной зоны Френеля.
Из условий (7.5) и (7.6) можно найти направления лучей на точки экрана, в которых интенсивность света равна нулю
 (7.7) (7.7)
или максимальна
 (7.8) (7.8)
Распределение интенсивности на экране, получаемое вследствие
дифракции, называют дифракционным спектром. При неизменной ширине щели максимумы интенсивности света различной длины волны приходятся на различные углы. Если щель освещать белым светом, то центральный
(нулевой) максимум будет белым, а по обе стороны от него расположатся цветные максимумы первого порядка: согласно (7.8) красный свет ( ) отклонится на больший угол, чем фиолетовый ( ) отклонится на больший угол, чем фиолетовый ( ). Между ними расположатся остальные цвета спектра. ). Между ними расположатся остальные цвета спектра.
Дифракционная решетка. Использование дифракции света на одной
щели затруднено из-за слабой видимости дифракционной картины. Поэтому
в практических целях применяется специальное устройство – дифракционная решетка.
Дифракционная решетка – спектральный прибор, предназначенный для разложения света в спектр и измерения длины световой волны. Простейшая одномерная решетка представляет собой совокупность большого числа
регулярно расположенных препятствий и щелей на металлической или
стеклянной пластинке (лучшие металлические решетки имеют до 2000 штрихов на один миллиметр поверхности, общая длина решетки составляет 100-150мм).
Если ширина каждой щели равна а, а ширина непрозрачных участков между щелями b, то величина  называется периодом или постоянной дифракционной решетки. называется периодом или постоянной дифракционной решетки.
 Дифракционная картина на решетке определяется как результат интерференции волн, идущих от всех щелей (многолучевая интерференция света). Дифракционная картина на решетке определяется как результат интерференции волн, идущих от всех щелей (многолучевая интерференция света).
Пусть плоская монохроматическая волна падает нормально плоскости решетки (рис. 7.13). Так как щели находятся друг от друга на одинаковых расстояниях, то разность хода лучей,
идущих от двух соседних щелей, будет для данного направления  одинакова в пределах всей дифракционной решетки: одинакова в пределах всей дифракционной решетки:

В направлениях (то есть для таких углов φ), в которых световые волны ни от одной из щелей не распространяются (свет от разных частей каждой щели полностью гасится в результате интерференции), они не будут распространяться и при N щелях. Следовательно, главные минимумы интенсивности будут наблюдаться в направлениях, для которых выполняется условие (7.5):

Вследствие взаимной интерференции волн действие одной щели будет усиливать действие другой, если
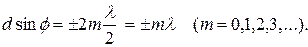 (7.9) (7.9)
Соотношение (7.9) выражает условие главных максимумов.
Кроме главных максимумов имеется большое число очень слабых
побочных максимумов, разделенных дополнительными минимумами. Условие дополнительных минимумов имеет вид
 (7.10) (7.10)
где р= 1, 2, 3,…, кроме N, 2 N, 3 N и т.д.; N – число штрихов решетки.
Таким образом,
|




 (где
(где 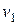 и
и  – скорости света в 1-й и 2-й средах). Однако, сформулировав фундаментальный принцип волновой оптики, Гюйгенс не разработал последовательную волновую теорию света, которая могла бы противостоять воззрениям Ньютона. Поэтому корпускулярная «теория
– скорости света в 1-й и 2-й средах). Однако, сформулировав фундаментальный принцип волновой оптики, Гюйгенс не разработал последовательную волновую теорию света, которая могла бы противостоять воззрениям Ньютона. Поэтому корпускулярная «теория 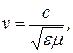
 – соответственно относительная
– соответственно относительная 
 Первым объяснил явление интерференции света английский ученый
Первым объяснил явление интерференции света английский ученый  и
и  )
)  . Усиление света происходит, когда преломленная волна
. Усиление света происходит, когда преломленная волна 
 Излучение светящегося тела скла-дывается из волн, испускаемых отдельными атомами. Продолжительность
Излучение светящегося тела скла-дывается из волн, испускаемых отдельными атомами. Продолжительность  с. За это время в вакууме образуется волновой цуг – обрывок синусоиды (рис. 7.2), протяженность которого равна примерно
с. За это время в вакууме образуется волновой цуг – обрывок синусоиды (рис. 7.2), протяженность которого равна примерно


 и
и  . Если в плоскости О фаза колебаний
. Если в плоскости О фаза колебаний 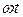 , то в точке М первая волна возбудит
, то в точке М первая волна возбудит 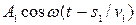 , вторая волна – колебание
, вторая волна – колебание  , где
, где  – фазовые скорости соответственно первой и второй волны,
– фазовые скорости соответственно первой и второй волны, 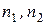 – показатели преломления сред, в которых распространяются волны. Разность фаз колебаний, возбуждаемых волнами в точке М, равна
– показатели преломления сред, в которых распространяются волны. Разность фаз колебаний, возбуждаемых волнами в точке М, равна
 ;
;  – оптическая
– оптическая  (7.1)
(7.1) , и колебания, возбуждаемые обеими волнами в точке М, будут протекать в одинаковой фазе. Следовательно, (7.1) является условием интерференционного максимума.
, и колебания, возбуждаемые обеими волнами в точке М, будут протекать в одинаковой фазе. Следовательно, (7.1) является условием интерференционного максимума.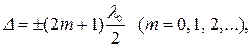 (7.2)
(7.2) , и колебания, возбуждаемые
, и колебания, возбуждаемые  . Этот максимум называется нулевым или центральным.
. Этот максимум называется нулевым или центральным.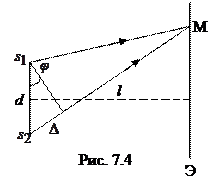 Если координата точки М на экране произвольная (рис. 7.4), то возникает разность хода интерферирующих волн
Если координата точки М на экране произвольная (рис. 7.4), то возникает разность хода интерферирующих волн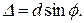
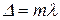 . Следовательно, если
. Следовательно, если  ,
, , под которым этот максимум наблюдается, можно определить длину
, под которым этот максимум наблюдается, можно определить длину  Из вышеизложенного следует, что явление интерференции обусловлено волновой природой света. Поэтому это явление используется для определения длин световых волн, для весьма точного (порядка 10-7м) измерения размеров предметов, микронеровностей на поверхностях деталей, просветления оптики, определения показателя преломления прозрачных веществ. Рассмотрим некоторые применения интерференции.
Из вышеизложенного следует, что явление интерференции обусловлено волновой природой света. Поэтому это явление используется для определения длин световых волн, для весьма точного (порядка 10-7м) измерения размеров предметов, микронеровностей на поверхностях деталей, просветления оптики, определения показателя преломления прозрачных веществ. Рассмотрим некоторые применения интерференции.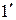 ). Луч 2 идет
). Луч 2 идет  и
и 
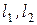 – расстояния от точки О до зеркал М1 и М2, n – абсолютный показатель преломления воздуха.
– расстояния от точки О до зеркал М1 и М2, n – абсолютный показатель преломления воздуха. , то D = 0 и наблюдается интерференционный максимум. Смещение одного из зеркал (с помощью микрометрических винтов) на расстояние
, то D = 0 и наблюдается интерференционный максимум. Смещение одного из зеркал (с помощью микрометрических винтов) на расстояние  приведет к появлению разности хода лучей
приведет к появлению разности хода лучей
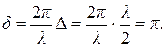
 2. Особое место в применении интерференции занимает просветление оптики. При прохождении света через линзы или призмы от каждой из
2. Особое место в применении интерференции занимает просветление оптики. При прохождении света через линзы или призмы от каждой из 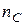 и пленки n можно подобрать так, чтобы интерферирующие в отраженном потоке лучи гасили друг друга. Обычно толщина просветляющего слоя составляет
и пленки n можно подобрать так, чтобы интерферирующие в отраженном потоке лучи гасили друг друга. Обычно толщина просветляющего слоя составляет 
 , что соответствует условию минимума при интерференции. В результате достигается четкое изображение, и уничтожаются блики.
, что соответствует условию минимума при интерференции. В результате достигается четкое изображение, и уничтожаются блики.  (наиболее восприимчивой глазом длины волны). В связи с этим объективы с просветленной
(наиболее восприимчивой глазом длины волны). В связи с этим объективы с просветленной  Просветляющие покрытия наносятся на поверхности линз или призм
Просветляющие покрытия наносятся на поверхности линз или призм  , а другая – с неизвестным
, а другая – с неизвестным  . В результате возникает оптическая разность хода лучей
. В результате возникает оптическая разность хода лучей


 Найдем в произвольной точке М амплитуду световой волны, распространяющейся в однородной среде от точечного источника S (рис. 7.10).
Найдем в произвольной точке М амплитуду световой волны, распространяющейся в однородной среде от точечного источника S (рис. 7.10).  с центром S). Амплитуда волны в точке М определяется результатом интерференции волн от вторичных источников, то есть необходимо сложить когерентные колебания, возбуждаемые всеми фиктивными источниками на волновой поверхности. Так как расстояния от них до точки М различны, то колебания будут приходить в различных
с центром S). Амплитуда волны в точке М определяется результатом интерференции волн от вторичных источников, то есть необходимо сложить когерентные колебания, возбуждаемые всеми фиктивными источниками на волновой поверхности. Так как расстояния от них до точки М различны, то колебания будут приходить в различных  . Границы второй зоны Френеля определяются соотношением
. Границы второй зоны Френеля определяются соотношением  и т. д. Так как колебания от соседних зон проходят до точки М расстояния, отличающиеся на
и т. д. Так как колебания от соседних зон проходят до точки М расстояния, отличающиеся на  (7.3)
(7.3) – амплитуды колебаний, возбуждаемых соответственно первой, второй, …, m -зонами.
– амплитуды колебаний, возбуждаемых соответственно первой, второй, …, m -зонами. колебаний от
колебаний от 

 (7.4)
(7.4) Разобьем открытую часть волновой поверхности на зоны Френеля. Вид дифракционной картины зависит от числа зон Френеля, укладывающихся на ширине отверстия. Амплитуда результирующего светового колебания, возбуждаемого в точке М всеми зонами
Разобьем открытую часть волновой поверхности на зоны Френеля. Вид дифракционной картины зависит от числа зон Френеля, укладывающихся на ширине отверстия. Амплитуда результирующего светового колебания, возбуждаемого в точке М всеми зонами 
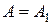 , то есть вдвое больше, чем при отсутствии препятствия [см. формулу (7.4)]. Таким образом, дифракционная картина от круглого
, то есть вдвое больше, чем при отсутствии препятствия [см. формулу (7.4)]. Таким образом, дифракционная картина от круглого 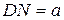 , расположенную в непрозрачной преграде, нормально падает
, расположенную в непрозрачной преграде, нормально падает  ). Линза соберет
). Линза соберет  Рассмотрим теперь лучи, идущие под углом
Рассмотрим теперь лучи, идущие под углом 
 разобьем его на отрезки, равные половине длины волны λ /2, и через точки разбиений проведем плоскости, параллельные DC. Эти плоскости разделят щель
разобьем его на отрезки, равные половине длины волны λ /2, и через точки разбиений проведем плоскости, параллельные DC. Эти плоскости разделят щель  ). В свою очередь, от числа зон Френеля зависит результат наложения всех вторичных волн. Если число зон Френеля четное, то есть выполняется условие
). В свою очередь, от числа зон Френеля зависит результат наложения всех вторичных волн. Если число зон Френеля четное, то есть выполняется условие (7.5)
(7.5) (7.6)
(7.6) (7.7)
(7.7) (7.8)
(7.8) ) отклонится на больший угол, чем фиолетовый (
) отклонится на больший угол, чем фиолетовый ( ). Между ними расположатся остальные цвета спектра.
). Между ними расположатся остальные цвета спектра. называется периодом или постоянной дифракционной решетки.
называется периодом или постоянной дифракционной решетки. Дифракционная картина на решетке определяется как результат интерференции волн, идущих от всех щелей (многолучевая интерференция света).
Дифракционная картина на решетке определяется как результат интерференции волн, идущих от всех щелей (многолучевая интерференция света).

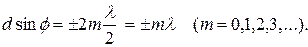 (7.9)
(7.9) (7.10)
(7.10)


