
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
VI.1. Свободные колебания в RLC-контуреСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Электромагнитными колебаниями называют периодические процессы, при которых происходят взаимосвязанные изменения электрических Для возбуждения и поддержания электромагнитных колебаний используется колебательный контур – электрическая цепь, состоящая из последовательно соединенных конденсатора емкостью С, катушки индуктивностью L и резистора сопротивлением R.
Рассмотрим колебательный процесс в идеализированном контуре, Так как
так как она не рассеивается на нагрев. Поэтому в момент В идеальном контуре ЭДС самоиндукции, возникающая при изменении тока, равна напряжению на обкладках конденсатора
Учитывая, что
Полученное дифференциальное уравнение аналогично рассмотренному в курсе механики уравнению
а период этих колебаний определяется формулой Томсона
Решением уравнения (6.1) является гармоническая функция
где По гармоническому закону изменяется не только заряд конденсатора,
Из выражений (6.4), (6.5) и (6.6) следует, что колебания заряда (напряжения) Уравнение (6.1) можно получить,
Учитывая, что

Так как в идеальном контуре
В реальном колебательном контуре (рис. 6.3)
или
Сравнивая это уравнение с дифференциальным уравнением свободных затухающих колебаний линейной системы
видим, что для электрического колебательного контура коэффициент затухания равен
Решение уравнения (6.7) имеет вид
где
Очевидно, что если Разделив зависимость
Зависимость силы тока в контуре от времени
Добротность колебательного контура
|
||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 408; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.72.24 (0.008 с.) |


 (рис. 6.1, а). Для возбуждения в контуре
(рис. 6.1, а). Для возбуждения в контуре  . Если замкнуть конденсатор на катушку индуктивности, он начнет разряжаться, и в контуре потечет возрастающий со временем ток i (рис. 6.1, б). В результате энергия электрического поля будет уменьшаться, а энергия магнитного поля катушки (
. Если замкнуть конденсатор на катушку индуктивности, он начнет разряжаться, и в контуре потечет возрастающий со временем ток i (рис. 6.1, б). В результате энергия электрического поля будет уменьшаться, а энергия магнитного поля катушки ( ) – возрастать.
) – возрастать.
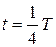 , когда
, когда  обращается в нуль, а заряд на обкладках конденсатора достигает максимума. Далее те же процессы начнут протекать в обратном направлении, и система к моменту времени
обращается в нуль, а заряд на обкладках конденсатора достигает максимума. Далее те же процессы начнут протекать в обратном направлении, и система к моменту времени  вернется к первоначальному состоянию. После этого рассмотренный цикл разрядки и зарядки конденсатора будет повторяться,
вернется к первоначальному состоянию. После этого рассмотренный цикл разрядки и зарядки конденсатора будет повторяться,  и тока, протекающего через катушку.
и тока, протекающего через катушку. , то есть
, то есть
 , получаем
, получаем (6.1)
(6.1) . Таким образом, свободные незатухающие колебания электрического заряда в идеальном контуре
. Таким образом, свободные незатухающие колебания электрического заряда в идеальном контуре  (6.2)
(6.2) (6.3)
(6.3) , (6.4)
, (6.4) – максимальный заряд на обкладках конденсатора.
– максимальный заряд на обкладках конденсатора. (6.5)
(6.5)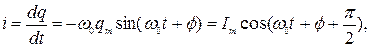 (6.6)
(6.6) где
где  – амплитуда напряжения на обкладках конденсатора,
– амплитуда напряжения на обкладках конденсатора,  – амплитуда силы тока в контуре.
– амплитуда силы тока в контуре. , то есть ток достигает максимального значения в те моменты времени, когда заряд (напряжение) на обкладках конденсатора равен нулю, и наоборот (рис. 6.2).
, то есть ток достигает максимального значения в те моменты времени, когда заряд (напряжение) на обкладках конденсатора равен нулю, и наоборот (рис. 6.2).
 , получим
, получим то
то  и, следовательно,
и, следовательно,
 , поэтому энергия колебаний будет
, поэтому энергия колебаний будет 
 (6.7)
(6.7)



 , как частный случай получаем циклическую частоту свободных незатухающих колебаний
, как частный случай получаем циклическую частоту свободных незатухающих колебаний 
 на величину емкости С конденсатора, получим закон изменения во времени напряжения на его обкладках:
на величину емкости С конденсатора, получим закон изменения во времени напряжения на его обкладках:
 .
.
 При увеличении сопротивления R контура коэффициент затухания увеличивается, частота колебаний уменьшается, период возрастает и при
При увеличении сопротивления R контура коэффициент затухания увеличивается, частота колебаний уменьшается, период возрастает и при  обращается в бесконечность. Это означает, что процесс перестает быть периодическим,
обращается в бесконечность. Это означает, что процесс перестает быть периодическим, 


