
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
VI.5. Уравнения электромагнитной волныСодержание книги
Поиск на нашем сайте
Основу теории электромагнитного поля составляют уравнения Максвелла (эти уравнения в электродинамике играют такую же роль, что и законы Ньютона в классической механике). Уравнения Максвелла отражают тот факт, что источниками электрического поля могут быть либо электрические заряды, либо изменяющиеся во времени магнитные поля. Магнитные поля могут возбуждаться либо движущимися электрическими зарядами (токами), либо переменными электрическими полями. Таблица 6.1
Уравнения Максвелла приводились в главе 5 учебного пособия. Для удобства дальнейшего изложения запишем эти уравнения еще раз. Полная система уравнений Максвелла в интегральной форме
Эти уравнения связывают значения Полная система уравнений Максвелла в дифференциальной форме
Между величинами, входящими в уравнения Максвелла, существует следующая связь:
Совокупность уравнений (6.29) – (6.35) образует основу электродинамики покоящихся сред. Под ротором вектора
Под дивергенцией вектора
Запишем уравнения Максвелла для однородной нейтральной (
Следовательно, уравнения (6.29) – (6.32) примут вид
Символ rot означает дифференцирование по координатам. Меняя порядок дифференцирования по координатам и времени, можно записать
Произведя в уравнении (6.42) эту замену и подставив в получившееся выражение формулу (6.40), получим
Применив операцию rot к уравнению (6.40) и произведя аналогичные преобразования, получим уравнение
Найдем проекцию векторного уравнения (6.43) на ось х:
По определению ротора (см. формулы (6.36))
Подставляя в это выражение значения
Прибавляя и вычитая

Учитывая (6.41), уравнение (6.45) можно записать следующим образом:
Аналогичные уравнения получаются для
Сходным образом уравнение (6.44) можно преобразовать к виду
Уравнения (6.47) и (6.48) неразрывно связаны друг с другом, так как они получены из уравнений (6.38) и (6.40), каждое из которых содержит и Как отмечалось ранее при рассмотрении механических волн, дифференциальное уравнение вида
представляет собой волновое уравнение. Всякая функция, удовлетворяющая такому уравнению, описывает некоторую волну. Таким образом, уравнения (6.47) и (6.48) указывают на то, что электромагнитные поля могут существовать в виде электромагнитных волн, фазовая скорость которых равна
Для вакуума по формуле (6.49) получается
Таким образом, фазовая скорость электромагнитных волн
и в вакууме совпадает со скоростью света.
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 199; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.116.77 (0.006 с.) |

 -излучение
-излучение
 (6.25)
(6.25)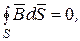 (6.26)
(6.26) (6.27)
(6.27) (6.28)
(6.28)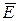 или
или  вдоль некоторого контура со значениями
вдоль некоторого контура со значениями 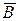 (соответственно
(соответственно  ) в точках опирающейся на контур
) в точках опирающейся на контур  (6.29)
(6.29) (6.30)
(6.30) (6.31)
(6.31) (6.32)
(6.32) (6.33)
(6.33) (6.34)
(6.34) (6.35)
(6.35) (
( ) подразумевается вектор с составляющими:
) подразумевается вектор с составляющими: (6.36)
(6.36) ) подразумевается следующая скалярная величина:
) подразумевается следующая скалярная величина: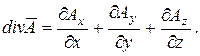 (6.37)
(6.37)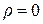 )
)  ) среды с постоянными проницаемостями
) среды с постоянными проницаемостями 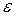 и
и  .
. 



 (6.38)
(6.38) (6.39)
(6.39)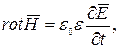 (6.40)
(6.40) (6.41)
(6.41) Применим к уравнению (6.38) операцию rot:
Применим к уравнению (6.38) операцию rot:
 (6.43)
(6.43) (6.44)
(6.44) (6.45)
(6.45)
 и
и  , получим
, получим
 , приведем данное выражение к виду
, приведем данное выражение к виду (6.46)
(6.46) и
и  . Объединив уравнения для всех трех компонент, получим дифференциальное уравнение для вектора
. Объединив уравнения для всех трех компонент, получим дифференциальное уравнение для вектора  (6.47)
(6.47) (6.48)
(6.48)

 (6.49)
(6.49)
 (6.50)
(6.50)


