
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
I.8. Проводники в электростатическом поле. КонденсаторыСодержание книги
Поиск на нашем сайте
Если поместить проводник во внешнее электростатическое поле, то это поле будет действовать на свободные заряды проводника, в результате чего они начнут перемещаться – положительные вдоль поля, отрицательные – против поля (рис. 1.17, а). На одном конце проводника будет накапливаться избыток положительного заряда, на другом конце – избыток отрицательного заряда. Процесс происходит до тех пор, пока не установится равновесное распределение зарядов, при котором электростатическое поле внутри Отсутствие поля внутри проводника (
Таким образом, нейтральный проводник, внесенный в электростати-ческое поле, разрывает часть линий напряженности: они заканчиваются на Рассмотрим уединенный проводник, то есть проводник, который удален от других проводников, тел и зарядов. Его потенциал согласно формуле (1.17) прямо пропорционален заряду проводника. Опыт показывает, что разные проводники, будучи одинаково заряженными, имеют различные
где коэффициент пропорциональности
называют электрической емкостью (емкостью) проводника. Емкость уединенного проводника есть физическая скалярная величина, характеризующая способность проводника накапливать электрические заряды. Так как заряды распределяются на внешней поверхности проводника, емкость проводника зависит от его размеров и формы, но не зависит от Единицей емкости в СИ является фарад (Ф): 1 Ф – это емкость такого уединенного проводника, потенциал которого изменяется на 1 В при сообщении ему заряда 1 Кл. Согласно (1.17) потенциал уединенного шара радиуса R, находящегося
Используя формулу (1.39), можно найти емкость шара:
Отсюда следует, что емкостью в 1 Ф обладал бы уединенный шар, находящийся в вакууме и имеющий радиус
что примерно в 1400 раз больше радиуса Земли (электрическая емкость Земли примерно 0,7 миллифарад). Следовательно, фарад – очень большая величина, поэтому на практике используются дольные единицы фарада: Как следует из рассмотренного примера, для того, чтобы проводник Допустим, что уединенный проводник А имеет форму шара. Так как он уединенный, его заряд
Таким образом, конденсатор работает по принципу: электроемкость неуединенного проводника всегда больше электроемкости того же проводника, когда он уединен. Конденсатор представляет собой систему двух проводников (обкладок), разделенных диэлектриком. На емкость конденсатора не должны оказывать влияние окружающие тела, поэтому проводникам придают такую форму, чтобы поле, создаваемое накапливаемыми зарядами, было сосредоточено Так как поле сосредоточено внутри конденсатора, то линии напряжен-ности поля начинаются на одной обкладке и кончаются на другой. Поэтому свободные заряды, возникающие на разных обкладках, являются равными по модулю разноименными зарядами. Емкостью конденсатора называется физическая величина, равная
Рассчитаем емкость плоского конденсатора, состоящего из двух параллельных металлических пластин площадью S каждая, расположенных на расстоянии d друг от друга и имеющих заряды
Учитывая связь между напряженностью поля и потенциалом (
Заменяя в формуле (1.40)
Приведем без вывода формулы для расчета емкости конденсаторов – емкость цилиндрического конденсатора
где R и r – радиусы коаксиальных цилиндров, L – длина образующей цилиндров; – емкость сферического конденсатора
где R и r – радиусы сфер. Конденсаторы характеризуются пробивным напряжением – такой разностью потенциалов между обкладками, при которой происходит пробой – электрический разряд через слой диэлектрика в конденсаторе. Величина пробивного напряжения зависит от формы обкладок, свойств диэлектрика и его толщины. Для увеличения емкости и варьирования ее возможных значений При параллельном соединении (рис. 1.19, а) разность потенциалов между обкладками всех конденсаторов одинакова и составляет
Общий заряд батареи равен сумме зарядов всех конденсаторов
Полная емкость батареи
то есть при параллельном соединении конденсаторов электрическая
При последовательном соединении (рис. 1.19, б) заряды всех конденсаторов одинаковы и равны заряду
где
С другой стороны, откуда
или
то есть при последовательном соединении конденсаторов суммируются
|
|||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 306; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.55.25 (0.007 с.) |

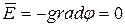 ) означает, что
) означает, что 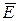 поля направлен по нормали к каждой точке поверхности проводника.
поля направлен по нормали к каждой точке поверхности проводника.
 (1.38)
(1.38) (1.39)
(1.39)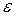 , равен
, равен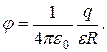
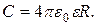

 равномерно распределен по поверхности
равномерно распределен по поверхности  (рис. 1.18, а).
(рис. 1.18, а).  знака (рис. 1.18, б). В свою очередь перераспределяется по поверхности шара А
знака (рис. 1.18, б). В свою очередь перераспределяется по поверхности шара А  . Это соотношение справедливо для всех точек, лежащих на прямой ОМ слева от А. Поскольку
. Это соотношение справедливо для всех точек, лежащих на прямой ОМ слева от А. Поскольку  и
и 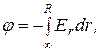 потенциал проводника понижается, что приводит к увеличению его емкости (
потенциал проводника понижается, что приводит к увеличению его емкости ( ).
).
 (1.40)
(1.40) и
и  . Если расстояние между пластинами мало по сравнению с их линейными размерами, то поле между обкладками можно считать однородным и его напряженность
. Если расстояние между пластинами мало по сравнению с их линейными размерами, то поле между обкладками можно считать однородным и его напряженность 
 ), разность потенциалов между пластинами, расстояние между которыми d, равна
), разность потенциалов между пластинами, расстояние между которыми d, равна (1.41)
(1.41) , с учетом (1.41) получим
, с учетом (1.41) получим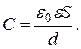 (1.42)
(1.42)
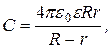
 . Если емкости отдельных конденсаторов
. Если емкости отдельных конденсаторов  то их заряды равны
то их заряды равны
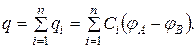
 (1.43)
(1.43)



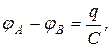

 (1.44)
(1.44) батареи всегда меньше наименьшей емкости конденсатора, используемого в батарее. Преимущество последовательного соединения конденсаторов состоит в том, что на каждый конденсатор приходится лишь часть разности потенциалов между клеммами батареи, что уменьшает вероятность пробоя конденсаторов.
батареи всегда меньше наименьшей емкости конденсатора, используемого в батарее. Преимущество последовательного соединения конденсаторов состоит в том, что на каждый конденсатор приходится лишь часть разности потенциалов между клеммами батареи, что уменьшает вероятность пробоя конденсаторов.


