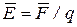Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
I.5. Связь между силовой и энергетической характеристиками электростатического поляСодержание книги
Поиск на нашем сайте
Напряженность и потенциал – различные характеристики одной и той же точки поля. Следовательно, между ними должна существовать однозначная связь. Работа по перемещению положительного единичного точечного заряда из одной точки поля в другую вдоль оси х на элементарное расстояние
где символ частной производной подчеркивает, что дифференцирование производится только по оси х. Повторив аналогичные рассуждения для осей y и z, можем найти вектор
где В математике вектор, показывающий направление наибольшего роста скалярной функции П, называется градиентом (обозначается
то есть напряженность поля равна градиенту потенциала со знаком «минус». Это означает, что вектор напряженности электростатического поля В случае однородного поля (например, поля плоского конденсатора)
где d – расстояние,
Можно доказать, что силовые линии поля всегда нормальны к эквипотенциальным поверхностям. Действительно, все точки эквипотенциальной поверхности имеют одинаковый потенциал, поэтому работа по перемещению заряда вдоль этой поверхности
Эквипотенциальных поверхностей вокруг каждого заряда и системы
|
|||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 1264; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.147.121 (0.008 с.) |

 равна
равна  . С другой стороны, эту работу можно выразить через разность потенциалов на концах отрезка
. С другой стороны, эту работу можно выразить через разность потенциалов на концах отрезка 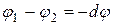 . Приравнивая оба выражения для работы, получим
. Приравнивая оба выражения для работы, получим 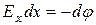 , откуда
, откуда
 (1.20)
(1.20) единичные векторы координатных осей x, y и z (орты).
единичные векторы координатных осей x, y и z (орты). ).
).  (1.21)
(1.21) (1.22)
(1.22) разность потенциалов между обкладками конденсатора. Из формулы (1.22) следует, что напряженность электрического поля можно выражать в вольтах на метр (В/м).
разность потенциалов между обкладками конденсатора. Из формулы (1.22) следует, что напряженность электрического поля можно выражать в вольтах на метр (В/м). Для графического изображения распределения потенциала электростатического поля пользуются эквипотенциальными поверхностями – поверхностями, во всех точках которых потенциал
Для графического изображения распределения потенциала электростатического поля пользуются эквипотенциальными поверхностями – поверхностями, во всех точках которых потенциал  имеет одно и то же значение. Если поле создается точечным зарядом (рис. 1.9), то его потенциал равен
имеет одно и то же значение. Если поле создается точечным зарядом (рис. 1.9), то его потенциал равен  Таким образом,
Таким образом,  Это означает, что электростатические силы, действующие на заряд, всегда направлены по нормали
Это означает, что электростатические силы, действующие на заряд, всегда направлены по нормали