
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
III.2. Закон Био-Савара-ЛапласаСодержание книги
Поиск на нашем сайте
После опытов Эрстеда начались интенсивные исследования магнитного поля постоянного тока. Французские физики Био и Савар в первой четверти XIX в. изучали магнитные поля, создаваемые в воздухе прямолинейным Био и Савар попытались получить закон, который позволял бы рассчитывать индукцию в каждой точке магнитного поля, создаваемого током
где
где Коэффициент пропорциональности где
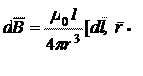 (3.5) (3.5)
Так как модуль векторного произведения
Из выражений (3.4) и (3.5) следует, что магнитная индукция поля, создаваемого в вакууме током I, идущим по проводнику конечной длины и любой формы, равна Закон Био-Савара-Лапласа совместно с принципом суперпозиции позволяет рассчитывать магнитные поля, создаваемые любыми проводниками с током.
В данном случае поле создается Из рис. 3.4 следует: Подставляя эти выражения в формулу (3.6), получим:
Так как угол
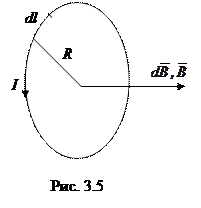
2. Магнитное поле в центре кругового проводника с током. В данном случае все элементы dl кругового проводника с током создают в центре магнитное поле одинакового направления – вдоль нормали от витка (рис. 3.5). Поэтому сложение
Интегрируя это выражение по l, получим
|
||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 229; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.198.250 (0.008 с.) |

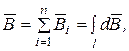 (3.4)
(3.4) индукция магнитного поля малого элемента
индукция магнитного поля малого элемента  проводника с током, а интегрирование проводится по всей длине проводника.
проводника с током, а интегрирование проводится по всей длине проводника. Закон Био-Савара-Лапласа для проводника с током I, элемент которого
Закон Био-Савара-Лапласа для проводника с током I, элемент которого  записывается в виде:
записывается в виде: (3.5)
(3.5) вектор, по модулю равный длине
вектор, по модулю равный длине  радиус-вектор, проведенный от элемента
радиус-вектор, проведенный от элемента  модуль радиуса-вектора. Направление
модуль радиуса-вектора. Направление  и
и  , то есть перпендикулярно плоскости, проведенной через эти векторы, и совпадает
, то есть перпендикулярно плоскости, проведенной через эти векторы, и совпадает  зависит от выбора системы единиц. В СИ это размерная величина, равная
зависит от выбора системы единиц. В СИ это размерная величина, равная 
 магнитная постоянная. Таким образом, в СИ закон Био-Савара-Лапласа имеет вид
магнитная постоянная. Таким образом, в СИ закон Био-Савара-Лапласа имеет вид равен dl r sin α, то модуль вектора
равен dl r sin α, то модуль вектора  определяется выражением
определяется выражением (3.6)
(3.6)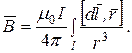 (3.7)
(3.7)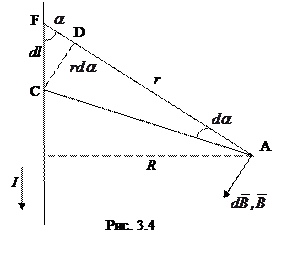 1. Магнитное поле прямого тока.
1. Магнитное поле прямого тока. , выразив через него все остальные величины.
, выразив через него все остальные величины. откуда
откуда  c другой стороны,
c другой стороны,  откуда
откуда 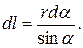
 (3.8)
(3.8) , то согласно (3.7) и (3.8) получим
, то согласно (3.7) и (3.8) получим (3.9)
(3.9)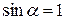 ) и расстояние всех элементов проводника до центра кругового витка одинаково и равно R, то
) и расстояние всех элементов проводника до центра кругового витка одинаково и равно R, то
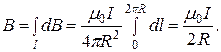 (3.10)
(3.10)


