
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
VI.2. Вынужденные колебания. Переменный электрический токСодержание книги
Поиск на нашем сайте
Для того чтобы в реальной колебательной системе получить незатухающие колебания, необходимо компенсировать в ней потери энергии. Такая компенсация возможна с помощью какого-либо периодически действующего где Если рассматривать процессы в электрическом колебательном контуре, то в качестве
Тогда дифференциальное уравнение вынужденных электромагнитных колебаний в колебательном контуре с учетом (6.8) будет иметь вид
Решением уравнения (6.9) в установившемся режиме является гармоническая функция
где
Установившиеся вынужденные электромагнитные колебания в цепи
или
При частоте Ввиду того, что в течение Действующим (эффективным) значением переменного тока называют такую величину, которая равна силе постоянного тока, выделяющего в проводнике такое же количество теплоты, что и данный переменный ток за
Для мгновенных значений синусоидальных токов выполняются закон Ома и правила Кирхгофа. Рассмотрим цепи, содержащие резистор, катушку индуктивности, конденсатор и все три элемента, соединенные последовательно, на зажимах
где 1. Электрическая цепь с резистором (рис. 6.6). Сила тока, протекающего через резистор, определяется законом Ома
2. Электрическая цепь с катушкой индуктивности (рис. 6.8). В катушке без потерь (
откуда ток
Постоянная интегрирования А =0, так как ток изменяется по гармони-ческому закону, то есть не имеет постоянной составляющей. Очевидно, что амплитуда тока в цепи с катушкой
где
Таким образом, в цепи с катушкой индуктивности колебания силы тока отстают по фазе на  от колебаний напряжения (рис. 6.9). от колебаний напряжения (рис. 6.9).
Сила тока в цепи конденсатора
где
Таким образом, в цепи с конденсатором колебания силы тока опережают по фазе на Рассмотрим теперь электрическую цепь из последовательно соединенных резистора, катушки индуктивности и конденсатора (рис. 6.12).
По второму правилу Кирхгофа для мгновенных значений напряжение на зажимах цепи равно сумме напряжений на отдельных элементах
Построим векторную диаграмму цепи с учетом полученных ранее фазовых соотношений: а) напряжение на резисторе совпадает по фазе с током; Из векторной диаграммы найдем модуль действующего значения
где Учитывая, что
где Z – полное сопротивление цепи. Выражение
называется законом Ома для цепи переменного тока. Разность
Мгновенная мощность, развиваемая
(6.12) Среднее за период значение мгновенной мощности называют активной мощностью тока в электрической цепи:
Из-за наличия сдвига фаз На рис. 6.14 приведены графики При При Подставив (6.12) в (6.13) и выполнив преобразования, найдем среднее значение мощности переменного тока:
где Формула (6.14) показывает, что развиваемая в цепи переменного тока мощность зависит не только от силы тока и напряжения, но и от сдвига фаз между напряжением и током. Коэффициент мощности
|
||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 327; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.131.13.161 (0.01 с.) |

 , изменяющегося, например, по гармоническому закону
, изменяющегося, например, по гармоническому закону  ,
, – циклическая частота внешнего воздействия.
– циклическая частота внешнего воздействия. (6.8)
(6.8) (6.9)
(6.9)




 где
где  – мгновенное значение силы тока, то есть значение тока для каждого момента времени;
– мгновенное значение силы тока, то есть значение тока для каждого момента времени;  – амплитудное значение силы тока.
– амплитудное значение силы тока.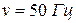 (промышленная частота) период электромагнитных колебаний составляет
(промышленная частота) период электромагнитных колебаний составляет  .
.

 – амплитудное значение напряжения.
– амплитудное значение напряжения.

 – амплитуда силы тока. Очевидно, что при чисто активном (R) характере цепи сдвиг фаз колебаний тока и напряжения равен нулю (рис. 6.7).
– амплитуда силы тока. Очевидно, что при чисто активном (R) характере цепи сдвиг фаз колебаний тока и напряжения равен нулю (рис. 6.7). ) будет протекать ток, если напряжение на ее выводах компенсирует ЭДС самоиндукции, то есть
) будет протекать ток, если напряжение на ее выводах компенсирует ЭДС самоиндукции, то есть


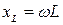 – индуктивное сопротивление, зависящее от частоты. При
– индуктивное сопротивление, зависящее от частоты. При  (при протекании постоянного тока)
(при протекании постоянного тока)  .
.
 3. Электрическая цепь с конденсатором (рис. 6.10). Если пренебречь
3. Электрическая цепь с конденсатором (рис. 6.10). Если пренебречь  будет равно напряжению
будет равно напряжению  откуда заряд конденсатора
откуда заряд конденсатора

 ,
,  – емкостное сопротивление цепи. Чем меньше частота
– емкостное сопротивление цепи. Чем меньше частота  , тем больше
, тем больше  . Поэтому в цепи постоянного тока (
. Поэтому в цепи постоянного тока ( )
)  и конденсатор не проводит электрический ток.
и конденсатор не проводит электрический ток.
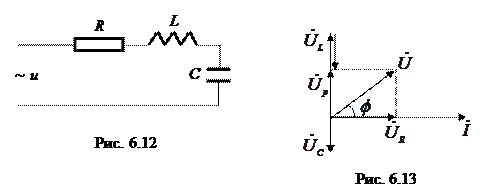



 – реактивная составляющая напряжения.
– реактивная составляющая напряжения. ,
,  ,
,  , получим
, получим
 (6.10)
(6.10) называют реактивным сопротивлением. Из
называют реактивным сопротивлением. Из  (6.11)
(6.11) Если
Если  , цепь имеет индуктивный характер,
, цепь имеет индуктивный характер,  ; если
; если 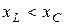 , цепь имеет емкостный характер,
, цепь имеет емкостный характер,  ; если
; если  , то реактивное сопротивление цепи
, то реактивное сопротивление цепи  ,
,  и цепь имеет активный характер даже при
и цепь имеет активный характер даже при 
 (6.13)
(6.13) знаки
знаки  в отдельные промежутки времени мощность отрицательна. Это объясняется тем, что при наличии в цепи катушки индуктивности возрастание тока приводит к созданию в ней магнитного поля, которое обладает
в отдельные промежутки времени мощность отрицательна. Это объясняется тем, что при наличии в цепи катушки индуктивности возрастание тока приводит к созданию в ней магнитного поля, которое обладает  положительная мощность равна отрицательной мощности, работа тока за период равна нулю, следовательно, средняя мощность также равна нулю. При этом периодически энергия запасается в магнитном и электрическом полях, а затем снова передается генератору. Последний случай возможен лишь при R =0.
положительная мощность равна отрицательной мощности, работа тока за период равна нулю, следовательно, средняя мощность также равна нулю. При этом периодически энергия запасается в магнитном и электрическом полях, а затем снова передается генератору. Последний случай возможен лишь при R =0. , (6.14)
, (6.14) – косинус угла сдвига фаз, который называется коэффициентом мощности.
– косинус угла сдвига фаз, который называется коэффициентом мощности. характеризует потери энергии в цепи
характеризует потери энергии в цепи 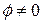 и
и  может быть много меньше единицы. В этих случаях для
может быть много меньше единицы. В этих случаях для  был по возможности ближе к единице.
был по возможности ближе к единице.


