
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
IV.2. Явление самоиндукции. Индуктивность контураСодержание книги
Поиск на нашем сайте
Электрический ток, протекающий в замкнутом контуре, создает вокруг себя магнитное поле, индукция B которого по закону Био-Савара-Лапласа пропорциональна силе тока (B~I). Следовательно, сцепленный с контуром магнитный поток Ф, также пропорционален силе тока (
где L – коэффициент пропорциональности, называемый индуктивностью контура или коэффициентом самоиндукции. При изменении силы тока в контуре будет изменяться и сцепленный Из выражения (4.5) определяется единица индуктивности – генри (Гн): 1 Гн = 1 Вб/А. Индуктивность контура зависит от его геометрической формы, размеров и от магнитных свойств среды, в которой он находится. Например, для
где N – общее число витков соленоида,
Из формул (4.6) и (4.7) следует, что индуктивность катушки, имеющей железный сердечник, больше, чем у катушки без сердечника. Катушка Применяя к явлению самоиндукции закон Фарадея, получим, что ЭДС самоиндукции равна
где знак «минус», обусловленный правилом Ленца, показывает, что наличие индуктивности в контуре приводит к замедлению изменения тока в нем. Из выражения (4.8) следует еще одно определение единицы индуктивности: 1 Гн – это индуктивность такого контура, в котором при изменении тока
1 Гн = 1 (В·с)/А.
IV.3. Взаимная индукция
Если два контура расположены один возле другого и в каждом из них изменяется сила тока, то они будут взаимно влиять друг на друга. Изменение Таким образом, явление взаимоиндукции – это тоже одна из разновидностей электромагнитной индукции. Явление взаимоиндукции характери-зуется коэффициентом взаимоиндукции
где Если ток
Аналогично, при протекании тока силой
Расчеты, подтверждаемые опытом, показывают, что Из формул (4.8) и (4.9) следует, что взаимоиндукция в один генри будет между двумя контурами тогда, когда в одном из них возникает ЭДС Явление взаимоиндукции используется в электротехнических устройствах, которые применяются для повышения и понижения напряжения переменного тока. Такие устройства называют трансформаторами. Индукционные явления служат причиной возникновения внутри металлов паразитных токов. Эти токи называют вихревыми токами или токами Фуко. Природа вихревых токов индуктивная, и возникают они в соответствии Следствием появления вихревых токов является нагревание металла, В металлургии вихревые токи используются для плавки металлов
|
||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 368; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.217.1 (0.006 с.) |

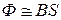 ):
):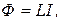 (4.5)
(4.5) ,
,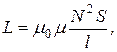 (4.6)
(4.6)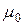 – магнитная постоянная. Учитывая, что объем соленоида
– магнитная постоянная. Учитывая, что объем соленоида 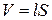 , а
, а 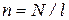 – число витков, приходящихся
– число витков, приходящихся  (4.7)
(4.7)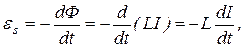 (4.8)
(4.8) и
и  , то есть ток самоиндукции направлен навстречу току внешнего источника и тормозит его возрастание. Если ток в контуре уменьшается, то
, то есть ток самоиндукции направлен навстречу току внешнего источника и тормозит его возрастание. Если ток в контуре уменьшается, то  и
и  , то есть возникающий ток самоиндукции замедляет убывание тока внешнего источника. Таким
, то есть возникающий ток самоиндукции замедляет убывание тока внешнего источника. Таким  В случаях, когда по техническим условиям надо иметь катушку с весьма малой индуктивностью, применяют бифилярные обмотки. Чтобы получить бифилярную обмотку, проволоку складывают вдвое и в таком виде наматывают на каркас катушки (рис. 4.3). При такой намотке ток в каждых двух соседних витках имеет противоположные направления, и поэтому действие
В случаях, когда по техническим условиям надо иметь катушку с весьма малой индуктивностью, применяют бифилярные обмотки. Чтобы получить бифилярную обмотку, проволоку складывают вдвое и в таком виде наматывают на каркас катушки (рис. 4.3). При такой намотке ток в каждых двух соседних витках имеет противоположные направления, и поэтому действие  в первом контуре вызовет появление индуцированной ЭДС во втором контуре и, наоборот, изменение тока
в первом контуре вызовет появление индуцированной ЭДС во втором контуре и, наоборот, изменение тока 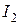 и магнитного поля второго контура будет причиной появления индуцированной ЭДС в первом контуре. Это
и магнитного поля второго контура будет причиной появления индуцированной ЭДС в первом контуре. Это  или
или 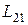 . Его называют также
. Его называют также 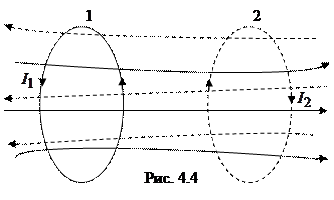 Рассмотрим два неподвижных контура, расположенных достаточно близко друг от друга (рис. 4.4). Если в контуре 1 течет ток
Рассмотрим два неподвижных контура, расположенных достаточно близко друг от друга (рис. 4.4). Если в контуре 1 течет ток 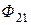 , пронизывающего контур 2, равна
, пронизывающего контур 2, равна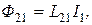
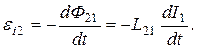 (4.8)
(4.8)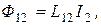
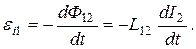 (4.9)
(4.9)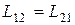 . Эти коэффициенты зависят от геометрической формы, размеров, взаимного расположения контуров и магнитной проницаемости среды, окружающей контуры.
. Эти коэффициенты зависят от геометрической формы, размеров, взаимного расположения контуров и магнитной проницаемости среды, окружающей контуры.


