
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
I.6. Теорема Гаусса для электростатического поля в вакуумеСодержание книги
Поиск на нашем сайте
Вычисление напряженности поля большой системы электрических зарядов с помощью принципа суперпозиции электростатических полей можно Для произвольной замкнутой поверхности S поток вектора напряжен-ности
Этот результат справедлив для замкнутой Рассмотрим теперь общий случай произвольной замкнутой поверхности, окружающей n зарядов. В соответствии с принципом суперпозиции напряженность
Согласно (1.24), каждый из интегралов, стоящий под знаком суммы,
то есть поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на электрическую постоянную. Применим теорему Гаусса для определения напряженности поля равномерно заряженной бесконечной плоскости. В этом случае ее поверхностная плотность заряда
С другой стороны, так как линии
Тогда
Приведем (без вывода) выражения для расчета напряженности электростатического поля, образованного некоторыми другими заряженными телами: 1. Напряженность поля, создаваемого разноименно заряженными параллельными бесконечно протяженными плоскостями (поле плоского конденсатора)
2. Напряженность поля, образованного заряженным шаром
где 3. Напряженность поля равномерно заряженной бесконечно длинной
где
|
|||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 316; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.190.25.139 (0.009 с.) |

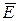 через эту поверхность определяется выражением
через эту поверхность определяется выражением (1.23)
(1.23) где
где  проекция вектора
проекция вектора 
 вектор, модуль которого равен dS, а направление совпадает
вектор, модуль которого равен dS, а направление совпадает  ).
). Рассмотрим сферическую поверхность радиуса r, охватывающую точечный заряд q, находящийся в ее центре (рис. 1.11). В соответствии с формулой (1.23) поток вектора напряженности сквозь эту поверхность равен
Рассмотрим сферическую поверхность радиуса r, охватывающую точечный заряд q, находящийся в ее центре (рис. 1.11). В соответствии с формулой (1.23) поток вектора напряженности сквозь эту поверхность равен (1.24)
(1.24) полей, обусловленных каждым зарядом в отдельности; поэтому поток вектора
полей, обусловленных каждым зарядом в отдельности; поэтому поток вектора 
 . Следовательно,
. Следовательно, (1.25)
(1.25) одинакова в любом месте плоскости. Это означает, что линии напряженности перпендикулярны плоскости в любой точке,
одинакова в любом месте плоскости. Это означает, что линии напряженности перпендикулярны плоскости в любой точке,  Мысленно выделим в пространстве цилиндр, ось которого перпендикулярна плоскости и одно из оснований проходит через интересующую нас точку. Согласно теореме Гаусса,
Мысленно выделим в пространстве цилиндр, ось которого перпендикулярна плоскости и одно из оснований проходит через интересующую нас точку. Согласно теореме Гаусса,

 откуда
откуда (1.26)
(1.26) (1.27)
(1.27) (1.28)
(1.28) заряд шара радиуса
заряд шара радиуса  ;
; 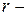 расстояние от центра шара до точки поля (
расстояние от центра шара до точки поля ( ).
). (1.29)
(1.29) линейная плотность заряда на нити (заряд, приходящийся
линейная плотность заряда на нити (заряд, приходящийся 


