
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
I.3. Электростатическое поле. Напряженность поляСодержание книги
Поиск на нашем сайте
Если в пространство, окружающее электрический заряд, внести другой заряд, то между ними возникнет кулоновское взаимодействие. Следовательно, в пространстве, окружающем электрические заряды, существует силовое поле, в данном случае электрическое поле, являющееся средой взаимо-действия между зарядами. Так как рассматриваются неподвижные заряды, Для обнаружения и исследования электростатического поля используется пробный заряд – такой точечный положительный заряд, который не искажает исследуемое поле, то есть не вызывает в нем перераспределения Если в поле, создаваемое зарядом
Как следует из формул (1.5) и (1.2),

или в скалярной форме
Направление вектора
Графически электростатическое поле изображают с помощью линий напряженности – линий, касательные к которым в каждой точке
Электрическое поле называется однородным, если во всех его точках напряженность поля одинакова по модулю и направлению (  ). ). Примером такого поля может быть электростатическое поле плоского конденсатора вдали от краев его обкладок. Рассмотрим метод определения значения и направления вектора напряженности Опытным путем доказано, что к кулоновским силам применим принцип независимости действия сил, рассмотренный в механике, то есть результирующая сила
Согласно (1.5)
или
Формула (1.8) выражает принцип суперпозиции (наложения) электростатических полей, согласно которому напряженность результирующего поля, создаваемого в данной точке пространства системой зарядов или заряженных тел, равна геометрической сумме напряженностей полей, создаваемых Применим принцип суперпозиции для расчета электростатического поля электрического диполя. Электрический диполь – это система двух равных по модулю разноименных точечных зарядов, расстояние между которыми значительно меньше расстояний до рассматриваемых точек поля.
совпадающий по направлению с плечом Согласно принципу суперпозиции (1.8), напряженность поля диполя
где 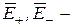 напряженности полей, создаваемых соответственно положительным и отрицательным зарядами диполя. В качестве примера рассчитаем напряженность поля на продолжении оси диполя (в точке А на рис. 1.7). напряженности полей, создаваемых соответственно положительным и отрицательным зарядами диполя. В качестве примера рассчитаем напряженность поля на продолжении оси диполя (в точке А на рис. 1.7).
В данном случае вектор напряженности результирующего поля в точке Анаправлен по оси диполя и по модулю равен
Обозначив расстояние от точки А до середины оси диполя через r, на основании формулы (1.6) для вакуума можно записать
Согласно определению диполя,
|
||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 262; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.17.175 (0.006 с.) |

 , в разных точках помещать пробный заряд
, в разных точках помещать пробный заряд  , то на него будет действовать сила
, то на него будет действовать сила  , различная в этих точках поля и согласно (1.3) пропорциональная величине пробного заряда (рис. 1.2). Однако отношение
, различная в этих точках поля и согласно (1.3) пропорциональная величине пробного заряда (рис. 1.2). Однако отношение  не зависит от
не зависит от  Таким образом, напряженность электростатического поля в данной точке есть векторная физическая величина, определяемая силой, действующей со стороны поля на неподвижный единичный пробный заряд, помещенный в эту точку поля:
Таким образом, напряженность электростатического поля в данной точке есть векторная физическая величина, определяемая силой, действующей со стороны поля на неподвижный единичный пробный заряд, помещенный в эту точку поля: (1.5)
(1.5)
 (1.6)
(1.6)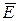 совпадает с направлением силы, действующей на положительный заряд. Если поле создается положительным зарядом (рис. 1.3), то вектор
совпадает с направлением силы, действующей на положительный заряд. Если поле создается положительным зарядом (рис. 1.3), то вектор  Из формулы (1.5) следует, что единица напряженности электростатического поля – ньютон на кулон (Н/Кл): 1 Н/Кл – напряженность
Из формулы (1.5) следует, что единица напряженности электростатического поля – ньютон на кулон (Н/Кл): 1 Н/Кл – напряженность 
 находящейся в вакууме.
находящейся в вакууме. , равна векторной сумме сил
, равна векторной сумме сил  , приложенных к нему со стороны каждого из
, приложенных к нему со стороны каждого из  системы:
системы: (1.7)
(1.7) и
и  , где
, где  напряженность результирующего поля,
напряженность результирующего поля,  напряженность поля, создаваемого зарядом
напряженность поля, создаваемого зарядом 
 (1.8)
(1.8) Вектор, направленный по оси диполя (прямой, проходящей через оба заряда) от отрицательного заряда к положительному и равный расстоянию между ними,
Вектор, направленный по оси диполя (прямой, проходящей через оба заряда) от отрицательного заряда к положительному и равный расстоянию между ними,  (рис. 1.6).
(рис. 1.6).  (1.9)
(1.9)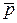 или дипольным моментом.
или дипольным моментом.



 , поэтому
, поэтому



