
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
V.1. Вихревое электрическое полеСодержание книги
Поиск на нашем сайте
В 60-х гг. XIX в. английский ученый Дж. Максвелл (1831-1879) обобщил экспериментально установленные законы электрического и магнитного Согласно закону электромагнитной индукции Фарадея, всякое изменение магнитного поля во времени Однако ЭДС в любой цепи обусловлена действием на носители тока сторонних сил неэлектростатического происхождения. Поэтому, прежде всего, возникает вопрос о природе сторонних сил в данном случае. Опыт показывает, что в случае электромагнитной индукции сторонние силы не связаны ни с тепловыми, ни с химическими процессами в контуре. Их возникновение также нельзя объяснить силой Лоренца, так как она Максвелл выдвинул гипотезу, что всякое переменное магнитное поле возбуждает в окружающем пространстве вихревое электрическое поле
Уравнение (5.1) называют вторым уравнением Максвелла. Смысл этого уравнения заключается в том, что изменяющееся магнитное поле порождает вихревое электрическое, а последнее в свою очередь вызывает в окружающем диэлектрике или вакууме изменяющееся магнитное поле. Поскольку магнитное поле создается электрическим током, то, согласно Максвеллу, вихревое электрическое поле следует рассматривать как некоторый ток, Подставив в (5.1) выражение для потока магнитной индукции
Если поверхность и контур неподвижны, то операции дифференцирования и интегрирования можно поменять местами. Следовательно,
где символ частной производной подчеркивает тот факт, что интеграл Как рассматривалось ранее (см. 1.4), циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю,
Сравнивая это выражение с (5.1), видим, что между полями
V.2. Ток смещения
Механизм возникновения тока смещения в диэлектрике можно понять, рассмотрев один из опытов Токи смещения наблюдаются в конденсаторе, включенном в цепь переменного тока. Для цепи постоянного тока конденсатор является бесконечно большим сопротивлением, если только его диэлектрик не обладает утечкой. В такой цепи лишь в момент ее замыкания протекает импульс зарядного тока, соответствующий максимальному смещению электронов проводимости. Если цепь с конденсатором питать переменным током, то в ней за каждый период протекают токи заряда и разряда конденсатора, сопротивление которого теперь не бесконечно большое, а зависит от емкости конденсатора и частоты тока Согласно воззрениям Фарадея и Максвелла, конденсатор нужно рассматривать не как разрыв цепи, а как участок с другим механизмом проводимости. Если между обкладками конденсатора находится полярный или поляризующийся в электрическом поле диэлектрик, то при наличии разности потенциалов между обкладками конденсатора электрические заряды смещаются вдоль линий напряженности поля. Это смещение ионов образует ток смещения в диэлектрике. Ток смещения существует не только в диэлектрике, но и в вакууме,
где
С другой стороны силу тока сквозь произвольную поверхность S можно определить как поток вектора плотности тока
Тогда
Сравнивая это выражение с (5.3), получим
В свою очередь электрическое смещение
где Таким образом, ток смещения, как это следует из теории Максвелла В своей теории Максвелл ввел понятие полного тока, равного сумме
По Максвеллу полный ток в цепи всегда замкнут, то есть на концах проводников обрывается лишь ток проводимости, а в диэлектрике (вакууме) между концами проводника имеется ток смещения, который замыкает ток проводимости. Введя понятие полного тока, Максвелл обобщил теорему о циркуляции вектора
Уравнение (5.6) называется первым уравнением Максвелла в интегральной форме. Оно представляет собой обобщенный закон полного тока и выражает основное положение электромагнитной теории: токи смещения создают такие же магнитные поля, как и токи проводимости.
|
||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 335; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.205.110 (0.006 с.) |

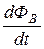 приводит к возникновению ЭДС
приводит к возникновению ЭДС 
 , циркуляция которого и является причиной возникновения ЭДС электромагнитной индукции в контуре:
, циркуляция которого и является причиной возникновения ЭДС электромагнитной индукции в контуре: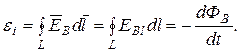 (5.1)
(5.1)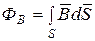 , получим
, получим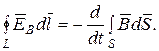
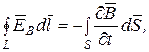 (5.2)
(5.2)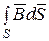 является функцией только от времени.
является функцией только от времени.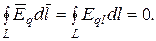
 имеется принципиальное различие: циркуляция вектора
имеется принципиальное различие: циркуляция вектора 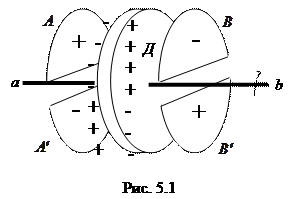 Ток смещения введен Максвеллом для установления количественных соотношений между переменным электрическим полем и вызываемым им вихревым магнитным полем.
Ток смещения введен Максвеллом для установления количественных соотношений между переменным электрическим полем и вызываемым им вихревым магнитным полем.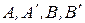 . При прохождении точками диска плоскости ab, разделяющей заряженные
. При прохождении точками диска плоскости ab, разделяющей заряженные 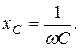
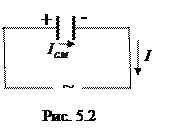 Рассмотрим процессы, протекающие в цепи переменного тока, содержащей конденсатор (рис. 5.2).
Рассмотрим процессы, протекающие в цепи переменного тока, содержащей конденсатор (рис. 5.2). 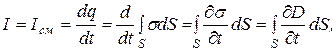
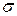 – поверхностная плотность заряда на обкладках конденсатора; D – электрическое смещение в конденсаторе, причем
– поверхностная плотность заряда на обкладках конденсатора; D – электрическое смещение в конденсаторе, причем 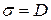 . Подынтегральное выражение можно рассматривать как частный случай
. Подынтегральное выражение можно рассматривать как частный случай 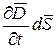 , когда
, когда 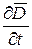 и
и 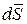 взаимно параллельны. Поэтому для общего случая
взаимно параллельны. Поэтому для общего случая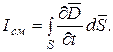 (5.3)
(5.3)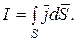
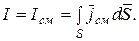
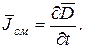 (5.4)
(5.4)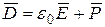 , где
, где 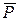 – вектор поляризации. Следовательно, плотность тока смещения
– вектор поляризации. Следовательно, плотность тока смещения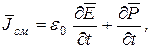 (5.5)
(5.5)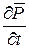 – плотность тока поляризации, обусловленного движением электрических зарядов в диэлектрике. Этот ток возбуждает свою составляющую магнитного поля, так как токи поляризации по своей природе не отличаются от токов проводимости;
– плотность тока поляризации, обусловленного движением электрических зарядов в диэлектрике. Этот ток возбуждает свою составляющую магнитного поля, так как токи поляризации по своей природе не отличаются от токов проводимости; 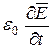 – плотность тока смещения в вакууме,
– плотность тока смещения в вакууме, 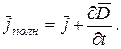
 (или
(или 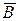 ):
): (5.6)
(5.6)


