Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Основные физические величины и их единицы в СИ
| Физическая
величина
| Наименование
единицы
| Обозначение
| Определение
| | Длина
| Метр
| м
| Метр равен расстоянию, проходимому в вакууме плоской электромагнитной волной за 1/299 792 456 долей секунды.
| | Масса
| Килограмм
| кг
| Килограмм равен массе международного прототипа килограмма.
| | Время
| Секунда
| с
| Секунда равна 9 192 631 770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133.
| | Сила тока
| Ампер
| А
| Ампер равен силе постоянного тока, который при прохождении по двум прямолинейным параллельным проводникам бесконечной длины и ничтожно малой площади поперечного сечения, расположенным в вакууме на расстоянии 1 м один от другого, вызывает между ними силу взаимодействия, равную 2∙10-7 Н на каждый метр длины проводников.
| | Термодинамическая температура
|
Кельвин
|
К
| Кельвин равен 1/273,16 части термодинамической температуры тройной точки воды.
| | Количество вещества
| Моль
| моль
| Моль равен количеству вещества, содержащего столько же структурных элементов, сколько содержится атомов в углероде-12 массой 0,012 кг.
| | Сила света
| Кандела
| кд
| Кандела равна силе света в заданном направлении источника, испускающего монохроматическое излучение частотой 540∙1012 Гц, энергетическая сила света которого в этом направлении составляет 1/683 Вт/ср.
|
Приложение 2
Производные единицы электрических и магнитных величин
| Физическая
величина
| Наименование
единицы
| Обозначение
| Определение
| | Количество электричества, электрический заряд
|
Кулон
|
Кл
| Кулон равен количеству электричества, проходящего через поперечное сечение при токе силой 1 А за время 1 с.
| | Напряженность электрического поля
|
Вольт на метр
|
В/м
| Вольт на метр равен напряженности однородного электрического поля, при которой между двумя точками, находящимися на линии напряженности поля на расстоянии 1 м, создается разность потенциалов 1 В.
| | Электрическое напряжение, электрический потенциал, разность электрических потенциалов, электродвижущая сила
|
Вольт
|
В
| Вольт равен электрическому напряжению на участке электрической цепи, при котором в участке проходит постоянный ток силой 1 А и затрачивается мощность 1 Вт.
| | Электрическая емкость
| Фарад
| Ф
| Фарад равен электрической емкости конденсатора, при которой заряд 1 Кл создает на конденсаторе напряжение 1 В.
| | Магнитная индукция
| Тесла
| Тл
| Тесла равен магнитной индукции, при которой магнитный поток сквозь поперечное сечение площадью 1 м2 равен 1 Вб.
| | Магнитный поток
| Вебер
| Вб
| Вебер равен магнитному потоку, при убывании которого до нуля в сцепленной с ним электрической цепи сопротивлением 1 Ом через поперечное сечение проводника проходит количество электричества 1 Кл.
| | Индуктивность
| Генри
| Гн
| Генри равен индуктивности электрической цепи, с которой при силе постоянного тока в ней 1 А сцепляется магнитный поток 1 Вб.
| | Электрическое сопротивление
| Ом
| Ом
| Ом равен электрическому сопротивлению участка электрической цепи, при котором постоянный ток силой 1 А вызывает падение напряжения 1 В.
|
Приложение 3
Элементы векторной алгебры
Векторное поле
Если каждой точке М ставится в соответствие вектор  , то говорят о векторном , то говорят о векторном
поле  (например, поле электрической напряженности, гравитационное поле, поле магнитной напряженности). В декартовых координатах (например, поле электрической напряженности, гравитационное поле, поле магнитной напряженности). В декартовых координатах

где  – радиус-вектор. Компоненты A x, A y, A z образуют три скалярных поля и однозначно определяют – радиус-вектор. Компоненты A x, A y, A z образуют три скалярных поля и однозначно определяют  – векторную функцию векторного аргумента. – векторную функцию векторного аргумента.
Дивергенция векторного поля
Дивергенцией векторного поля  (обозначается (обозначается  ) называют ) называют
следующую производную по объему поля в точке М:

Величина  есть скалярный поток векторного поля через замкнутую поверхность S, которая окружает точку М и охватывает область G с объемом V. есть скалярный поток векторного поля через замкнутую поверхность S, которая окружает точку М и охватывает область G с объемом V.
Дивергенция 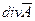 есть мера источников поля есть мера источников поля  . Если в области G . Если в области G  , то векторное поле , то векторное поле  называется свободным от источников. Те точки поля, в которых называется свободным от источников. Те точки поля, в которых  , принято называть источниками поля, а те, в которых , принято называть источниками поля, а те, в которых  – стоками поля. – стоками поля.
Ротор векторного поля
Ротором (вихрем) векторного поля  (обозначается (обозначается  ) называют следующую производную по объему поля в точке М: ) называют следующую производную по объему поля в точке М:

Теорема Стокса
Циркуляция векторного поля  по замкнутой кривой L равна потоку ротора этого поля через поверхность S, опирающуюся на кривую L: по замкнутой кривой L равна потоку ротора этого поля через поверхность S, опирающуюся на кривую L:
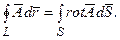
|



 , то говорят о векторном
, то говорят о векторном  (например, поле электрической напряженности, гравитационное поле, поле магнитной напряженности). В декартовых координатах
(например, поле электрической напряженности, гравитационное поле, поле магнитной напряженности). В декартовых координатах
 – радиус-вектор. Компоненты A x, A y, A z образуют три скалярных поля и однозначно определяют
– радиус-вектор. Компоненты A x, A y, A z образуют три скалярных поля и однозначно определяют  – векторную функцию векторного аргумента.
– векторную функцию векторного аргумента. ) называют
) называют 
 есть скалярный поток векторного поля через замкнутую поверхность S, которая окружает точку М и охватывает область G с объемом V.
есть скалярный поток векторного поля через замкнутую поверхность S, которая окружает точку М и охватывает область G с объемом V.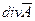 есть мера источников поля
есть мера источников поля  , то векторное поле
, то векторное поле  , принято называть источниками поля, а те, в которых
, принято называть источниками поля, а те, в которых  – стоками поля.
– стоками поля. ) называют следующую производную по объему поля в точке М:
) называют следующую производную по объему поля в точке М: