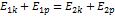Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Колебательное движение. Гармонические колебания и их характеристики.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Колебаниями называются движения или процессы, характеризующиеся определенной повторяемостью во времени. Колебательные процессы имеют широкое распространение в природе и технике, например качание маятника часов, переменный электрический ток и т. д. При колебательном движении маятника меняет свое положение координата его центра масс, при переменном токе меняют свои характеристики с определенной повторяемостью напряжение и ток в цепи. Колебательный процесс может имет различную физическую природу, поэтому различают колебания механические, электромагнитные и др. Но различные колебательные процессы характеризуются одинаковыми физическими параметрами и одинаковыми уравнениями. Колебания называются свободными, если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на систему, которая совершает колебания. Простейшим типом колебаний являются гармонические колебания — колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (косинуса). Исследование гармонических колебаний важно по двум причинам: 1) колебания, которые встречаются в природе и технике, часто имеют близкий к гармоническому характер; 2) различные периодические процессы (процессы, которые повторяются через равные промежутки времени) можно представить как суперпозицию (наложение) гармонических колебаний. Гармонические колебания некоторой величины s описываются уравнением вида
где ω0 — круговая (циклическая) частота, А - максимальное значение колеблющейся величины, называемое амплитудой колебания, φ — начальная фаза колебания в момент времени t=0, (ω0t+φ) - фаза колебания в момент времени t. Фаза колебания есть значение колеблющейся величины в данный момент времени. Так как косинус имеет значение в пределах от +1 до –1, то s может принимать значения от +А до –А. Определенные состояния системы, которая совершает гармонические колебания, повторяются через промежуток времени Т, имеющий название период колебания, за который фаза колебания получает приращение (изменение) 2π, т. е. Гармоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса. Например, гармонически колеблется величина, изменяющаяся во времени следующим образом:
где х — значение изменяющейся величины, t — время, остальные параметры — постоянные: А — амплитуда колебаний, ω — циклическая частота колебаний,
Пружинный и математический маятники. Энергетические превращения при их колебаниях. Существуюет системы, представляющие собой тело определенной массы, подвешенное на нити или стержне (например, качели, маятник часов, отвес). Моделью этих систем является математический маятник. Математический маятник представляет собой тело, подвешенное на нити, размеры которого много меньше длины нити.Считается, что нить нерастяжима и не имеет массы, вся масса такого маятника сосредоточена в подвешенном к нити тела. При этом тело можно считать материальной точкой. Математический маятник совершает колебания под действием внутренних сил: силы тяжести и силы упругости. Колебания, происходящие под действием внутренних сил, называют свободными. Запишем уравнение колебаний математического маятника:
Пружинный маятник — это груз, прикрепленный к пружине. В этой модели маятника мы пренебрегаем массой пружины по сравнению с массой груза, деформацией тела по сравнению с деформацией пружины. Пружинный маятник будет совершать свободные колебания относительно положения равновесия под действием переменной силы. Соответственно в процессе движения изменяются и скорость, и ускорение аналогично тому, как это происходит с математическим маятником. Получим уравнение колебаний для пружинного маятника:
Энергетическое превращение:
Закон сохранения:
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1330; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.124.80 (0.006 с.) |


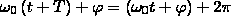 , откуда
, откуда  .
.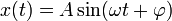 Или
Или 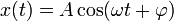 ,
,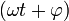 — полная фаза колебаний,
— полная фаза колебаний, 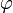 — начальная фаза колебаний.
— начальная фаза колебаний.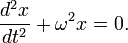 -Обобщенное гармоническое колебание в дифференциальном виде
-Обобщенное гармоническое колебание в дифференциальном виде
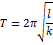
 ,
,  ,
,