
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторные работы :15, 17-КолебанияСодержание книги
Поиск на нашем сайте План упражнений на второй семестр Лабораторные работы:15, 17-Колебания Оптика Полупроводники
Упр. 1. Гармонические колебания (механические и электромагнитные). Затухающие Колебания. Сложение колебаний. Векторные диаграммы. Вынужденные колебания. Диктант «Характеристики затухающих колебаний» 6-7 вопросов В классе 6. 10, 6.19, 40, 53, 57, 60, Дома 6.11,12, 35, 37, 54, 21, 24(8), 29(1), 69, Для самостоятельного решения:
2. Написать уравнение движения при сложении двух одинаково направленных гармонических колебаний, с одинаковым периодом T = 8 с и одинаковой амплитудой A = 0,02 м. Разность фаз колебаний f2 - f1 = p/4. Начальная фаза одного из колебаний равна нулю. Какова будет амплитуда результирующего колебания, если колебания будут во взаимно-перпендикулярных плоскостях? 3. Точка участвует в двух взаимно перпендикулярных колебаниях x = sin(pt) см и y = 2sin(pt + p/2) см. Найти траекторию результирующего движения точки, начертить ее. 4. Уравнение изменения со временем тока в колебательном контуре имеет вид I = -0,02sin(400pt) А, индуктивность контура L = 1 Гн. Найти период колебаний, емкость контура, и максимальные энергии магнитного и электрического полей 5. К невесомой пружине подвесили грузик, и она растянулась на Δх = 9.8 см. С каким периодом будет колебаться грузик, если ему дать толчок в вертикальном направлении? Логарифмический декремент затухания λ=3.1. 6. Найти добротность математического маятника длины l = 50 см, если за промежуток времени τ=5.2 мин его полная энергия уменьшилась в η= 40000 раз. 7. Математический маятник совершает колебания в среде, для которой логарифмический декремент затухания λ=1.5. Каким будет значение λ1, если сопротивление среды увеличить в n=2 раза? 8. Найти добротность осциллятора, у которого амплитуда смещения уменьшается в η=2 раза через каждые n=110 периодов колебаний. 9. Амплитуда затухающих колебаний математического маятника уменьшилась за время t1 = 1 мин в вдвое. Во сколько раз уменьшится амплитуда за t2 = 3 мин? Найти декремент затухания b. 10. Колебательный контур состоит из конденсатора с емкостью 0,2 мкФ и катушки с индуктивностью 5,07 мГн. При каком логарифмическом декременте затухания λ разность потенциалов на обкладках конденсатора за время t = 1 мс уменьшилось в три раза? Каково сопротивление контура R?
13. Из с/р № 1-40 ЧЕТНЫЕ Упр. 2. Механические и электромагнитные волны Диктант по определениям «Волны и их характеристики» 5-6 вопросов. В классе: 1. Уравнение незатухающих колебаний дано в виде х=4 cos(pt) см. Найти смещение от положения равновесия точки, находящейся на расстоянии 75 см от источника колебаний, через 0.01 с после начала колебаний. Скорость распространения колебаний 300 м/с.
2. Источник создает колебания по закону y=sin(2.5πt), см. Скорость распространения волны 100 м/с. Определить смещение, скорость и ускорение колебаний точки, находящейся на расстоянии 20 м от источника в момент t=1 с.
3. Чему равна разность фаз колебаний Dj частиц среды, отстоящих от источника колебаний на расстояниях х1=2 м и х2 = 4 м. Длина волны 1 м
4. В упругой среде распространяется монохроматическая волна ς=А cos(ωt-π/2), где А=0.2 м. В начальный момент времени t=0 все частицы среды находились в покое. На графике дана зависимость смещения частицы, отстоящей от источника колебаний на расстоянии х= 1 м, разность фаз между точкой и источником колебаний составляет 5π/2. Найти период, длину волны, фазовую скорость волны, а также амплитуду колебаний скорости и ускорения частиц среды.
5. Дана электромагнитная волна, у которой амплитуда колебаний индукции магнитного поля Вm=2 мкТл, длина волны 4 м, магнитная проницаемость среды μ=1, ε=9. Найти период колебаний, амплитудное значение Еm, вектор Пойнтинга, интенсивность волны, объемную плотность энергии электрического поля, концентрацию фотонов. Нарисовать график «фотографии волны». 6. Рассчитать максимальное напряжение, которое появляется в антенне метровой длины, находящейся на расстоянии R=100 км от радиостанции, излучающей мощность <P>=100 кВт. Считать диаграмму направленности излучения радиостанции сферической. 7. Уравнение плоской звуковой волны имеет вид ζ= 60 cos(1800t - 5.3x), где ζ – в мкм, х - в метрах. Найти отношение амплитуды смещения частиц среды к длине волны, а также амплитуду колебаний скорости частиц среды и ее отношение к скорости распространения волны. 8. Из с/р № 43-49 Дома: 7. 3,6,10, 20, 21,22 Упр. 3. Интерференция. Вопросы к диктанту: интерференция, когерентные волны, геометрический путь, оптический путь, оптическая разность хода, условия макс/мин интерференции, показать интерферирующие лучи в: тонкая пленка равной толщины/кольца Ньютона. В классе 30. 4, 14, 18, 28, 30,37 Дома 30. 10, 16, 19, 20, 24, 27, 29, 38 – везде построить ход лучей!!! Из с/р № 1-15 «Волновая оптика» Из с/р № 16-38 «Волновая оптика» Упр.5. ТК «Колебания. Волны. Волновая оптика». При успешной сдаче материал снимается с экзамена.
Упр.6. Тепловое излучение. Диктант - энергетическая светимость, спектральная плотность энергетической светимости, спектральный коэффициент поглощения, абсолютно черное тело (а.ч.т.), серое тело. Закон Кирхгофа. Законы излучения а.ч.т.– спектральная плотность энергетической светимости, закон Стефана – Больцмана, закон смещения Вина, второй закон Вина. Формула Релея – Джинса, «ультрафиолетовая катастрофа», формула Планка. В классе: 34. 3, 8, 11, 18, 21 1) АЧТ имеет температуру Т1 = 500 К, Какова будет температура Т2 тела, если энергетическая светимость увеличится в 5 раз. 2) Как и во сколько раз изменится энергетическая светимость АЧТ, если максимум энергии излучения сместится с λ1=780 нм на λ2=390 нм? 3) 3) Длина волны, на которую приходиться максимум энергии в спектре АЧТ λм=0.58 мкм. Определить энергетическую светимость. Дома 34. 6, 10, 16, 19, 22 В классе 35. 4, 7, 36.4, 10, 37. 4, 9 39.2, 9 1) Фотон рентгеновского излучения Е=0.2 МэВ испытывает рассеяние на покоившемся свободном электроне, в результате чего его длина волны увеличилась на Δλ= 2 пм. Найти угол φ, под которым вылетит электрон отдачи. 2) При некотором Uз фототок с поверхности лития, освещаемого электромагнитным излучением с λ0, прекращается. Изменив длину волны в η=1.5 раза, установили, что для прекращения фототока необходимо увеличить Uз в n = 2 раза. Работа выхода электронов с поверхности лития равна А=2.39 эВ. Найти λ0 Дома: 35. 5, 8, 9 36.7, 12 37. 5, 8, 10 39. 4, 5 Дома: 45. 8, 9. 12, 13 Из с/р «Длина волны де Бройля, соотношения неопределенностей, потенциальная яма» № 1-14. Из с/р «Ядро» Колебания и волны. N1. Уравнение колебаний материальной точки массой m=10г имеет вид N2. Написать уравнение гармонического колебания, если максимальное ускорение точки аm=49,3см/c2, период колебаний Т=2с, смещение точки от положения равновесия в начальный момент времени х0=25 мм. N3. Начальная фаза гармонического колебания равна нулю. При смещении точки от положения равновесия х1=2,4 см скорость точки v1=3см/c, а при смещении х2=2,8 см скорость точки v2=2см/c. Найти амплитуду и период этого колебания. N4. Точка совершает гармоническое колебание по закону N5. Написать уравнение гармонического колебания с амплитудой А = 5 см, если за время t = 1 мин совершается 150 колебаний и начальная фаза колебаний равна π/4. Начертить график этого движения. N6. Через какое время от начала движения точка, совершающая гармоническое колебание по закону косинуса, сместится от положения равновесия на половину амплитуды? Период колебаний Т = 24 с, начальная фаза равна нулю. N7. Уравнение движения точки дано в виде
N8. Уравнение движения точки дано в виде N9. Найти отношение кинетической энергии точки к ее потенциальной энергии для моментов времени а) t = T/12, б) t = T/8 N10. Найти отношение кинетической энергии точки к ее потенциальной энергии для моментов, когда смещение точки от положения равновесия составляет а) х = А/4, б) х = А/2. N11. Полная энергия тела, совершающего гармоническое колебание, W = 30 мкДж; максимальная сила, действующая на тело Fmax = 1,5 мН. Написать уравнение движения этого тела, если период колебаний Т = 2 с, начальная фаза φ = π/3. N12. Амплитуда гармонических колебаний материальной точки А = 2 см, полная энергия колебаний W = 0,3 мкДж. При каком смещении х от положения равновесия на колеблющуюся точку действует сила F = 22,5 мкН. N13. Уравнение изменения со временем разности потенциалов на обкладках конденсатора в колебательном контуре имеет вид U=50Cos104pt, В. Емкость конденсатора С=0,1 мкФ. Найти период колебаний, индуктивность контура, закон изменения со временем тока и длину волны, соответствующую этому контуру. N14. В идеальном колебательном контуре заряд конденсатора изменяется по закону q = 4×10-3cos104 t Кл. Если индуктивность контура L = 2 мГн, а Т - период колебаний, то в момент времени t = Т /8 энергия W э электрического поля конденсатора равна … N15. Максимальное напряжение на обкладках конденсатора в идеальном колебательном контуре Um =300 В. Если индуктивность контура L = 10-2 Гн, период колебания Т = 2p×10-3 с, то максимальная энергия электрического поля W э max конденсатора равна... N16. В идеальном колебательном контуре происходят свободные гармонические колебания. В момент времени t = T /8, где Т – период колебаний, отношение энергии N17. В колебательном контуре с индуктивностью L = 10-3 Гн происходят свободные гармонические колебания. Если максимальное значение силы тока и заряда на обкладках конденсатора соответственно равны Im = 1 А, qm = 10-6 Кл, то емкость C этого контура имеет значение … N18. Колебательный контур состоит из конденсатора емкостью С = 888 пФ и катушки с индуктивностью L = 2 мГн. На какую длину волны настроен контур? N19. Катушка с индуктивностью L = 30 мкГн присоединена к плоскому конденсатору с площадью пластин S = 0,01 м2 и расстоянием между ними d = 0,1 мм. Найти диэлектрическую проницаемость среды, заполняющей пространство между обкладками, если контур настроен на длину волны 750 м. N20. Складываются два гармонических колебания одного направления с одинаковыми периодами Т1=Т2=1,5с и амплитудами А1=А2=2 см. Начальные фазы колебаний j1=p/2 и j2=p/3. Определить начальную фазу и амплитуду результирующего колебания, написать его уравнение. N21. Написать уравнение результирующего колебания, возникающего при сложении двух колебаний одинаковых направлений и периода: х1=1Соspt см и х2=Cos(pt+p/2) см. N22. Напишите уравнение движения, получающегося в результате сложения двух одинаково направленных гармонических колебательных движений с одинаковым периодом Т = 8 с и одинаковой амплитудой А = 0,03 м. Разность фаз между этими колебаниями j2-j1 = 2p/3. Начальная фаза одного из этих колебаний равна нулю. N23. Складываются два гармонических колебания, происходящих в одном направлении: N24. Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями: x = 2cosp t см и y = 4sinp t см. Запишите уравнение траектории результирующего движения точки и постройте ее, указав направление движения N25. Точка совершает одновременно два гармонических колебания, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями x = 4cosp t см и y = 8cos(p t +p) см. Найдите уравнение траектории точки и постройте график ее движения. N26. Точка совершает одновременно два гармонических колебания, происходящих во взаимно перпендикулярных направлениях и выражаемых уравнениями х=А1Cos wt и y=A2Cos (wt+p). Найти уравнение траектории точки и построить график ее движения, если А1=4 см, A2= 8 см, w=p рад/c. N27. Точка совершает одновременно два гармонических колебания одинаковой частоты, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями: x = 2cosw t см и y = cosw t см. Запишите уравнение траектории результирующего движения точки и постройте ее с соблюдением масштаба. N28. Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями: x = 2sinp t см и y = - cosp t см. Запишите уравнение траектории результирующего движения точки и постройте ее, указав направление движения. N29. Определить период Т затухающих колебаний системы, если период собственных колебаний Т0=1с, а логарифмический декремент затухания l=0,628. N30. Амплитуда затухающих колебаний математического маятника за время t1=1мин уменьшилась вдвое. Во сколько раз уменьшится амплитуда за время t2=3 мин? N31. Найти логарифмический декремент затухания математического маятника, если за время t=1мин амплитуда колебаний уменьшилась в 2 раза. Длина маятника l =1 м. N32. Математический маятник длиной l =24,7 см совершает затухающие колебания. Через какое время t энергия колебаний уменьшится в 9,4 раза? Логарифмический декремент затухания l=1. N33. Логарифмический декремент затухания колебаний маятника l=0,003. Определить число N полных колебаний, которые должен сделать маятник, чтобы амплитуда колебаний уменьшилась в два раза. N34. Период затухающих колебаний Т=4 с, логарифмический декремент затухания l=1,6, начальная фаза равна нулю. При t=Т/4 смещение точки от положения равновесия х=4,5 см. Написать уравнение этого колебания. N35. Через какое время амплитуда колебаний, совершаемых пружинным маятником, уменьшится в 3 раза, если период T затухающих колебаний T = 4с, а логарифмический декремент затухания λ = 0,5? N36. Тело, совершающее затухающие колебания, за время N37. Колебательный контур состоит из конденсатора емкостью С=405нФ, катушки с индуктивностью L= 10 мГн, и сопротивления R=2 Ом. Во сколько раз уменьшится разность потенциалов на обкладках конденсатора за один период колебаний? N38. Колебательный контур состоит из катушки индуктивностью L=5,07 мГн и конденсатора емкостью С=0,2 мкФ. При каком логарифмическом декременте затухания l разность потенциалов на обкладках конденсатора за время t=1 мс уменьшится в 3 раза? Каково сопротивление контура? N39. Колебательный контур имеет емкость С=1,1 нФ, индуктивность L=5 мГн. Логарифмический декремент затухания l=0,005. За какое время вследствие затухания потеряется 99% энергии контура? N40. Определите логарифмический декремент затухания N41. Колебательный контур состоит из катушки с индуктивностью L = 2,5 мГн и конденсатора емкости C = 25 мкФ. При каком наименьшем значении сопротивления R кр контура в нем будет наблюдаться апериодический разряд, т.е. ω= 0? N42. Уравнение незатухающих колебаний дано в виде x=10Sin0,5pt см. 1). Написать уравнение волны, если скорость распространения колебаний vф=300 м/c. 2). Написать уравнение колебаний для точки, отстоящей от источника колебаний на расстоянии l =600м. N43. Уравнение незатухающих колебаний имеет вид x=Sin2,5pt см. Найти смещение от положения равновесия x, скорость v точки, находящейся на расстоянии l =20 м от источника колебаний, для момента времени t=1 c после начала колебаний. Скорость распространения колебаний vф=100 м /c. N44. Смещение от положения равновесия точки, отстоящей от источника колебаний на расстояние l1 = 4 см, в момент времени t1 = Т/ 6 равно половине амплитуды. Найти длину λ бегущей волны. N45. Волна с периодом Т=1,2 с и амплитудой А=2 см распространяется со скоростью vф=15 м /c. Чему равно смещение точки, отстоящей от источника волны на расстоянии l =45 м в тот момент, когда от начала колебаний источника прошло время t=4с? Чему равно максимальное значение скорости vm этой точки? N46. Определить скорость vф распространения волны в упругой среде, если разность фаз Dj двух точек среды, отстоящих друг от друга на расстояние Dх=10 см, равна p/3. Частота колебаний n=25 Гц. N47. Определить разность фаз N48. Найти разность фаз N49. Волна распространяется в упругой среде со скоростью
Волновая оптика
N1. На мыльную пленку (n=1,3), находящуюся в воздухе, падает нормально пучок лучей белого света. При какой наименьшей толщине пленки d отраженный свет с длиной волны l=550 нм окажется максимально усиленным в результате интерференции? N2. Пучок монохроматических световых волн (l=0,6 мкм) падает под углом i=300 на мыльную пленку (n=1,3). При какой наименьшей толщине d пленки отраженные лучи будут максимально ослаблены интерференцией? Максимально усилены? N3. На тонкий стеклянный клин (n=1,5) в направлении нормали к его поверхности падает монохроматический свет (l=600 нм). Определить угол g между поверхностями клина, если расстояние между соседними интерференционными минимумами в отраженном свете равно b=4 мм. N4. На тонкий стеклянный клин (n=1,55) падает нормально монохроматический свет. Двугранный угол g между поверхностями клина равен 2’. Определить длину световой волны l, если расстояние между соседними интерференционными максимумами в отраженном свете равно 0,3 мм. N5. Поверхности стеклянного клина (n=1,5) образуют между собой угол g=0,2’. На клин нормально к его поверхности падает пучок лучей монохроматического света с длиной волны l=0,55 мкм. Определить расстояние b между соседними интерференционными максимумами в отраженном свете. N6. Мыльная пленка, расположенная вертикально, образует клин вследствие стекания жидкости. При наблюдении интерференционных полос в отраженном монохроматическом свете (λ= 550 нм) оказалось, что расстояние между семью интерференционными полосами l = 28 мм. Найти угол γ клина. Свет падает перпендикулярно поверхности пленки. Показатель преломления мыльной воды n = 1,33.
N6. Мыльная пленка (n=1,33), расположенная вертикально, образует клин. Интерференция наблюдается в отраженном свете через красное стекло (l=631 нм). Расстояние между соседними красными полосами при этом равно а=3 мм. Затем эта же пленка наблюдается через синее стекло (l=400 нм). Найти расстояние между соседними синими полосами. Свет падает на пленку нормально. N8. Расстояние между первым и вторым темными кольцами Ньютона в отраженном свете равно l1=1 мм. Определить расстояние l2 между девятым и десятым кольцами. N9. На поверхность объектива (n = 1,7) нанесена тонкая прозрачная пленка с показателем преломления N10. Установка для получения колец Ньютона освещается монохроматическим светом с длиной волны l=589 нм, падающим по нормали к поверхности пластинки. Пространство между линзой и стеклянной пластинкой заполнено жидкостью. Найти показатель преломления n жидкости, если радиус третьего светлого кольца в проходящем свете r3=3,65 мм. Радиус кривизны линзы R=10 м. N11. Расстояние между пятым и двадцать пятым светлыми кольцами Ньютона равно 9 мм. Радиус кривизны линзы R=15 м. Найти длину волны монохроматического света, падающего нормально на установку. Наблюдение ведется в отраженном свете. N12. Установка для получения колец Ньютона освещается монохроматическим светом с длиной волны l=500 нм, падающим по нормали к поверхности пластинки. Пространство между линзой и стеклянной пластинкой заполнено водой (n=1,33). Найти толщину h слоя воды между линзой и пластинкой в том месте, где наблюдается третье светлое кольцо в отраженном свете. N13. Установка для получения колец Ньютона освещается светом с длиной волны l= 589 нм, падающим по нормали к поверхности пластинки. Пространство между линзой и стеклянной пластинкой заполнено жидкостью (n= 1,33). Найти радиус кривизны R линзы, если радиус третьего светлого кольца в проходящем свете равен r3 = 3,65 мм. N14. На установке для наблюдения колец Ньютона был измерен в отраженном свете радиус третьего темного кольца. Когда пространство между плоскопараллельной пластинкой и линзой заполнили жидкостью, тот же радиус стало иметь кольцо с номером, на единицу большим. Определить показатель преломления жидкости. N15. Плосковыпуклая линза выпуклой стороной лежит на стеклянной пластинке. Определить толщину h воздушного слоя между линзой и пластинкой в том месте, где в отраженном свете (l= 0,6 мкм) наблюдается четвертое светлое кольцо. N16. Дифракционная картина наблюдается на расстоянии l = 4 м от точечного источника монохроматического света (l=500 нм). Посередине между экраном и источником помещена диафрагма с круглым отверстием. При каком радиусе R отверстия центр дифракционных колец, наблюдаемых на экране, будет наиболее темным? N17. Радиус четвертой зоны Френеля для плоского волнового фронта равен 3мм. Определить радиус шестой зоны Френеля. N18. На диафрагму с радиусом отверстия R= 1 мм падает свет (l= 0,5 мкм) от точечного источника, находящегося на расстоянии a = 1 м от диафрагмы. Определите расстояние от диафрагмы до экрана, при котором в отверстии диафрагмы укладывается три зоны Френеля. N19. Свет от монохроматического источника (l=600 нм) падает нормально на диафрагму с диаметром отверстия d=6 мм. За диафрагмой на расстоянии b=3 м от нее находится экран. Какое число зон Френеля укладывается в отверстии диафрагмы? Каким будет центр дифракционной картины на экране: светлым или темным? N20. На диафрагму с круглым отверстием диаметра d=4 мм падает нормально параллельный пучок лучей монохроматического света (l=0,5 мкм). Точка наблюдения находится на оси отверстия на расстоянии b=1 м от него. Темное или светлое пятно получится в центре дифракционной картины, если в месте наблюдения поместить экран? N21. Плоская световая волна (l= 0,5 мкм) падает нормально на диафрагму с круглым отверстием диаметром d= 1 см. На каком расстоянии от отверстия должна находиться точка наблюдения, чтобы отверстие открывало одну зону Френеля? N22. На щель шириной a = 0,5 мм падает нормально монохроматический свет (l= 0,6 мкм). Определить угол между первоначальным направлением пучка света и направлением на четвертую темную дифракционную полосу. N23. На щель шириной a=0,1 мм нормально падает параллельный пучок света от монохроматического источника (l=0,6 мкм). Определить ширину центрального максимума в дифракционной картине, проецируемой с помощью линзы, находящейся непосредственно за щелью, на экран, находящийся на расстоянии L =1 м от линзы. N24. Сколько штрихов на каждый миллиметр содержит дифракционная решетка, если при наблюдении в монохроматическом свете (l=0,6 мкм) максимум пятого порядка отклонен на угол j=180? N25. Дифракционная решетка освещена нормально падающим монохроматическим светом. В дифракционной решетке максимум второго порядка отклонен на угол j1=140. Накакой угол j2 отклонен максимум третьего порядка? N26. Какое число штрихов на единицу длины n имеет дифракционная решетка, если зеленая линия ртути (l=546,1 нм) в спектре первого порядка наблюдается под углом j=1908’? N27. Дифракционная решетка содержит n= 200 штрихов на 1 мм. На решетку падает нормально монохроматический свет (λ= 600 нм). Максимум какого наибольшего порядка дает эта решетка? Чему равно общее число дифракционных максимумов? N28. На дифракционную решетку с числом n= 600 штрихов на 1мм рабочей длины решетки нормально падает параллельный пучок монохроматического света с длиной волны l=600 нм. Найдите угол jmax под которым наблюдается максимум наивысшего порядка. N29. При нормальном падении белого света на дифракционную решетку фиолетовая линия (l1= 400 нм) спектра k-го порядка видна под тем же углом дифракции, что и красная линия (l2= 600 нм) спектра другого порядка k1. Найдите минимальное значение k1 для красной линии. N30. Дифракционная решетка находится на расстоянии L= 3 м от экрана. При освещении ее нормально падающим монохроматическим светом с длиной волны l= 500 нм на экране получилась дифракционная картина, на которой второй главный максимум удален от центрального максимума на 0,6 м. Чему равна постоянная d решетки? N31.Во сколько раз уменьшится интенсивность естественного света, проходящего через поляризатор и анализатор, если угол j между плоскостями пропускания поляризатора и анализатора равен 600? N32. Найти угол между плоскостями пропускания поляризатора и анализатора, если интенсивность естественного света, проходящего через поляризатор и анализатор, уменьшается в 8 раз. N33. Интенсивность естественного света, проходящего через поляризатор и анализатор, уменьшается в 2,67 раза. Чему равен угол между плоскостями пропускания поляризатора и анализатора? N34. Угол j1 между плоскостями пропускания поляризатора и анализатора равен 450. Во сколько раз уменьшится интенсивность света, выходящего из анализатора, если угол увеличить до j2= 600? N35. Угол j1 между плоскостями пропускания поляризатора и анализатора равен 600. Во сколько раз увеличится интенсивность света, выходящего из анализатора, если угол уменьшить до j2= 300? N36. Пучок света, идущий в воздухе, падает на поверхность жидкости под углом i=540. Определить угол преломления пучка g, если отраженный пучок полностью поляризован. N37. Пучок естественного света падает на поверхность стеклянной пластины (n2=1,5), погруженной в жидкость. Отраженный от пластины пучок света составляет угол j=970 с падающим пучком. Определить показатель преломления жидкости n2, если отраженный свет полностью поляризован. N38. Предельный угол полного внутреннего отражения для некоторого вещества i = 450. Найти для этого вещества угол iб полной поляризации. Квантовая оптика 1. С поверхности сажи площадью S = 2 см2 при температуре Т = 400 К за время t = 5 мин излучается энергия W = 83 Дж. Найти отношение энергетических светимостей сажи и абсолютно черного тела для данной температуры. 2. Мощность N излучения шара радиусом R = 10 см при некоторой постоянной температуре Т равна 1,2 кВт. Найдите эту температуру, если отношение энергетических светимостей шара и абсолютно черного тела для данной температуры k = 0,25. 3. Температура вольфрамовой спирали в электрической лампочке мощностью 25 Вт равна 2450К. Отношение ее энергетической светимости к энергетической светимости абсолютно черного тела при данной температуре равно 0,3. Найти величину излучающей поверхности cпирали. 4. Определить энергию W, излучаемую за время t = 2 мин из смотрового окошка площадью S =10 см2 плавильной печи, если температура печи T = 1200 К. 5. Отношение энергетических светимостей угля и абсолютно черного тела при температуре Т = 600 К равно 0,8. Определите энергетическую светимость R угля и энергию W излучаемую с поверхности угля площадью S = 7 см2 за время t =12 мин. 6. Вследствие изменения температуры абсолютно черного тела максимум спектральной плотности энергетической светимости сместился с l1= 3,2 мкм на l2= 0,8 мкм. Как и во сколько раз изменились энергетическая светимость тела и максимальная спектральная плотность энергетической светимости? 7. Мощность излучения абсолютно черного тела N = 8 кВт. Найти площадь излучающей поверхности тела, если максимум спектральной плотности его энергетической светимости приходится на длину волны lm = 484 нм. 8. При увеличении термодинамической температуры T черного тела в два раза длина волны, на которую приходится максимум спектральной плотности энергетической светимости, уменьшилась на Dl = 400 нм. Определите начальную T 1 и конечную T 2 температуры тела. 9. При нагревании абсолютно черного тела длина волны, на которую приходится максимум спектральной плотности энергетической светимости, изменилась от 0,7 мкм до 0,45 мкм. Во сколько раз увеличилась при этом энергетическая светимость тела? 10. Абсолютно черное тело находится при температуре Т 1 = 2900 К. В результате остывания этого тела длина волны, на которую приходится максимум спектральной плотности энергетической светимости, изменилась на Dl = 9 мкм. До какой температуры Т 2 охладилось тело? 11. Какую мощность N надо подводить к зачерненному металлическому шарику радиусом 2 см, чтобы поддерживать его температуру на ΔТ = 27 К выше температуры окружающей среды Т = 293 К. Считать, что тепло теряется только в виде излучения. 12. Имеются два абсолютно черных источника теплового излучения, температура одного из них Т1 = 2500К. Найти температуру Т2 второго источника, если длина волны, отвечающая максимуму спектральной плотности его энергетической светимости, на Dl = 0,5 мкм больше длины волны, соответствующей максимуму спектральной плотности энергетической светимости первого источника. 13. Поверхность абсолютно черного тела нагрета до температуры Т = 1000 К. Затем одна половина этой поверхности нагревается на ΔТ = 100 К, другая охлаждается на ΔТ = 100 К. Во сколько раз изменится энергетическая светимость поверхности этого тела? 14. На поверхность металла падают монохроматические лучи с длиной волны l = 150 нм. Красная граница фотоэффекта l0 = 200 нм. Какая доля энергии фотона расходуется на сообщение электрону кинетической энергии? 15. Определить красную границу l0 фотоэффекта для цезия, если при облучении его поверхности фиолетовым светом с длиной волны l = 400 нм максимальная скорость фотоэлектронов равна 6,56×105 м/с. 16. На цинковую пластинку (Авых = 4,0 эВ) падает монохроматический свет с длиной волны l = 180 нм. Чему равен максимальный импульс фотоэлектронов? 17. При фотоэффекте с платиновой (Авых = 6,3 эВ) поверхности задерживающая разность потенциалов оказалась равной U = 0,9 В. Найдите частоту n применяемого излучения и красную границу n0 фотоэффекта. 18. Какая доля энергии фотона израсходована на работу вырывания фотоэлектрона, если красная граница фотоэффекта l0 = 300 нм. А максимальная кинетическая энергия фотоэлектрона равна 1 эВ? 19. На поверхность лития падает монохроматический свет (l = 310 нм). Чтобы прекратить эмиссию электронов нужно приложить задерживающую разность потенциалов U = 1,7 В. Определите красную границу l0 фотоэффекта. 20. Фотон с энергией e0 = 0,30 МэВ испытал комптоновское рассеяние на свободном электроне. Энергия рассеянного фотона e = 0,26 МэВ. Определите угол рассеяния q. 21. При эффекте Комптона энергия падающего фотона распределяется поровну между рассеянным фотоном и электроном отдачи. Угол рассеяния q = 900. Найти энергию e¢ и импульс p ¢ рассеянного фотона. 22. Рентгеновское излучение с длиной волны l0= 20 пм испытывает комптоновское рассеяние под углом q= 900. Найти изменение Dl длины волны рентгеновского излучения при рассеянии, а также энергию и импульс рассеянного фотона. 23. Фотон с энергией e = 250 кэВ испытал комптоновское рассеяние под углом q = 1200 на первоначально покоившемся свободном электроне. Определить энергию рассеянного фотона e¢. 24. Угол рассеяния фотона q = 900, угол отдачи электрона φ = 300. Определить энергию падающего фотона. 25. Фотон с длиной волны λ = 1 нм рассеялся на свободном электроне под углом q = 900. Какую долю своей энергии фотон передал электрону? 26. Определить угол q, на который был рассеян γ-квант с энергией e = 1,53 МэВ при эффекте Комптона, если кинетическая энергия электрона отдачи Wк = 0,51 МэВ. 27. Фотон с энергией e0 = 0,40 МэВ рассеялся под углом q = 900 на свободном электроне. Определить энергию рассеянного фотона, импульс и кинетическую энергию электрона отдачи. 28. Какая доля энергии фотона при эффекте Комптона приходится на электрон отдачи, если фотон претерпевает рассеяние на угол q = 1800? Энергия фотона до рассеяния e = 0,255 МэВ. 29. Определить импульс электрона отдачи при эффекте Комптона, если фотон с энергией равной энергии покоя электрона был рассеян на угол q = 1800. 30. Монохроматическое излучение с длиной волны λ = 500 нм падает нормально на плоскую зеркальную поверхность и давит на нее с силой F = 10 нН. Определить число фотонов N ежесекундно падающих на эту поверхность. 31. Параллельный пучок монохроматического света (λ = 662 нм) падает на зачерненную поверхность и производит на нее давление p = 0,3 мкПа. Определить концентрацию фотонов в световом пучке. 32. Давление монохроматического света (λ = 600 нм) на черную поверхность расположенную перпендикулярно лучам равно 0,1 мкПа. Определить число фотонов падающих за 1с на поверхность площадью 2см2. II. Атом Бора 1. Найти кинетическую энергию электрона, находящегося на второй орбите атома водорода. 2. Найти период и частоту обращения
|
||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 1048; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |


 см. Найти максимальную силу, действующую на точку и полную энергию колеблющейся точки.
см. Найти максимальную силу, действующую на точку и полную энергию колеблющейся точки.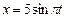 , см. В момент времени t, когда смещениеточки от положения равновесия x = 25 мм, скорость
, см. В момент времени t, когда смещениеточки от положения равновесия x = 25 мм, скорость  точки равна...
точки равна...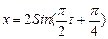 . Найти период колебаний, максимальную скорость и максимальное ускорение точки.
. Найти период колебаний, максимальную скорость и максимальное ускорение точки. . Найти моменты времени, в которые достигаются максимальная скорость и максимальное ускорение.
. Найти моменты времени, в которые достигаются максимальная скорость и максимальное ускорение. магнитного поля колебательного контура к энергии его электрического поля равно...
магнитного поля колебательного контура к энергии его электрического поля равно...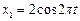 см и
см и  см. Напишите уравнение результирующего колебания.
см. Напишите уравнение результирующего колебания.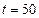 с потеряло 60% своей энергии. Определить коэффициент затухания
с потеряло 60% своей энергии. Определить коэффициент затухания 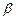 .
.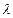 , при котором энергия колебательного контура за
, при котором энергия колебательного контура за  полных колебаний уменьшается в
полных колебаний уменьшается в  раз
раз колебаний источника волн, находящегося в упругой среде, и точки этой среды, отстоящей на расстоянии
колебаний источника волн, находящегося в упругой среде, и точки этой среды, отстоящей на расстоянии 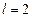 м от источника. Частота колебаний
м от источника. Частота колебаний 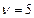 Гц, волны распространяются со скоростью
Гц, волны распространяются со скоростью  м/с.
м/с. м и
м и  м. Период колебаний
м. Период колебаний 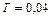 с; скорость распространения волны
с; скорость распространения волны  м/с.
м/с. м/c. Наименьшее расстояние
м/c. Наименьшее расстояние  между точками среды, фазы колебаний которых противоположны, равно 1м. Определить частоту колебаний.
между точками среды, фазы колебаний которых противоположны, равно 1м. Определить частоту колебаний.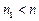 . Толщина пленки d = 0,11 мкм. На пленку нормально падают световые лучи с длиной волны l = 0,55 мкм. Показатель преломления пленки n 1 равен…
. Толщина пленки d = 0,11 мкм. На пленку нормально падают световые лучи с длиной волны l = 0,55 мкм. Показатель преломления пленки n 1 равен…


