
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поле на границе раздела диэлектриковСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В предыдущем параграфе мы предположили, что линии поля и направление вектора поляризации перпендикулярны к границе разделами тогда На границе двух диэлектриков с различными диэлектрическими проницаемостями
Дополнительное поле, создаваемое этими зарядами, перпендикулярно поверхности, поэтому нормальные составляющие полей
Векторы электростатического смещения в обеих средах соответственно равны
Аналогично рассмотренному выше случаю границы диэлектрик - вакуум нормальная составляющая вектора
Из этого выражения следует, что в случае
При переходе через границу раздела из диэлектрика с меньшим значением
Таким образом, при переходе через границу раздела двух диэлектриков изменяется не только вектор напряженности электрического поля 9. Энергия системы неподвижных точечных зарядов. Как мы уже знаем, электростатические силы взаимодействия консервативны; значит, система зарядов обладает потенциальной энергией. Будем искать потенциальную энергию системы двух неподвижных точечных зарядов Q1 и Q2, которые находятся на расстоянии r друг от друга. Каждый из этих зарядов в поле другого обладает потенциальной энергией (используем формулу потенциала уединенного заряда):
где φ12 и φ21 — соответственно потенциалы, которые создаются зарядом Q2 в точке нахождения заряда Q1 и зарядом Q1 в точке нахождения заряда Q2. Согласно,
поэтому W1 = W2 = W и
Добавляя к нашей системе из двух зарядов последовательно заряды Q3, Q4,..., можно доказать, что в случае n неподвижных зарядов энергия взаимодействия системы точечных зарядов равна
где φi — потенциал, который создается в точке, где находится заряд Qi, всеми зарядами, кроме i-го. Поле вблизи поверхности проводника. Выделим на поверхности S проводника площадку d S и построим на ней цилиндр с образующими, перпендикулярными к площадке d S, высотой d l (рис. 5.2).
На поверхности проводника вектор напряженности поля Поток вектора электрического смещения
Рис. 5.2 С другой стороны, по теореме Остроградского-Гаусса:
где σ – поверхностная плотность зарядов на d S. Из равенства правых частей следует, что
Итак, напряженность поля вблизи поверхности заряженного проводника прямо пропорцианальна поверхностной плотности зарядов. Электроёмкость. Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда q одного из проводников к разности потенциалов Δφ между ними:
В системе СИ единица электроемкости называется фарад (Ф):
Величина электроемкости зависит от формы и размеров проводников и от свойств диэлектрика, разделяющего проводники. Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства. Такие системы называются конденсаторами, а проводники, составляющие конденсатор, – обкладками.
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 834; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.47.194 (0.011 с.) |

 . В общем случае, когда линии поля не перпендикулярны к границе раздела это отношение остается справедливым лишь для нормальных составляющих вектора электрического смещения:
. В общем случае, когда линии поля не перпендикулярны к границе раздела это отношение остается справедливым лишь для нормальных составляющих вектора электрического смещения: 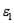 , и
, и 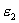 при наличии внешнего поля возникают поляризационные заряды разного знака с различными поверхностными плотностями зарядов
при наличии внешнего поля возникают поляризационные заряды разного знака с различными поверхностными плотностями зарядов 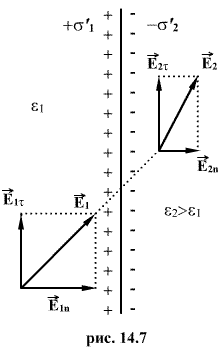
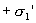 и
и  (рис.14.7).
(рис.14.7).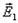 , и
, и  в обеих средах у границы раздела различны, а касательный составляющие одинаковы, т.е.
в обеих средах у границы раздела различны, а касательный составляющие одинаковы, т.е.
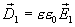 и
и 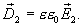
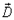 на границе двух диэлектриков
на границе двух диэлектриков  а отсюда следует, что
а отсюда следует, что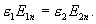
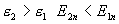 и линии вектора
и линии вектора 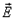 при переходе через границу раздела преломляются, отклоняясь от перпендикуляра к границе раздела. Из (14.11) и (14.12) следует, что
при переходе через границу раздела преломляются, отклоняясь от перпендикуляра к границе раздела. Из (14.11) и (14.12) следует, что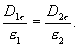 При
При 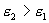 и
и 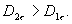
 в диэлектрик с большим значением
в диэлектрик с большим значением 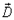 остается неизменной, а касательная увеличивается, так что линии вектора
остается неизменной, а касательная увеличивается, так что линии вектора 
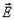 , но и вектор
, но и вектор  на границе раздела, равный по определению
на границе раздела, равный по определению 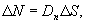 , с обеих сторон поверхности на основании
, с обеих сторон поверхности на основании 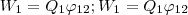
 и
и 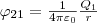

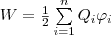 (1)
(1)
 и вектор электрического смещения
и вектор электрического смещения 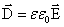 перпендикулярны поверхности. Поэтому поток
перпендикулярны поверхности. Поэтому поток 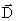 сквозь боковую поверхность равен нулю.
сквозь боковую поверхность равен нулю.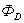 через
через 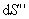 тоже равен нулю, так как
тоже равен нулю, так как 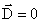 лежит внутри проводника, где
лежит внутри проводника, где 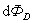 и, следовательно,
и, следовательно, 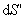 . Отсюда следует, что поток
. Отсюда следует, что поток  сквозь замкнутую поверхность равен потоку
сквозь замкнутую поверхность равен потоку 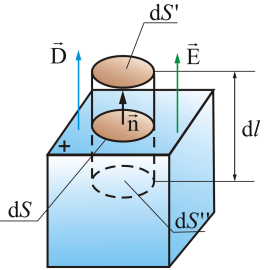
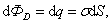
 , тогда
, тогда .
.





