
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон сохранения электрического заряда. Электростатическое поле. Напряжённость электростатического поля. Силовые Линии.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Закон сохранения электрического заряда. Электростатическое поле. Напряжённость электростатического поля. Силовые линии. В любой электрически изолированной системе алгебраическая сумма зарядов не изменяется, это утверждение выражает закон сохранения электрического заряда. Электростатическое поле — поле, созданное неподвижными в пространстве и неизменными во времени электрическими зарядами (при отсутствии электрических токов). силовыми линиями – это линии, касательная к которым в любой точке поля совпадает с направлением вектора напряженности
Напряженность электростатического поля. Принцип суперпозиции. Взаимодействие между зарядами осуществляется через поле. Всякий электрический заряд q изменяет определенным образом свойства окружающего его пространства – создает электрическое поле. Это поле проявляет себя в том, что помещенный в какую-либо его точку другой, «пробный» заряд испытывает действие силы. Опыт показывает, что сила может быть представлена, как F=q’E, Где вектор E называют напряженностью электрического поля в данной точке. E можно определить как силу, действующую на единичный положительный неподвижный заряд. Напряженность поля системы точечных неподвижных зарядов равна векторной сумме напряженностей полей, который создавали бы каждый из зарядов в отдельности.
Поток вектора напряженности электрического поля. По определению потоком векторного поля
Тогда поток через всю поверхность S будет:
Заметим, что поток – величина алгебраическая. Знак потока зависит от выбора направления нормали к элементарным площадкам, на которые разбивается поверхность S при вычислении ФЕ. Изменение направления нормали на противоположное изменит знак En, а значит и знак потока ФЕ. В случае замкнутых поверхностей принято считать знак потока положительным, если силовые линии поля выходят из охватываемой области наружу. Численно поток равен количеству силовых линий, пресекающих данную поверхность.Размерность потока в СИ: [ФЕ] = В·м (отметим, что она совпадает с размерностью величины q/εо). 3. Теорема Гаусса в интегральной и дифференциальной формах в вакууме и ее применение для расчета электрических полей Теорема Гаусса Поток вектора напряжённости электрического поля через любую, произвольно выбранную, замкнутую поверхность равен алгебраической сумме заключённых в этой поверхности электрических зарядов, делённой на электрическую постоянная ε0:
Данное выражение представляет собой теорему Гаусса в интегральной форме. В дифференциальной форме теорема Гаусса выражается следующим образом:
где ρ — объёмная плотность заряда
Работа электростатического поля при перемещении зарядов. Циркуляция вектора напряженности. Работа электростатического поля (A)
A = Fd=qEd,
A1 = Fd1 cos , но d1 cos = d, A1 = qEd A = A1 A1,2,3,1 = A1,2 + A2,3 + A3,1
A1,2,3,1 = qEd1 cos a + Eqh cos 90° + Eqd cos 180° = qEd + 0 + (- qEd) A1,2,3,1 =0 т. е. работа при перемещении заряда между двумя точками в электростатическом поле не зависит от формы траектории, а зависит от положения этих точек. Работа по замкнутой траектории равна нулю.
Из принципа суперпозиции следует, что работа электростатических сил над зарядом, перемещаемым по замкнутому контуру, равна 0: Для любого контура в электростатическом поле циркуляция напряженности – тождественный нуль. Напряженность электростатического поля (с точностью до знака) может быть истолкована как градиент некоторой функции координат, называемой потенциалом электростатического поля Уравнение Пуассона. Проблема расчета электростатического поля в общем случае не является безнадежной. Действительно, если вспомнить выражение векторного поля через потенциал электростатического поля То есть Подставив (1.65) в
Поляризация диэлектриков. Поляризация диэлектриков — явление, связанное с ограниченным смещением связанных зарядов в диэлектрике или поворотом электрических диполей, обычно под воздействием внешнего электрического поля, иногда под действием других внешних сил или спонтанно. Диэлектрик, помещенный во внешнее электрическое поле, поляризуется под действием этого поля. Поляризацией диэлектрика называется процесс приобретения им отличного от нуля макроскопического дипольного момента. Степень поляризации диэлектрика характеризуется векторной величиной, которая называется поляризованостью или вектором поляризации (P). Поляризованность определяется как электрический момент единицы объема диэлектрика
где N - число молекул в объеме. Поляризованность P часто называют поляризацией, понимая под этим количественную меру этого процесса. В диэлектриках различают следующие типы поляризации: электронную, ориентационную и решеточную (для ионных кристаллов). Электронный тип поляризации
Индуцированный дипольный момент молекулы пропорционален напряженности внешнего электрического поля где Решеточный тип поляризации
Поляризованность изотропных диэлектриков любого типа связана с напряженностью поля соотношением Поляризованность Диэлектрик, помещенный во внешнее электрическое поле, поляризуется под действием этого поля. Поляризацией диэлектрика называется процесс приобретения им отличного от нуля макроскопического дипольного момента. Степень поляризации диэлектрика характеризуется векторной величиной, которая называется поляризованостью или вектором поляризации (P). Поляризованность определяется как электрический момент единицы объема диэлектрика
где N - число молекул в объеме В диэлектриках различают следующие типы поляризации: электронную, ориентационную и решеточную (для ионных кристаллов).
Индуцированный дипольный момент молекулы пропорционален напряженности внешнего электрического поля Ориентационнный тип поляризации характерен для полярных диэлектриков. В отсутствие внешнего электрического поля молекулярные диполи ориентированы случайным образом, так что макроскопический электрический момент диэлектрика равен нулю.
Если поместить такой диэлектрик во внешнее электрическое поле, то на молекулу-диполь будет действовать момент сил (рис. 2.2), стремящийся ориентировать ее дипольный момент в направлении напряженности поля. Однако полной ориентации не происходит, поскольку тепловое движение стремится разрушить действие внешнего электрического поля. Такая поляризация называется ориентационной. Поляризованность в этом случае равна Решеточный тип поляризации характерен для ионных кристаллов. В ионных кристаллах (NaCl и т.д.) в отсутствие внешнего поля дипольный момент каждой элементарной ячейки равен нулю (рис. 2.3.а), под влиянием внешнего электрического поля положительные и отрицательные ионы смещаются в противоположные стороны (рис. 2.3.б). Каждая ячейка кристалла становится диполем, кристалл поляризуется. Такая поляризация называется решеточной. Поляризованность и в этом случае можно определить как
Поляризованность изотропных диэлектриков любого типа связана с напряженностью поля соотношением Электроёмкость. Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда q одного из проводников к разности потенциалов Δφ между ними:
В системе СИ единица электроемкости называется фарад (Ф):
Величина электроемкости зависит от формы и размеров проводников и от свойств диэлектрика, разделяющего проводники. Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства. Такие системы называются конденсаторами, а проводники, составляющие конденсатор, – обкладками. Уравнение непрерывности. Представим себе, в некоторой проводящей среде, где течет ток, замкнутую поверхность S. Для замкнутых поверхностей векторы нормалей, а следовательно, и векторы
Из (7.3.1) и постоянства значения I во всех участках цепи постоянного тока следует, что плотности постоянного тока в различных поперечных сечениях 1 и 2 цепи обратно пропорциональны площадям
Пусть S – замкнутая поверхность, а векторы
Это соотношение называется уравнением непрерывности. Оно является, по существу, выражением закона сохранения электрического заряда. Дифференциальная форма записи уравнения непрерывности записывается так:
В случае постоянного тока, распределение зарядов в пространстве должно оставаться неизменным:
это уравнение непрерывности для постоянного тока (в интегральной форме). Линии
Закон Ома. Для однородного участка цепи: Сила тока, текущего по однородному металлическому проводнику,пропорциональна разности потенциалов на его концах I=U/R; R=P*l/s,где Р- удельное электрическое сопротивление, l-длина проводника, s-площадь поперечного сечения проводника.
Найдем связь между В изотропном проводнике (в данном случае с постоянным сопротивлением) носители зарядов движутся в направлении действия силы, т.е. вектор плотности тока
Рис. 7.6 Исходя из закона Ома (7.6.1), имеем:
это запись закона Ома в дифференциальной форме.
При замкнутой внешней цепи сумма падений электрических потенциалов и эдс источника равна сумме падений напряжения на внутреннем сопротивлении источника и во всей внешней цепи. Закон Джоуля –Ленца: Количество теплоты, выделяемое постоянным электрическим током на участке цепи, равно произведению квадрата силы тока на время его прохождения и электрическое сопротивление этого участка цепи. В интегральной форме этот закон имеет вид
где dQ — количество теплоты, выделяемое за промежуток времени dt, I — сила тока, R — сопротивление, Q — полное количество теплоты, выделенное за промежуток времени от t1 до t2. Введем плотность тепловой мощности
с учетом закона Ома в дифференциальной форме
Взаимная индукция. Возьмем два контура, расположенные недалеко друг от друга, как это показано на рисунке 5.4.
Рис. 5.4 В первом контуре течет ток
При изменении тока
Аналогично, ток
И при изменении тока
Контуры называются связанными, а явление – взаимной индукцией. Коэффициенты Трансформатор является типичным примером двух связанных контуров. Рассмотрим индуктивность трансформатора и найдем коэффициент трансформации. Вихревые токи Индукционные токи в массивных проводниках называюттоками Фуко. Токи Фуко могут достигать очень больших значений, т.к. сопротивление массивных проводников мало.Поэтому сердечники трансформаторов делают из изолированных пластин. Закон сохранения электрического заряда. Электростатическое поле. Напряжённость электростатического поля. Силовые линии. В любой электрически изолированной системе алгебраическая сумма зарядов не изменяется, это утверждение выражает закон сохранения электрического заряда. Электростатическое поле — поле, созданное неподвижными в пространстве и неизменными во времени электрическими зарядами (при отсутствии электрических токов). силовыми линиями – это линии, касательная к которым в любой точке поля совпадает с направлением вектора напряженности
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 844; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.124.52 (0.011 с.) |

 (рис. 2.1).
(рис. 2.1). Силовой линии приписывают определенное направление – от положительного заряда к отрицательному, или в бесконечность.
Силовой линии приписывают определенное направление – от положительного заряда к отрицательному, или в бесконечность.
 через площадку
через площадку  называется величина (рис.2.1)
называется величина (рис.2.1)
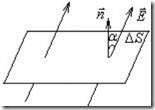 Если поле неоднородно или поверхность, через которую вычисляется поток, не является плоской то определение потока нужно применить кбесконечно малому элементу поверхности, а именно записать:
Если поле неоднородно или поверхность, через которую вычисляется поток, не является плоской то определение потока нужно применить кбесконечно малому элементу поверхности, а именно записать:


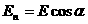 .
. .
. ,
,
 .
.
 .
. :
: .
. (1.65)
(1.65) 
 получаем:
получаем: Уравнение Пуассона.
Уравнение Пуассона.


 - поляризуемость молекулы. Значение поляризованности в этом случае равно
- поляризуемость молекулы. Значение поляризованности в этом случае равно  , где n - концентрация молекул;
, где n - концентрация молекул;  - индуцированный дипольный момент молекулы, который одинаков для всех молекул и направление которого совпадает с направлением внешнего поля.
- индуцированный дипольный момент молекулы, который одинаков для всех молекул и направление которого совпадает с направлением внешнего поля.
 , где
, где 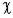 - диэлектрическая восприимчивость диэлектрика.
- диэлектрическая восприимчивость диэлектрика. ,
, . Поляризованность P часто называют поляризацией, понимая под этим количественную меру этого процесса.
. Поляризованность P часто называют поляризацией, понимая под этим количественную меру этого процесса.
 , где
, где  - поляризуемость молекулы. Значение поляризованности в этом случае равно
- поляризуемость молекулы. Значение поляризованности в этом случае равно  , где n - концентрация молекул
, где n - концентрация молекул  ;
;  - индуцированный дипольный момент молекулы, который одинаков для всех молекул и направление которого совпадает с направлением внешнего поля.
- индуцированный дипольный момент молекулы, который одинаков для всех молекул и направление которого совпадает с направлением внешнего поля.
 , где < p > - среднее значение составляющей дипольного момента молекулы в направлении внешнего поля.
, где < p > - среднее значение составляющей дипольного момента молекулы в направлении внешнего поля. , где
, где  - значение дипольного момента элементарной ячейки, n - число ячеек в единице объема.
- значение дипольного момента элементарной ячейки, n - число ячеек в единице объема. 
 , где
, где  - диэлектрическая восприимчивость диэлектрика.
- диэлектрическая восприимчивость диэлектрика.

 принято брать наружу, поэтому интеграл
принято брать наружу, поэтому интеграл 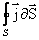 дает заряд, выходящий в единицу времени наружу из объема V, охваченного поверхностью S. Мы знаем, что плотность постоянного электрического тока одинакова по всему поперечному сечению S однородного проводника. Поэтому для постоянного тока в однородном проводнике с поперечным сечением S сила тока:
дает заряд, выходящий в единицу времени наружу из объема V, охваченного поверхностью S. Мы знаем, что плотность постоянного электрического тока одинакова по всему поперечному сечению S однородного проводника. Поэтому для постоянного тока в однородном проводнике с поперечным сечением S сила тока: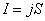
 и
и  этих сечений (рис. 7.2):
этих сечений (рис. 7.2): .
.

 . Тогда поток вектора
. Тогда поток вектора  сквозь эту поверхность S равен электрическому току I, идущему вовне из области, ограниченный замкнутой поверхностью S. Следовательно, согласно закону сохранения электрического заряда, суммарный электрический заряд q, охватываемый поверхностью S, изменяется за время
сквозь эту поверхность S равен электрическому току I, идущему вовне из области, ограниченный замкнутой поверхностью S. Следовательно, согласно закону сохранения электрического заряда, суммарный электрический заряд q, охватываемый поверхностью S, изменяется за время  на
на  , тогда в интегральной форме можно записать:
, тогда в интегральной форме можно записать: .
.
 или
или 
 следовательно,
следовательно,
 . Если ток постоянный, то избыточный заряд внутри однородного проводника всюду равен нулю. В самом деле, т.к. для постоянного тока справедливо уравнение
. Если ток постоянный, то избыточный заряд внутри однородного проводника всюду равен нулю. В самом деле, т.к. для постоянного тока справедливо уравнение  , то
, то Избыточный заряд может появиться только на поверхности проводника в местах соприкосновения с другими проводниками, а также там, где проводник имеет неоднородности.
Избыточный заряд может появиться только на поверхности проводника в местах соприкосновения с другими проводниками, а также там, где проводник имеет неоднородности. – удельная электропроводность. Размерность σ – [
– удельная электропроводность. Размерность σ – [  ].
]. в бесконечно малом объеме проводника – закон Ома в дифференциальной форме.
в бесконечно малом объеме проводника – закон Ома в дифференциальной форме.
 А мы знаем, что
А мы знаем, что  или
или  . Отсюда можно записать
. Отсюда можно записать ,
,
 - закон ома в интегральной форме
- закон ома в интегральной форме

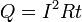
 , равную энергии выделенной за единицу время прохождения тока в каждой единице объема проводника
, равную энергии выделенной за единицу время прохождения тока в каждой единице объема проводника где S - поперечное сечение проводника,
где S - поперечное сечение проводника,  - его длина. Используя (1.13) и соотношение
- его длина. Используя (1.13) и соотношение  , получим
, получим
 - плотность тока, а
- плотность тока, а 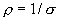 , тогда
, тогда
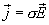 , окончательно получаем
, окончательно получаем

 . Он создает магнитный поток, который пронизывает и витки второго контура.
. Он создает магнитный поток, который пронизывает и витки второго контура. ,
,
 ,
,
 второго контура создает магнитный поток, пронизывающий первый контур:
второго контура создает магнитный поток, пронизывающий первый контур: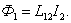 ,
,
 ,
,
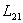 и
и  называются взаимной индуктивностью, или коэффициентами взаимной индукции. Причём
называются взаимной индуктивностью, или коэффициентами взаимной индукции. Причём 



