
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Энергетические характеристики электрического поляСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
(Потенциал электрического поля) Работа сил электростатического поля.
dA=
dA= так как dr=cosα.ds
Эта работа определяется только начальным и конечным положением пробного заряда q0,т.е. электрическое поле является потенциальным, а кулоновские силы - потенциальными или консервативными (как гравитационные силы). Тогда работа A1→2 перемещения заряда q0 из точки 1 до точки 2 равна убыли потенциальной энергии Wp: Принимается Wp (r→∞)=0, тогда С=0.
φ = работе, совершаемой полем при перемещении единичного, положительного заряда из этой точки поля до бесконечности (∞). Единица измерения потенциала [ φ ] = Вольт (В); 1В = Т.е. Вольт является потенциалом такой точки, при перемещении из которой заряд +1 Кл на бесконечность, совершается 1 Дж работа.
Теперь уже можно найти, что В атомной физике, астрофизике и химии за единицу энергии обычно употребляется электрон-вольт (эв). За 1эв принимается такое количество энергии, которая приобретает электрон пройдя разность потенциалов Δφ=1в. 1 эв=1,6.10-19 Кл. 1 в=1,6.10-19Дж Для сравнения; энергия теплового движения молекул при комнатной температуре (Т≈300К0) Таким образом,
Если q0 заряд перемещается из точки с потенциалом φ1 в точку с потенциалом φ2, то силы поля совершают такую работу. Иными словами, разность потенциалов двух точек поля равна работе сил поля по перемещению единичного, положительного заряда из одной точки в другую. Из Wp (r→∞)=0 вытекает, что и φ(∞)=0, но это несущественно, т.к. важна Δφ:в формулах, обычно, присутствует именно разность потенциалов. Знак потенциала определяется знаком заряда, создающего поля, таким образом, потенциал поля точечного заряда (или шара с однородным распределением зарядов при r>R, где R -радиус шара):
где (-) относится к случаю отрицательного заряда а (+) к случаю положительного заряда. Если q<0, то силы поля препятствуют перемещению единичного положительного (+) заряда на бесконечность, совершая тем самым отрицательную работу. Поэтому потенциал любой точки поля созданного отрицательным зарядом, является отрицательным (подобно тому, как отрицателен гравитационный потенциал любой точки поля тяготения). Если же q<0, то силы поля сами перемещают единичный (+) заряд на бесконечность, совершая положительную работу. Поэтому потенциал любой точки поля +q является положительным. Принцип суперпозиции для потенциалов, создаваемые несколькими зарядами, означает, что потенциал φ результирующего поля равен алгебраической сумме потенциалов полей всех этих зарядов (так как потенциал поля скалярная величина): φ=φ1+φ2+φ3+…+φn = Потенциальная энергия отталкивания одноименных зарядов > 0 и возрастает при сближении зарядов. Потенциальная энергия разноименных зарядов отрицательна и возрастает до нуля при удалении одного из зарядов в бесконечность. Работа электрических сил отталкивания одноименных зарядов положительна, если заряды удаляют друг от друга, и отрицательна, если происходит сближение зарядов. Иными словами, работа электростатических сил притяжения разноименных зарядов положительна, если заряды сближаются и отрицательна, если они удаляются друг от друга.
Всякая конфигурация покоящихся электрических зарядов неустойчива, если между ними действуют только кулоновские силы (теорема Ирншоу). Или иными словами, устойчивое статическое распределение электрических зарядов, находящихся на конечных расстояниях друг от друга, невозможно. Надо отметить, что равновесие между многими разноименными зарядами может осуществляться при определенном их взаиморасположении и определенном соотношении между их величинами. Но это равновесие не будет устойчивым.
Механический аналог устойчивого и неустойчивого равновесия шарик в гравитационном поле.
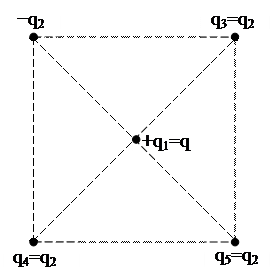
Пример неустойчивого равновесия q2=q3=q4=q5=−4(2√2-1)q/7≈1,04 q
Устойчивое равновесие заряженных частиц в атомах, молекулах, ионах и т. п. системах достигается благодаря динамическому характеру их взаимодействии, т.е. они не являются статическими системами. Например, динамический (колебательный) характер устойчивости в молекулах приводит к одновременным действием межмолекулярных сил притяжения и отталкивания, причем зависимость сил притяжения и сил отталкивания от расстояния между заряженными частицами выражается различными и отличающимися от закона Кулона закономерностями. Поверхность, во всех точках которой потенциал одинаков, называется эквипотенциальной поверхностью: перемещение заряда вдоль этой поверхности не сопровождается работой, так как при φ=const, Δφ=0. А это значит, что в каждой точке силовые линии электрического поля перпендикулярны эквипотенциальным поверхностям.
Свойства электростатических полей: 1. В каждой точке эквипотенциальной поверхности напряженность 2. Работа по перемещению электрического заряда по одной и той же эквипотенциальной поверхности равняется 0. Например Внутри проводника Таким образом, электрическое поле графически можно изображать не только при помощи силовых линий, но и при помощи эквипотенциальных поверхностей: они обычно проводят так, чтобы Δφ между любыми двумя соседними эквипотенциальными поверхностями были одинаковыми. Связь между напряженностью и потенциалом электрического поля
По сущности, эта связь между силовыми и энергетическими характеристиками электрического поля.
dA=q0Edℓ.cosα dA=q0(φ1-φ2)=- q0(φ2-φ1)= -q0dφ учитывая, что dℓ .cosα=dn
Модуль напряженности поля (Е) в данной точке определяется быстротой падения потенциала вдоль линии напряженности. Знак (-) показывает, что вектор направлен в сторону убывания потенциала.
Градиент физической величины называется ее изменение, приходящееся на единицу расстояния в направлении наибольшего возрастания: Понятие градиента применимо к любой физической величине (скорости, плотности, температуре, давлению и т.д.), если только она имеет пространственное распределение. Например, известно, что средний градиент температуры земной коры (геотермический градиент) направлен к центру Земли и составляет около 0,003 К/м. Это означает, что температура земной коры возрастает в среднем на 30С на каждые 100м глубины. В общем случае Таким образом,
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 2850; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.29.209 (0.009 с.) |

 Элементарная работа как скалярное произведение
Элементарная работа как скалярное произведение =F.cosα .ds
=F.cosα .ds

 . Сравнивая с А12 для выражения потенциальной энергии получаем:
. Сравнивая с А12 для выражения потенциальной энергии получаем:  .
. Не зависит от значения пробного заряда q0 и служит энергетической характеристикой электрического поля (потенциал электрического поля).
Не зависит от значения пробного заряда q0 и служит энергетической характеристикой электрического поля (потенциал электрического поля). ;
;


 =
=  . Сравнивая с А12 или А1→2 и разделяя на q0
. Сравнивая с А12 или А1→2 и разделяя на q0 ,
,
 Так как эти потенциальные кривые не имеют минимума (потенциальной ямы), то эта система не может находиться в устойчивом равновесии, т.е. она неустойчива.
Так как эти потенциальные кривые не имеют минимума (потенциальной ямы), то эта система не может находиться в устойчивом равновесии, т.е. она неустойчива.
 Противовес электрических сил в моделях атомов, молекул, ионов, в кристаллах существуют непрерывное движение и колебание заряженных частиц.
Противовес электрических сил в моделях атомов, молекул, ионов, в кристаллах существуют непрерывное движение и колебание заряженных частиц.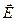 перпендикулярна к этой поверхности и направлена в сторону убывания потенциала.
перпендикулярна к этой поверхности и направлена в сторону убывания потенциала.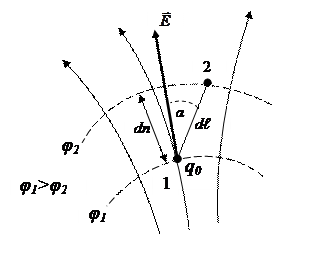 На рисунке нанесены силовые линии (сплошные стрелки) и проекции эквипотенциальных поверхностей (пунктирные линии) электростатического поля. Элементарная работа, совершаемая полем при передвижении заряда q0 из точки 1 в точку 2, можно определить двумя способами:
На рисунке нанесены силовые линии (сплошные стрелки) и проекции эквипотенциальных поверхностей (пунктирные линии) электростатического поля. Элементарная работа, совершаемая полем при передвижении заряда q0 из точки 1 в точку 2, можно определить двумя способами:
 ,
, .
. , который обозначается также оператором Гамильтона или «набла»- оператором (
, который обозначается также оператором Гамильтона или «набла»- оператором ( U).
U). =− grand φ.
=− grand φ.


