
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обратимый процесс есть идеализированная модель реальных процессов, необходимая для успешного изучения последних.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Изопроцессами (от слово изос - одинаковый) называются термодинамические процессы, протекающие в системе с неизменной массой при постоянном значении одного из параметров состояния системы: температуры (Т), давления (р) или объема (V). Изотермическим (изотермным) процессом называется термодинамический процесс, протекающий при неизменной температуре (T=const). Изобарическим (изобарным) называется процесс, при котором давление сохраняется постоянным (p=const). Изохорическим (изохорным) называется термодинамический процесс, протекающий при постоянном объеме системы (V=const).
Экспериментально для изопроцессов были установлены следующие газовые законы. · Закон Бойля – Мариотта (1679г.) Для данной массы газа (m=const) при постоянной температуре (T=const) давление газа изменяется обратно пропорционально его объему: pV=const. На рис.1 изображена зависимость p от V в виде изотерм, т.е. линии (гиперболы) одинаковых температур. · Законы Гей-Люссака (1802г.) 1. Объем данной массы при постоянном давлении изменяется линейно с температурой: V=V0 (1+αt) при p=const, m=const (рис.2, а)). 2. Давление данной массы газа при постоянном объеме изменяется линейно с температурой (иногда называют законом Шарля (1787г.)): p=p0 (1+αt) при V=const, m=const (рис. 2, б)). В этих уравнениях t − температура по шкале Цельсия, p и V давление и объем газа при температуре t0C, p0 и V0 - давление и объем при 0 0С, коэффициент α =1/273,15 К -1 и называется коэффициентом объемного расширения газа или термическим коэффициентом давления газа.
При t ≈ – 273 0 С, V= 0 (на рис.2 а)) или p= 0 (на рис.2 б)), котороеуказывает границы применения этих законов. Учитывая, что T=273,15+t, можно получить: V1/V2 =T1/ T2 , или V=V0αT, при p=const, m=const; т.е. V~T. p1 / p2 =T1 / T2, или p=p0αT, при V=const, m=const; т.е. p~T. При T=0 прекращается хаотическое движение молекул, но не движение электронов в атоме. Для некоторой массы газа m существует определенная связь между p, V, T, называемая уравнением состояния. f(p, V, T)=0, где каждая из переменных является функцией двух других.
Переход из состояния 1→2 происходит двумя процессами: 1→1 ′ (изотермический) и 1′→2 (изохорный), для которых справедливы p1V1=p1′V2 и p1′/p2=T1/T2. Исключив p1′, получаем Т.к. точки 1 и 2 произвольны, то это равенство справедливо всегда, для всех точек и для данной массы газа.
где В – газовая постоянная, зависящая от массы и типа газа. Менделеев объединил уравнение Клапейрона с законом Авогадро, отнеся это уравнение к одному молю, использовав молярный объем Vm. Согласно закону Авогадро, при одинаковых p и T моли всех газов занимают одинаковый молярный объем Vm, поэтому постоянная B будет уже одинакова для всех идеальных газов. Эта общая для всех газов постоянная обозначается R и называется универсальной или молярной газовой постоянной. pVm=RT или, учитывая (1), где R=8,31 Дж/(моль·К), n − количество вещества в мольях. Уравнение (2) называется уравнением Клапейрона − Менделеева или уравнением состояния идеального газа. (Можно вывести уравнения Клапейрона − Менделеева из законов Бойля – Мариотта и Гей-Люссака, используя другие комбинации изопроцессов при переходе от одной произвольной точки (pV) пространства к другой произвольной точке). Часто используют постоянную Больцмана (k): k=R/NA=1,38∙10−23Дж/К. Тогда из pVm=RT → p=RT/Vm=kNAT/Vm=N∙kT где N=NA/Vm − концентрация молекул (число частиц в единице объема). Из p=N∙kT, видно, чтодавление идеального газа при данной температуре p ~ N − концентрации или плотности газа. При одинаковых температуре и давлении все газы содержат в единице объема одинаковое число молекул. Число молекул, содержащихся в 1м газа при нормальных условиях, называется числом Лошмидта:
§ 3. Уравнение состояния реальных газов
Реальные газы по своим свойствам близки к модели идеальных газов при нормальных условиях, а также при достаточно высоких температурах и низких давлениях. Например, в 1м3 газа, при нормальных условиях, содержится 2,68∙1025 молекул, занимающие 2,68∙1025∙(10−10)3≈10−4м3<<1м3 объем. При давлении 500МПа (1атм=101,3кПа) объем молекул уже Vмолекул≈ 0,5м3. Поэтому для реальных газов в уравнении состоянии надо учитывать собственный объем молекул и силы межмолекулярного взаимодействия.
Силы межмолекулярного взаимодействия (силы Ван-дер-Ваальса) − короткодействующие: они преобладают на расстояниях ≤10−9м и быстро убывают при r→∞.
Между молекулами тела одновременно действуют силы взаимного притяжения (сцепления) (fпр) и силы взаимного отталкивания (fот).
Как видно, эти силы (особенно силы отталкивания) очень быстро убывают с увеличением расстояниями между молекулами. На расстоянии r>>r0 силы притяжении стремятся возвращать частицы, компоненты молекул, прежнее состояние, при r<r0 силы отталкивания препятствуют дальнейшему сжатию. На графике Wp (r) Потенциальной энергии взаимодействия двух молекул (рис. 4), которая составляет часть энергии этой системы, представлена потенциальная кривая этой зависимости. Участок АВС это потенциальная яма где точка В – дно ямы, а DB – глубина потенциальной ямы или высота потенциального барьера. Величина Wp (r) измеряется той работой, которая совершается силой F(r), при изменении расстояния между молекулами от r до ∞, где Wp( ∞ )=0 (на ∞ две молекулы не взаимодействуют). Устойчивое равновесие соответствует Wp(min) на расстоянии r0≈3.10−10м. Таким образом, система из двух взаимодействующих молекул в состоянии устойчивого равновесия (r=r0) обладает минимальной потенциальной энергией Wp(min). Агрегатное состояние вещества можно характеризовать средней кинетической энергией Если Wp(min)<<kT,. вещество газообразное, т.к. тепловое движение препятствует соединению молекул. Если Wp(min)>>kT,. вещество твердое, т.к. молекулы притягиваясь друг к другу, не могут удалиться на значительное расстояние и колеблются около r=r0. Если же Wp(min)≈kT,. то вещество находится в жидком состоянии, т.к. в результате теплового движения молекулы перемещаются в пространстве, обмениваясь местами, но не расходясь на расстояние r>r0/ Таким образом, любое вещество в зависимости от T может находиться в газообразном, жидком и твердом агрегатном состояниях, причем эта температура T зависит от Wp(min) для данного вещества.
Уравнение ВАН-ДЕР-ВААЛЬСА или уравнение состояния реальных газов Как уже отмечалось, при низких температурах или высоких давлениях, когда молекулы газа находятся близко друг от друга, пренебрегать их размерами и силами межмолекулярного взаимодействия уже недопустимо.
1. Учет собственного объема молекул. Из-за собственного объема фактический свободный объем, в котором могут двигаться молекулы реального газ, уменьшится и будет Vm−b, где b – объем, занимаемый самыми молекулами. Недоступный объем b равен учетверенному собственному объему молекул.
2. Учет притяжения молекул приводит к появлению дополнительного давления на газ (внутреннее давление) p'=a/Vm2, где а – постоянная Ван-дер-Ваальса, характеризующая силы межмолекулярного притяжения, Vm – молярный объем . Таким образом, вводя эти поправки, уравнение состояния реальных газов, или уравнение Ван-дер-Ваальса, для моля газа имеет вид:
(p+a/Vm2)(Vm−b)=RT (2) Или для произвольного количества вещества n газа (т.к. n=m/M и V=nVm)
где a и b постоянные, которые для каждого газа определяются опытном путем. Из (2) видно, что в зависимости p=f(V), V присутствует в третьей степени, т.е. теоретические изотермы реальных газов (изотермы Ван-дер-Ваальса) не равнобочные гиперболы как изотермы для идеальных газов (рис. 1) и при низких температурах могут иметь два экстремума. Иными словами, уравнение (2), как уравнение третьей степени относительно V, может иметь либо три вещественных корня, либо один вещественный и два мнимых, лишенных физического смысла, корня. На рис.5 изображены изотермы Ван-дер-Ваальса для различных значений температуры и видно, что первому случаю соответствуют изотермы при низких температурах (три значения объема газа V1 , V2 и V3 отвечают одному значению давления p1), второму случаю – изотермы при высоких температурах. При некоторой температуре Тк на изотерме имеется лишь одна точка перегиба К (критическая - точка перегиба или критическая точка), которая соответствует критическому состоянию системы со своими критическими параметрами pк, Vк, Tк.
При температурах T< Tк изотермы Ван-дер-Ваальса имеют волнообразный участок и три корня.
В природе переходы из состояния 3→4→5 не осуществляются (рис. 6) (при сжатии вещества давление увеличивается), поэтому истинная изотерма − это линия, проходящая через точки 1-2-4-6-7. Экспериментально такая линия (изотерма для реальных газов) впервые была получена Эндрюсом в 1869г. незадолго до теоретических исследований Я. Д. Ван-дер-Ваальса.
Если через крайние точки (2 и 6) горизонтальных участков семейства изотерм провести линию (рис.6), то получится колоколообразная кривая (пунктирная линия на рис. 7), которая с критической изотермой Tk (с изотермой проходящей через критическую точку) все поле (p,Vm) делит на 4 области, где вещество может находиться; в состояние жидкости (Ж), жидкости и насыщенного пара (двухфазное состояние), (Ж+П), Пара и Газа.
Правда, при некоторых условиях могут быть реализованы состояния (метастабильные или неустойчивые), соответствующими участкам 5−6 и 2−3 (рис. 9). Такие фазы ограниченно устойчивы. Надо отметить, что существуют и другие уравнения, описывающие (иногда даже более точно) состояние реальных газов, но они более сложны.
Основы термодинамики. Первое начало термодинамики Основы термодинамики составляют первое начало термодинамики, которое описывает количественную и качественную стороны процессов превращения энергии тепловых (беспорядочных) движении молекул, и второе начало термодинамики, которое позволяет судить о направлении этих процессов. Внутренняя энергия термодинамической системы – это энергия хаотического (теплового) движения микрочастиц системы (молекул, атомов, электронов, ядер и т.д.) и энергия взаимодействия этих частиц. Сюда не относится ни кинетическая энергия движения системы как целого, ни потенциальная энергия системы во внешних полях. Для идеальных газов, по определению, энергия взаимодействия микрочастиц не учитывается. Внутренняя энергия – однозначная функция термодинамического состояния системы и при переходе системы из одного термодинамического состояния в другое, изменение внутренней энергии определяется только разностью значений внутренней энергии этих состояний и не зависит от пути перехода. Первое начало термодинамики отражает закон сохранения энергии для термодинамических систем, где существуют две формы передачи энергии – работа и теплота: т.е. внутренняя энергия системы может изменяться в результате совершения над системой работы (двигая поршень, изменяем температуру) или в результате сообщения ей теплоты (энергии, переданной системе внешними телами путем теплообмена). Допустим, что некоторая система (газ под поршнем), обладая внутренней энергией U1, получила некоторое количество теплоты Q и, переходя в новое состояние, характеризующееся внутренней энергией U2, совершила работу A над внешней средой, т.е. против внешних сил. Количество теплоты считается положительным, когда оно подводится к системе, а работа – положительной, когда система совершает ее против внешних сил. Многовековый опыт показывает, что изменение внутренней энергии: ΔU=U2 – U1 =Q-A или Q= ΔU+A или в более корректной, дифференциальной форме δQ=dU+δA, где dU − бесконечно малое изменение внутренней энергии системы (полный дифференциал), δA − элементарная работа (частный дифференциал), δQ − бесконечно малое количество теплоты (частный дифференциал).
Теплота, переданная системе, идет (расходуется) на изменение внутренней энергии системы и на совершаемую системой работу против внешних сил (первое начало термодинамики). Первое начало термодинамики как обобщение закона сохранения и превращения энергии утверждает: будучи несоздаваемой и неуничтожимой, энергия может видоизменяться. Если система периодически возвращается в исходное состояние, то ΔU=0, тогда согласно первому началу термодинамики A=Q.
Т.е. вечный двигатель первого рода – периодически действующий двигатель, который совершил бы большую работу, чем сообщенная ему извне энергия (теплота) – невозможен. Это тоже одна из формулировок первого начала термодинамики.
Работа газа при изменении его объема
Полная работа A, совершаемая газом при расширении от объема V1 до объема V2, определяется площадью A между кривыми p=f(V), p=0, V=V1, V=V2. Это справедливо при любых изменениях V твердых, жидких и газообразных тел. Графически можно изображать только равновесные процессы – процессы, состоящие из последовательности равновесных состояний. Они протекают так, что изменение термодинамических параметров за конечный промежуток времени бесконечно мало. Все реальные процессы неравновесны (они протекают с конечной скоростью), но в ряде случаев неравновесностью реальных процессов можно пренебречь (чем медленнее процесс протекает, тем ближе он к равновесному). В дальнейшем рассматриваемые процессы будем считать равновесными
Теплоемкость
Удельная теплоемкость вещества c − Это количество теплоты δQ, необходимое для нагревания 1кг вещества на 1 градус Кельвина.
Молярная теплоемкость Cm − Количество теплоты δQ, необходимое для нагревания 1 моль вещества на 1 градус Кельвина.
где n=m/M − количество вещества, а М – молярная масса вещества. Cm=c∙M Различают теплоемкость при постоянном объеме − CV, и при постоянном давлении − Cp. Из первого начала термодинамики имеем δQ=dU+δA. Используя δA=pdV Cm=δQ/(ndT), для 1 моль газа получаем CmdT=dUm+pdVm Если V=const,δA=0, то
т.е. молярная теплоемкость газа при постоянном объеме CV равна изменению внутренней энергии 1 моль газа при повышении его температуры на 1К. При p=const, из CmdT=dUm+pdVm получим Т.к. Cp=CV+R (Уравнение Майера) Всегда Cp > CV т.к. нагревание при p=const требует дополнительное количество теплоты для расширения газа, т.к. p=const обеспечивается увеличением V. Из CV=iR/2 → Параметр коэффициент Пуассона (подробнее см. приложение 5). Видно, что Cp и CV не зависят от Т и определяются лишь числом свободы. Но это справедливо только у одноатомного газа. Уже у двухатомных газов i=i(T). Например, у водорода при комнатной температуре по теории i=iпоступ+iвращ+2iколеб=3+2+2 Между тем эксперимент дает; при низких температурах T≈50K, CV=(3/2)R, при комнатных − T≈300K, CV=(5/2)R (вместе теоретических (7 /2)R), при очень высоких − T≈6000K, CV=(7/2)R.
При низких Т наблюдаются только поступательное движение молекул (i=3), а энергии теплового движения недостаточно, чтобы «включить» вращательные или колебательные движения, для которых необходимы определенные «квантованные» энергии. Поэтому соответствующая степень свободы «замораживается» – к ней неприменим закон равнораспределения энергии. При комнатных температурах к поступательным движениям добавляются вращение молекул и i=5, а при высоких, к этим двум видам движения добавляются еще колебания молекул и i=7. Второе начало термодинамики I начало термодинамики не указывает направление протекания термодинамических процессов. Можно представить множество процессов, не противоречащих первому началу, в которых энергия сохраняется, но в природе они не осуществляются. Чтобы определить направление протекания термодинамических процессов и ответить на вопрос, какие процессы в природе возможны, а какие нет, вводится понятие энтропии (S) как функции состояния термодинамической системы. Для определения энтропии рассматривают приведенное количество теплоты Термодинамический процесс обратимый, если он может происходить как в прямом, так и в обратном направлении. Любой равновесный процесс является обратимым, но реальные процессы − необратимые. Обратимый процесс − это идеализация реальных процессов (физическая модель). Строгий термодинамический анализ показывает, что в любом обратимом круговом процессе
Т. к. если интеграл по замкнутому контуру равняется нулю, то подынтегральное выражение есть полный дифференциал некоторой функции, которая определяется только состоянием системы и не зависит от пути, пройденного системой. Эта функция состояния, дифференциал которой является δQ/T, называется энтропией и обозначается S (термин энтропия, от греч. слов «эн» – в, «тропе» – превращение – обращенная внутрь, недоступная для дальнейших превращений, ввел Клаузиус 1865г.). Таким образом,
Из формулы (3) вытекает, что для обратимых процессов ΔS=0. В термодинамике доказывается, что энтропия замкнутой системы, совершающей необратимый цикл, возрастает: ΔS>0. Таким образом, энтропия замкнутой системы может либо возрастать (в случае необратимых процессов), либо оставаться постоянной (в случае обратимых процессов): ΔS≥0 (неравенство Клаузиуса). Так как реальные процессы необратимы, то все процессы в замкнутой системе ведут к увеличению ее энтропии [ Второе начало термодинамики (принципа возрастания энтропии)]. Энтропия может рассматриваться как мера вероятности состояния термодинамической системы. Все естественные процессы в изолированной термодинамической системе протекают так, что система переходит от состояний менее вероятных к состояниям более вероятным (которые являются также более беспорядочными). Это иное определение в торого начала термодинамики.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 595; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.201.114 (0.017 с.) |

 Соотношение, связывающие между собой параметры состояния газа, называется уравнением состояния газа.
Соотношение, связывающие между собой параметры состояния газа, называется уравнением состояния газа.
 Используя законы Бойля – Мариотта и Гей-Люссака, Клапейрон вывел уравнение состояния идеального газа для любых термодинамических процессов. Выведем уравнения Клапейрона при помощи изотермических и изохорных процессов (рис.3).
Используя законы Бойля – Мариотта и Гей-Люссака, Клапейрон вывел уравнение состояния идеального газа для любых термодинамических процессов. Выведем уравнения Клапейрона при помощи изотермических и изохорных процессов (рис.3). .
. ,
, =nRT, (2)
=nRT, (2) .
. Эти силы межмолекулярного взаимодействия
Эти силы межмолекулярного взаимодействия  , где для сил притяжения n=7, а для сил отталкивания n=9
, где для сил притяжения n=7, а для сил отталкивания n=9  15. Например, на расстоянии r~10−9м силы притяжения fпр(r)~−1/r7, на расстоянии r~10−10м, fот(r)~1/r13.
15. Например, на расстоянии r~10−9м силы притяжения fпр(r)~−1/r7, на расстоянии r~10−10м, fот(r)~1/r13. молекул (
молекул ( Учитывая собственный объем молекул и силы межмолекулярного взаимодействия, Я. Д. Ван-дер-Ваальс (1873г.) в уравнении Клапейрона − Менделеева (pVm=RT) ввел две поправки и вывел уравнение состояния реального газа:
Учитывая собственный объем молекул и силы межмолекулярного взаимодействия, Я. Д. Ван-дер-Ваальс (1873г.) в уравнении Клапейрона − Менделеева (pVm=RT) ввел две поправки и вывел уравнение состояния реального газа: или
или 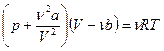 ,
,

 Пар отличается от остальных газообразных состояний тем, что при изотермическом сжатии претерпевает процесс сжижения (т. е. переход от газа к жидкости) (кривая 1 на рис.8). Газ же при Т > Тк не может быть превращен в жидкость ни при каком давлении (кривая 2).
Пар отличается от остальных газообразных состояний тем, что при изотермическом сжатии претерпевает процесс сжижения (т. е. переход от газа к жидкости) (кривая 1 на рис.8). Газ же при Т > Тк не может быть превращен в жидкость ни при каком давлении (кривая 2).
 dA=F∙dℓ=pSdℓ=pV
dA=F∙dℓ=pSdℓ=pV
 [ Дж/(кг∙К) ]
[ Дж/(кг∙К) ]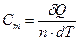 [ Дж/(моль∙К) ],
[ Дж/(моль∙К) ], . Используя
. Используя  , получим
, получим


 − показатель адиабата или
− показатель адиабата или 1=7, а
1=7, а  .
.
 как отношение теплоты Q, полученной телом в изотермическом процессе, к температуре T теплоотдающего тела.
как отношение теплоты Q, полученной телом в изотермическом процессе, к температуре T теплоотдающего тела. . (3)
. (3) .
.


