
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Энтопия. Общие формулы для энтропии идеального а реального газов.Содержание книги
Поиск на нашем сайте
Энтропия на опыте не определяется, поэтому нужно получить формулы, позволяющие вычислить её значение. Энтропиею называют «тенью энергии», и она, как U, является функцией состояния, т.е. dS – полный дифференциал. Любую из функций состояния можно выразить через любое сочетание термодеформационных параметров состояния, например для термодеформационной системы энтропия может быть выражена через любые сочетания: S=S(T,v); S=S(T,v); S=S(P,v) Получим первую группу функций для вычисления энтропии, полагая, что энтропия выражается через сочетание S=S(T,v). I. S = S(T,v), по правилам математики полного дифференциала функции двух переменных можно для нашего случая записать:
Частная производная
Окончательно получим формулу для вычисления энтропии любого газа (реального и идеального) в любом процессе:
Как частный случай рассмотрим идеальный газ:
Найдем неопределенный интеграл формулы (89):
Пусть
где Рассмотрим адиабатный обратимый процесс(S=const). Проанализируем формулу (90), так как левая часть должна равняться правой части, а
(91)- уравнение адиабаты идеального газа, одно из трех уравнений Пуассона. Для практики наибольший интерес представляет не абсолютное значение S, а её изменение dS.
а) Пусть
из неё можно получить частные зависимости:
Энтропия – мера неупорядоченности системы. По 3-ему закону термодинамики (следствие тепловой теоремы Нернста) абсолютный ноль температур не достижим, поэтому при T®0 и S®0, но не будет равняться нулю.На практике нулевое значение энтропии может быть задано произвольно. Условились за начало отсчёта энтропии принимать 0,1°С. Тогда, полагая, что при нормальных условиях S=0 (Рн=101325Па, Tн=273,15 K). Примечание: в инженерной практике, начало отсчета внутренней энергии U и энтальпии также полагается нормальные физические условия. Удельный объем при НФУ из уравнения Менделеева-Клапейрона(pv=RT) определяется по этой формуле:
Если в формуле (92) вместо Т1 и v1 взять их значение при НФУ и опустить индексы, как ненужные, то получим формулу:
Примечание: По закону Авогадро один Кмоль любого газа при одинаковых условиях занимает один и тот же объём, при нормальных физических условиях 1 Кмоль любого газа занимает объём равный 22,4 м3. Во всех вышеприведённых формулах cv – массовая изохорная теплоёмкость – бралась средним значением. Получим формулы для случая линейной зависимости теплоёмкости от температуры, т.е. cv=c0v+aT подставим
Принимая за начало отсчёта S нормальные физические условия, получим формулы для расчёта энтропии:
Получим вторую группу формул для расчёта энтропии: II. S = S(T,p), алгоритм вывода аналогичен группе 1
(99)- изменение энтропии любого газа (идеального и реального) в любом процессе). Частный случай. Рассмотрим идеальный газ:
Найдем неопределенный интеграл из формулы (100):
Пусть
Рассмотрим адиабатный обратимый процесс(S=const). При выполнении равенства требуется чтобы:
Одно из трех уравнений Пуассона. Вернемся к формуле (100) и возьмем определенный интеграл, и получим:
Из формулы следует два частных случая:
Если взять за начало отсчёта S нормальные физические условия, получим формулу:
Следует два частных случая:
Для случая линейной зависимости теплоемкости от температуры получим зависимости:
Отсчитывая энтропию от НФУ получим:
Получим третью группу формул: III. S = S(p,v), алгоритм вывода аналогичен первому и второму.
(109)- справедлива для любого газа в любом процессе. Рассмотрим идеальный газ (уравнение не упрощается):
После подстановки получим:
Окончательно:
Найдем неопределенный интеграл формулы (110):
Пусть
, где k – показатель адиабаты. Рассмотрим адиабатный обратимый процесс (S=const, dQ=0):
(111)- уравнение адиабаты идеального газа, или уравнение Пуассона. Таким образом, имеем три уравнения Пуассона:
Возьмём определённый интеграл формулы (110):
Полагая за начало отсчёта S нормальные физические условия, получим формулу:
где Частные случаи: p=const: v=const: Вышеприведённые формулы получены в предположении постоянства теплоёмкости. Получим формулы для случая линейной зависимости теплоёмкости: 1) cv=c0v+aT, cp=c0p+aT, где c0v, a, c0p – постоянные.
Найдём значение
Найдем определенный интеграл формулы (114):
Частные случаи:
Преобразуя формулу (118) получим:
Окончательно:
Полагая, что S=0 при нормальных физических условиях, получим:
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 577; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.218.134 (0.005 с.) |

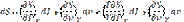 , ранее была получена формула (77)
, ранее была получена формула (77)  , с ее учетом получим:
, с ее учетом получим: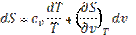
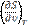 относится к третьему типу
относится к третьему типу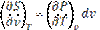
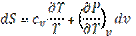 (88)
(88)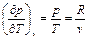
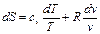 (89)
(89) .
.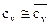 - среднее значение массовой изохорной теплоёмкости, тогда
- среднее значение массовой изохорной теплоёмкости, тогда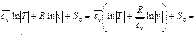
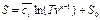 (90)
(90)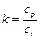 .
.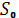 ,
, 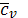 являются const, то выполняется условие:
являются const, то выполняется условие: (91)
(91)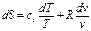 (*) – возьмём определённый интеграл:
(*) – возьмём определённый интеграл: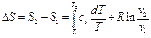
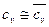 получим:
получим: (92)
(92) (93)
(93)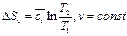 (94)
(94)

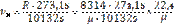
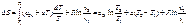 (95) тогда
(95) тогда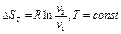 ;
; 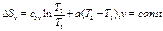 .
.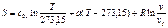 ,
,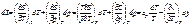
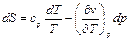 (99)
(99)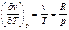
 (100)
(100)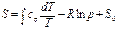 .
.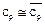
 - среднее значение массовой изобарной теплоёмкости, тогда:
- среднее значение массовой изобарной теплоёмкости, тогда: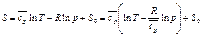 , здесь:
, здесь: 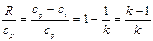
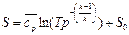 .
. (101)
(101)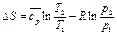 (102)
(102)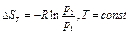 (103)
(103)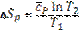 ,
, 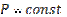 (104)
(104)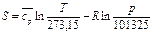 (105)
(105)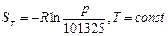 (106)
(106)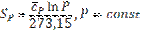 (107)
(107)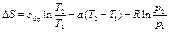 ,
,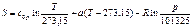 (108)
(108)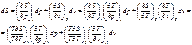
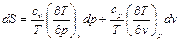 (109)
(109)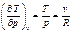 ,
, 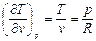 (66)
(66)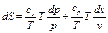 ;
;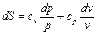 (110)
(110)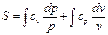 +S0
+S0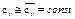 ;
; 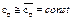
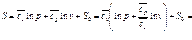
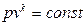 (111)
(111)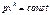 ;
; ;
; .
.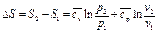 (112)
(112) (113)
(113)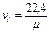
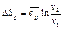 ,
, 
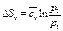 ,
, 
 =?:
=?: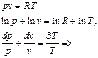
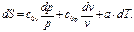 (114)
(114)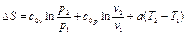 (115)
(115) (116)
(116)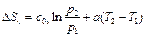 (117)
(117)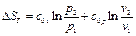 (118)
(118)
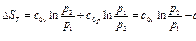

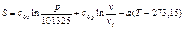 (119)
(119)


