
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Особенности термодинамики как науки.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Особенности термодинамики как науки.
Термодинамика – наука о свойствах энергии в различных её видах и закономерностях перехода её от тела к телу, из вида в вид. Термодинамика подразделяется на: 1) физическую термодинамику (общую); 2) техническую термодинамику; 3) химическую термодинамику; 4) термодинамику электрических и магнитных явлений и т.д. Также существует деление термодинамики на: 1) равновесную (классическую); 2) неравновесную (находится в стадии развития). Термодинамика – наука дедуктивная, позволяет получить наиболее общие закономерности, которые могут быть применены к конкретным частным случаям. Термодинамика – наука макроскопическая. Она не рассматривает процессы на уровне микрочастиц. В этом заключается её сила и слабость. Термодинамике чужды представления о модельном строении вещества. Все кардинальные изменения в представлениях о строении вещества не сказываются на основных результатах термодинамики (это её сила), а слабость – в том, что термодинамика не может получить некоторые требуемые соотношения и вынуждена заимствовать эти результаты у других наук, например, обращаться к теоретической или экспериментальной физике. Термодинамика феноменологична, т.е. некоторые положения в термодинамике не имеют должного теоретического основания и берутся лишь на основании многочисленных опытов и экспериментов. Термодинамика базируется на понятии макроскопического равновесия, т.е. рассматривают состояния систем тогда, когда все термодинамические процессы находятся в равновесном состоянии. Макроскопическое равновесие не означает прекращение взаимодействия на уровне микрочастиц. Основные определения термодинамики.
Система – тело или совокупность тел, являющихся объектом изучения. Пр.: Если изучается газ, то системой является газ, всё остальное (сосуд, поршень и т.п.) – окружающая среда. Процесс – изменение физических параметров системы, сопровождающиеся изменением термодинамических параметров системы. Координаты и потенциалы. Координатами состояния системы называются величины, которые изменяются при наличии данного взаимодействия и остаются неизменными при его отсутствии, т.о. координаты состояния системы – это индикаторы наличия данного взаимодействия. Изменение величины, вызываемой координатой, свидетельствует о наличии процесса. xk – обозначение координаты состояния при k-том взаимодействии. Пример 1. Деформационное (механическое), взаимодействие. Это взаимодействие всегда сопровождается изменением объема системы W, м3. В инженерных расчетах часто используется удельный объем V,
т.о. при деформационном (механическом) взаимодействии координатой состояния взаимодействия является удельный объем V. W – м3, v, Xдеф является удельный объём v. Пример 2. Тепловое взаимодействие. При тепловом взаимодействии всегда имеет место обмен между системой и окружающей средой. В ходе развития науки было установлено, что координаты состояния системы является величина называемая энтропией. Удельной энтропией системы Энтропия как термодинамический параметр системы опытным путем не определяется и определяется только опытным путём. Приборов для ее измерения нет. Значения энтропии определяются только расчетным путем по специальным методикам. Пример 3. Химические реакции и фазовые превращения. В этом случае координатой состояния системы является mi – масса i-тых компонентов системы. У каждого взаимодействия данного рода есть только одна координата состояния системы. Xх\ф является mреагентов или фазовых системы , т.е. меняется масса. Потенциал – физическая величина, разность которой у системы и окружающей среды вызывает процесс. Обозначается Pk потенциал при k-том взаимодействии. P kl– потенциал окружающей среды при k-том взаимодействии; P ki – потенциал системы при k-том взаимодействии.
Правило знаков для потенциалов: Разность потенциалов между окружающей средой и системой считается положительной, если соответствующая координата состояния системы при этом возрастает, и наоборот отрицательной, если соответствующая координата состояния системы при этом убывает.
Рассмотрим в качестве примера деформационное (механическое) взаимодействие. P1- абсолютное давление окружающей среды Pi- абсолютное давление системы в данном случае газа. При P1-Pi>0 dxдиф<0 Т.о. абсолютное давление как потенциал при деформационном взаимодействии не проходит по правилу знаков, т.к. при положительной разности потенциалов объём системы (и удельный объем) убывает, а не возрастает, а не возрастает как это требует правило знаков. Для выполнения правила знаков следует взять абсолютное давление со знаком «-». Во всех формулах термодинамики используется только абсолютное давление измеряемое в Па (Н/м2) Pдеф – (-p) p – абсолютное давление (Па). Манометры показывают превышение давления в системе над атмосферным, поэтому показания манометров показывают избыточное давление, при котором абсолютное находится как p = pман + pбарометрическое. Если в системе имеется разрежение (вакуум), то абсолютное давление P = B – pвак, где B – барометрическое давление, pвак – показания вакуумметра.
Тепловое взаимодействие. Pтепл – T, [K] T – абсолютная термодинамическая температура. T = t°C + 273,15 t°F = Наиболее близки к абсолютной температуре показатели газовых термометров. В ходе развития науки было установлено, что потенциалом при химических и фазовых взаимодействиях (Pх\ф) является величина химического термодинамического потенциала (μ).
Характеристические функции.
Все характеристические функции являются функциями состояния. Функция называется характеристической, если её частная производная по некоторому параметру даёт другой параметр, а именно, соответствующий тому, по которому производится дифференцирование. 1. Рассмотрим сопряжение по координатам: В этом случае, в качестве независимо изменяющихся параметров выступают только координаты, а потенциалы отслеживают их изменение по каким-либо зависимостям. Как было показано ранее, внутренняя энергия является функцией состояния и полностью определяется всей совокупностью координат состояния системы. U=U(X1, X2,…, Xn) (17) Дифференциалы всех функций состояния являются полными дифференциалами, поэтому dU- полный дифференциал. В соответствии с правилами математики нахождение полного дифференциала функции нескольких переменных
Xinv – означает, что все остальные координаты инвариантны, т.е. не являются переменными (замороженными).
Из первого начала термодинамики в общем виде (3) и формулы (23) следует равенство правых частей.
Так как данное равенство должно выполняться при любом k, то получаем
Из сравнения полученного выражения формулы (24) и определения характеристической функции следует вывод о том, что внутренняя энергия является характеристической функцией при сопряжении по координатам. Введем общее обозначение характеристической функции Y(пси). Y(Xk)=U (25) Дифференциалом этой характеристической функции является первое начало термодинамики в общем виде. В качестве примера рассмотрим термодеформационную систему.
Y(S,v)=U
Из первого начала термодинамики получается
dU=TdS–pdv (28) (28)- первое начало термодинамики в обычной форме для термодеформационной системы. В общем случае (для любой системы) при сопряжении по координатам дифференциальной характеристикой функции определяется по формуле:
dU=dY
2. Рассмотрим сопряжение по потенциалам: При этом виде сопряжения независимым образом изменяются только потенциалы, а координаты отслуживают их изменение по каким-либо конкретным формулам, так как изменяются зависимым образом. Вывод аналогичен случаю 1, можно сразу записать итоговую формулу: 1) 2) 3) Рассмотрим в качестве примера термодеформационную систему:
Из (29) =>Y(T,p) = U – TS + pv – эта характеристическая функция в термодинамике имеет обозначение и название F=U–TS+pv (32) (32)– свободная энтальпия (удельная свободная энтальпия); Из(30)=>dF=SdT+vdp (33) По своей сути уравнение (33) это одна из форм первого начала термодинамики. Из(31)=>
Свободная энтальпия – часть энтальпии (i), которая может быть использована в каких-либо технических целях. Энтальпию раньше называли теплосодержанием.
3) Смешанное сопряжение. В этом случае в качестве независимых параметров выступают не все n потенциалов, а только r потенциалов от общего числа. Такие независимые потенциалы будем обозначать: Pi, i=1,2,3,…,r., r <n Независимые координаты обозначим как j=(r+1),(r+2),…,n Опуская вывод (аналогичен случаю 1), сразу запишем окончательное выражение.
Рассмотрим термодеформационную систему
1) Пусть независимым образом изменяется потенциал – Т и независимая координата – v: Тогда из (36) =>Y(T,v) = U – TS Эта характеристическая функция имеет свое обозначение и название. F=U-TS (40) Уравнение (40) это свободная энергия В химической термодинамике F называется изохорно-изотермическим потенциалом. В соответствие с формулой (37) дифференциал этой функции: dF = – S dT – p dv (41) По физической сути это одна из форм первого начала термодинамики. Из формул (38), (39) следует:
Если рассмотреть в формуле (41) изотермический процесс, где T=const, то dFT = – p dv (44) так как dA = p dv, то в соответствии с формулой (44) в изотермических процессах абсолютная работа, совершаемая системой, производится за счёт убыли свободной энергии ∆FT=-AT или: AT= -∆FT (45) Ранее отмечалось, что в изотермических процессах вся подведённая к системе теплота идёт на совершение абсолютной работы. 2) Независимым потенциалом является абсолютной давление (P), а независимой координатой энтропия (S). В соответствии с формулами (36-39) можно записать Y(p,S) = U + pv, эта характеристическая функция называется энтальпией i. i=U+pv[ (46)
По физическому смыслу произведение p на v это потенциальная энергия одного килограмма газа при давлении p и удельного объема v.
S- Площадь поршня M- Масса груза P- Давление в системе (газа под поршнем) W-Объем системы (газа под поршнем) H- Высота поднятия поршня
Eпот = pSH = pW. Если отнести Eпот к 1 кг системы, то Так как внутренняя энергия идеального газа зависит только от температуры и не учитывает давление газа, то энтальпия полнее учитывает энергетические возможности системы с точки зрения совершения работы. Di=VdP+TdS (47) Как известно, TdS=dQ, тогда уравнение примет вид:di=VdP+dQ Рассмотрим частный случай, где P=const (изобарный) Dip=dQp (48) После интегрирования получим ∆ip=i2-i1=Qp или Qp=i2-i1 (49) Из формулы (49) следует, что в изобарных процессах теплота процесса определяется как разность энтальпии, конечного и начального состояния.
Рассмотрим формулу (47) di=VdP+TdS, тогда di=VdP+dQ или dQ=di-VdP (52) Уравнение (52) это первое начало термодинамики в энтальпийной форме. Введем обозначение Aрасп. Располагаемая работа- это работа, которая может быть передана другой системе.
Рассмотрим произвольный процесс расширения системы 1-2
С учетом (53) уравнение (52) запишется как dQ=di+dAрасп (54) Формулировка первого начала термодинамики в энтальпийной форме из (54): Подведенная к системе теплота идее на изменение ее энтальпии и не совершает располагаемой работы.
Мнемонический приём для термодеформационной системы:
Вычисление энтропии. Второй закон термодинамики. 1-ый закон термодинамики говорит, что невозможно получить работу без подвода энергии, в частности в форме теплоты, из вне, т.е. закон говорит о возможности взаимопревращения работы в теплоту, но не устанавливает особенности превращения теплоты в работу или работы в теплоту. Но работа в теплоту превращается легко и просто, а для превращения теплоты в работу нужны сложные технические устройства, и процесс превращения теплоты в работу всегда сопровождается потерями. С точки зрения физики различие кроется на уровне превращения упорядоченного движения в хаотическое (A®Q) и хаотическое в упорядоченное. Все процессы в природе подразделяются на самопроизвольные и вынужденные (падение давления в сосуде при разгерметизации, диффузия газов и т.д. – самопроизвольные; нагнетание давления, разделение газов, в общем случае превращение теплоты в работу – вынужденные процессы). Ранняя формулировка 2-ого закона термодинамики (формулировка Томсона): «Невозможно провести отрицательный (вынужденный) процесс без компенсации его положительным самопроизвольным процессом». Пример: Таяние снега – вынужденный процесс – сопровождается отдачей тепла от более теплого более холодному (излучение, радиация) - самопроизвольный процесс. Формулировка: «Каждый вынужденный процесс избегает одиночества и требует сопровождения самопроизвольным процессом». Известны и другие формулировки 2-ого закона термодинамики: «Невозможно построить тепловой двигатель, КПД которого превышал бы цикл Карно»; «Вечный двигатель 2-ого рода невозможен»; «Энтропия в адиабатически изолированных системах всегда возрастает». Вечный двигатель 2-ого рода – двигатель, источником теплоты которого является теплота окружающей среды. С точки зрения 1-ого закона это возможно, но 2-ой закон утверждает, что должно быть два источника теплоты: нагреватель и холодильник. Цикл Карно:
Только для обратимых процессов: dQ = T dS, Q1 = T1(S2 – S1), Q2 = T2(S1 – S2). Для любых процессов (обратимых и необратимых) Если подставить Q1 и Q2, то получим
Теорема Карно КПД обратимого цикла Карно не зависит от состава топлива и определяется температурами нагревателя T1 и холодильника T2. Все реальные процессы необратимы, т.е.
В то время, как для обратимого:
Произвольный обратимый цикл
Разобьем цикл бесчисленным числом адиабат и образуем бесчисленное количество обратимых циклов Карно. Справедливо следующее равенство:
Из математики известно, что линейный интеграл по замкнутому контуру равен нулю В необратимых процессах dQ ¹ T dS. Рассмотрим гипотетический процесс, который состоит из обратимых и необратимых частей. Суммарно процесс является необратимым, тогда
Клаузиус рассматривал адиабатный процесс в масштабах всей Вселенной (суммарно адиабатный процесс). Он пришёл к выводу Энтропия – мера неупорядоченности системы. Sгаза>Sжидк>Sтв.тел. По Клаузиусу движение во Вселенной хаотично. Теплота от более нагретых тел к менее нагретым будет излучаться во Вселенную и передаваться другим космическим телам и через большой промежуток времени температура во Вселенной выровняется, но если температура будет одинаковой, то преобразование теплоты в работу невозможно, как следует из теоремы Карно у тепловых двигателей должно быть два источника теплоты (нагреватель и холодильник). Но если температура во Вселенной будет постноянной, то преобразование теплоты в работу станет невозможным. Это состояние называется тепловой смертью Вселенной. Критика тепловой смерти Вселенной. Если будет конец, значит было начало, а в масштабах бесконечного вселенского времени таких начал и концов должно быть также бесконечное множество. Отсюда согласуется гипотеза пульсирующей Вселенной. С точки зрения статистической физики критику тепловой смерти дал Гольцман. Согласно ему: «Термодинамическое состояние системы – это её наиболее вероятное состояние (флуктуация)», поэтому dS>0 - наиболее вероятный вариант развития Вселенной, но наряду с тем есть процессы флуктуации, когда dS<0, последннее компенсирует первое.
(Природа Вселенной не ясна, поэтому считать её адиабатической не стоит). Третий закон термодинамики (следствие тепловой теоремы Нернста): По теореме T®0 S®0, абсолютный нуль по шкале Кельвина невозможен.
Особенности термодинамики как науки.
Термодинамика – наука о свойствах энергии в различных её видах и закономерностях перехода её от тела к телу, из вида в вид. Термодинамика подразделяется на: 1) физическую термодинамику (общую); 2) техническую термодинамику; 3) химическую термодинамику; 4) термодинамику электрических и магнитных явлений и т.д. Также существует деление термодинамики на: 1) равновесную (классическую); 2) неравновесную (находится в стадии развития). Термодинамика – наука дедуктивная, позволяет получить наиболее общие закономерности, которые могут быть применены к конкретным частным случаям. Термодинамика – наука макроскопическая. Она не рассматривает процессы на уровне микрочастиц. В этом заключается её сила и слабость. Термодинамике чужды представления о модельном строении вещества. Все кардинальные изменения в представлениях о строении вещества не сказываются на основных результатах термодинамики (это её сила), а слабость – в том, что термодинамика не может получить некоторые требуемые соотношения и вынуждена заимствовать эти результаты у других наук, например, обращаться к теоретической или экспериментальной физике. Термодинамика феноменологична, т.е. некоторые положения в термодинамике не имеют должного теоретического основания и берутся лишь на основании многочисленных опытов и экспериментов. Термодинамика базируется на понятии макроскопического равновесия, т.е. рассматривают состояния систем тогда, когда все термодинамические процессы находятся в равновесном состоянии. Макроскопическое равновесие не означает прекращение взаимодействия на уровне микрочастиц. Основные определения термодинамики.
Система – тело или совокупность тел, являющихся объектом изучения. Пр.: Если изучается газ, то системой является газ, всё остальное (сосуд, поршень и т.п.) – окружающая среда. Процесс – изменение физических параметров системы, сопровождающиеся изменением термодинамических параметров системы. Координаты и потенциалы. Координатами состояния системы называются величины, которые изменяются при наличии данного взаимодействия и остаются неизменными при его отсутствии, т.о. координаты состояния системы – это индикаторы наличия данного взаимодействия. Изменение величины, вызываемой координатой, свидетельствует о наличии процесса. xk – обозначение координаты состояния при k-том взаимодействии. Пример 1. Деформационное (механическое), взаимодействие. Это взаимодействие всегда сопровождается изменением объема системы W, м3. В инженерных расчетах часто используется удельный объем V,
т.о. при деформационном (механическом) взаимодействии координатой состояния взаимодействия является удельный объем V. W – м3, v, Xдеф является удельный объём v. Пример 2. Тепловое взаимодействие. При тепловом взаимодействии всегда имеет место обмен между системой и окружающей средой. В ходе развития науки было установлено, что координаты состояния системы является величина называемая энтропией. Удельной энтропией системы Энтропия как термодинамический параметр системы опытным путем не определяется и определяется только опытным путём. Приборов для ее измерения нет. Значения энтропии определяются только расчетным путем по специальным методикам. Пример 3. Химические реакции и фазовые превращения. В этом случае координатой состояния системы является mi – масса i-тых компонентов системы. У каждого взаимодействия данного рода есть только одна координата состояния системы. Xх\ф является mреагентов или фазовых системы , т.е. меняется масса. Потенциал – физическая величина, разность которой у системы и окружающей среды вызывает процесс. Обозначается Pk потенциал при k-том взаимодействии. P kl– потенциал окружающей среды при k-том взаимодействии; P ki – потенциал системы при k-том взаимодействии.
Правило знаков для потенциалов: Разность потенциалов между окружающей средой и системой считается положительной, если соответствующая координата состояния системы при этом возрастает, и наоборот отрицательной, если соответствующая координата состояния системы при этом убывает.
Рассмотрим в качестве примера деформационное (механическое) взаимодействие. P1- абсолютное давление окружающей среды Pi- абсолютное давление системы в данном случае газа. При P1-Pi>0 dxдиф<0 Т.о. абсолютное давление как потенциал при деформационном взаимодействии не проходит по правилу знаков, т.к. при положительной разности потенциалов объём системы (и удельный объем) убывает, а не возрастает, а не возрастает как это требует правило знаков. Для выполнения правила знаков следует взять абсолютное давление со знаком «-». Во всех формулах термодинамики используется только абсолютное давление измеряемое в Па (Н/м2) Pдеф – (-p) p – абсолютное давление (Па). Манометры показывают превышение давления в системе над атмосферным, поэтому показания манометров показывают избыточное давление, при котором абсолютное находится как p = pман + pбарометрическое. Если в системе имеется разрежение (вакуум), то абсолютное давление P = B – pвак, где B – барометрическое давление, pвак – показания вакуумметра.
Тепловое взаимодействие. Pтепл – T, [K] T – абсолютная термодинамическая температура. T = t°C + 273,15 t°F = Наиболее близки к абсолютной температуре показатели газовых термометров. В ходе развития науки было установлено, что потенциалом при химических и фазовых взаимодействиях (Pх\ф) является величина химического термодинамического потенциала (μ).
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 788; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.73.221 (0.012 с.) |


 , m – масса системы, кг.
, m – масса системы, кг. - удельный объём
- удельный объём называется отношение энтропии к ее массе.
называется отношение энтропии к ее массе. , если dxk > 0
, если dxk > 0 , если dxk < 0
, если dxk < 0 t°C + 32
t°C + 32

 (23)
(23) =
= 
 (24)
(24) (26)
(26) (27)
(27) )=
)= 
 (29)
(29) (30)
(30) (31)
(31) (34)
(34) (35)
(35)
 (36)
(36) (37)
(37) (38)
(38)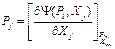 (39)
(39) (42)
(42) (43)
(43)

 (50)
(50) (51)
(51) (53)
(53)




 , и т.д.
, и т.д.

 .
.


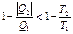 ,
,  .
.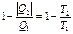 ,
,  .
.
 =>
=> 
 , где dS – полный дифференциал, т.е. её изменение не зависит от пути перехода, а только от начального и конечного состояния.
, где dS – полный дифференциал, т.е. её изменение не зависит от пути перехода, а только от начального и конечного состояния. , после интегрирования
, после интегрирования


 , т.е. по Клаузиузсу должна наступить смерть Вселенной.
, т.е. по Клаузиузсу должна наступить смерть Вселенной. .
.


