
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перечень начал термодинамикиСодержание книги Поиск на нашем сайте Начала термодинамики. Начала термодинамики — совокупность постулатов, лежащих в основе термодинамики. Эти положения были установлены в результате научных исследований и были доказаны экспериментально. В качестве постулатов они принимаются для того, чтобы термодинамику можно было построить аксиоматически. Необходимость начал термодинамики связана с тем, что термодинамика описывает макроскопические параметры систем без конкретных предположений относительно их микроскопического устройства. Вопросами внутреннего устройства занимается статистическая физика. Начала термодинамики независимы, то есть ни одно из них не может быть выведено из других начал. Перечень начал термодинамики
Работа расширения газа и внутренняя энергия. При расширении идеального газа совершается работа, которая вычисляется по уравнению:
В дифференциальной форме:
Это максимальная работа, которую совершает газ в обратимых процессах (в равновесных условиях). В необратимых процессах работа меньше, чем ее значение, вычисленное по формуле. Теплоемкость. Теплоёмкость тела (обычно обозначается латинской буквой C) — физическая величина, определяемая отношением бесконечно малого количества теплоты δ(дельта) Q, полученного телом, к соответствующему приращению его температуры δ T [1]:
Единица измерения теплоёмкости в Международной системе единиц (СИ) — Дж/
Молярная теплоемкость — теплоемкость 1 моля данного вещества. Единицы измерения — Дж/(моль К). Если же говорить про теплоемкость произвольной системы, то ее уместно формулировать в терминах термодинамических потенциалов — теплоемкость есть производная термодинамического потенциала Q по температуре: Понятие теплоёмкости определено как для веществ в различных агрегатных состояниях (твёрдых тел, жидкостей, газов), так и для ансамблей частиц и квазичастиц (в физике металлов, например, говорят о теплоемкости электронного газа). Если речь идёт не о каком-либо теле, а о некотором веществе как таковом, то различают удельную теплоёмкость — теплоёмкость единицы массы этого вещества и молярную — теплоёмкость одного моля его. Процессы в идеальном газе. Изохорический процесс. Изохорический или изохорный процесс — термодинамический процесс, который происходит при постоянном объёме. Для осуществления изохорного процесса в газе или жидкости достаточно нагревать (охлаждать) вещество в сосуде, который не изменяет своего объёма. При изохорическом процессе давление идеального газа прямо пропорционально его температуре (см. Закон Шарля). В реальных газах закон Шарля не выполняется. Термодинамика процесса Из определения работы следует, что изменение работы при изохорном процессе равно:
Чтобы определить полную работу процесса проинтегрируем данное выражение. Поскольку объем неизменен, то:
Но такой интеграл равен нулю. Итак, при изохорном процессе газ работы не совершает:
Графически доказать это намного проще. С математической точки зрения, работа процесса — это площадь под графиком. Но график изохорного процесса является перпендикуляром к оси абсцисс. Таким образом, площадь под ним равна нулю. Изменение внутренней энергии идеального газа можно найти по формуле:
где i — число степеней свободы, которое зависит от количества атомов в молекуле (3 для одноатомной (например, неон), 5 для двухатомной (например, кислород) и 6 для трёхатомной и более (например, молекула водяного пара)). Из определения и формулы теплоёмкости и, формулу для внутренней энергии можно переписать в виде:
где Используя первое начало термодинамики можно найти количество теплоты при изохорном процессе:
Но при изохорном процессе газ не выполняет работу. То есть, имеет место равенство:
то есть вся теплота, которую получает газ идёт на изменение его внутренней энергии. Теплоёмкость Молярная теплоёмкость при постоянном давлении обозначается как Молекулярно-кинетическая теория позволяет вычислить приблизительные значения молярной теплоёмкости для различных газов через значение универсальной газовой постоянной:
Теплоёмкости можно также определить исходя из уравнения Майера, если известен показатель адиабаты, который можно измерить экспериментально (например, с помощью измерения скорости звука в газе или используя метод Клемана — Дезорма). Изменение энтропии Изменение энтропии при квазистатическом изобарном процессе равно
Распределение Максвелла Распределение Ма́ксвелла — распределение вероятности, встречающееся в физике и химии. Оно лежит в основании кинетической теории газов, которая объясняет многие фундаментальные свойства газов, включая давление и диффузию. Распределение Максвелла также применимо для электронных процессов переноса и других явлений. Распределение Максвелла применимо к множеству свойств индивидуальных молекул в газе. О нём обычно думают как о распределении энергий молекул в газе, но оно может также применяться к распределению скоростей, импульсов, и модуля импульсов молекул. Также оно может быть выражено как дискретное распределение по множеству дискретных уровней энергии, или как непрерывное распределение по некоторому континууму энергии. Распределение Максвелла может и должно быть получено при помощи статистической механики (см. происхождение статсуммы). Как распределение энергии, оно соответствует самому вероятному распределению энергии, в столкновительно-доминируемой системе, состоящей из большого количества невзаимодействующих частиц, в которой квантовые эффекты являются незначительными. Так как взаимодействие между молекулами в газе является обычно весьма небольшим, распределение Максвелла даёт довольно хорошее приближение ситуации, существующей в газе. Во многих других случаях, однако, даже приблизительно не выполнено условие доминирования упругих соударений над всеми другими процессами. Это верно, например, в физике ионосферы и космической плазмы, где процессы рекомбинации и столкновительного возбуждения (то есть излучательные процессы) имеют большое значение, в особенности для электронов. Предположение о применимости распределения Максвелла дало бы в этом случае не только количественно неверные результаты, но даже предотвратило бы правильное понимание физики процессов на качественном уровне. Также, в том случае где квантовая де Бройлева длина волны частиц газа не является малой по сравнению с расстоянием между частицами, будут наблюдаться отклонения от распределения Максвелла из-за квантовых эффектов. Распределение энергии Максвелла может быть выражено как дискретное распределение энергии:
где Распределение Больцмана. Распределение Больцмана — распределение вероятностей различных энергетических состояний идеальной термодинамической системы (идеальный газ атомов или молекул) в условиях термодинамического равновесия; открыто Л. Больцманом в 1868—1871. Согласно распределению Больцмана среднее число частиц с полной энергией
где
В случае, когда движение частиц подчиняется классической механике, энергию
Явление переноса. Диффузия В термодинамически неравновесных системах происходят особые необратимые процессы, называемые явлениями переноса, в результате которых осуществляется пространственный перенос массы, импульса, энергии. К явлениям переноса относятся теплопроводность (перенос энергии), диффузия (перенос массы) и внутреннее трение (перенос импульса). Ограничимся одномерными явлениями переноса. Систему отсчета будем выберать так, чтобы ось х была направлена в сторону в направления пер Диффузия. При происходит самопроизвольное проникновение и перемешивание частиц двух соприкасающихся газов, жидкостей и даже твердых тел; диффузия есть обмен масс частиц этих тел, при этом явление возникает и продолжается, пока существует градиент плотности. Во времена становления молекулярно-кинетической теории по вопросу явления диффузии возникли противоречия. Поскольку молекулы перемещаются в пространстве с огромными скоростями, то диффузия должна происходить очень быстро. Если же открыть в комнате крышку сосуда с пахучим веществом, то запах распространяется довольно медленно. Но здесь нет противоречия. При атмосферном давлении молекулы обладают малой длиной свободного пробега и, при столкновениях с другими молекулами, приемущественно «стоят» на месте. Явление диффузии для химически однородного газа подчиняется закону Фика:
где jm — плотность потока массы — величина, определяемая массой вещества, диффундирующего в единицу времени через единичную площадку, перпендикулярную оси х, D — диффузия (коэффициент диффузии), dρ/dx — градиент плотности, который равен скорости изменения плотности на единицу длины х в направлении нормали к этой площадке. Знак минус говорит о том, что перенос массы происходит в направлении убывания плотности (поэтому знаки jm и dρ/dx противоположны). Диффузия D численно равна плотности потока массы при градиенте плотности, равном единице. Согласно кинетической теории газов,
Явление переноса. Вязкость В термодинамически неравновесных системах происходят особые необратимые процессы, называемые явлениями переноса, в результате которых осуществляется пространственный перенос массы, импульса, энергии. К явлениям переноса относятся теплопроводность (перенос энергии), диффузия (перенос массы) и внутреннее трение (перенос импульса). Ограничимся одномерными явлениями переноса. Систему отсчета будем выберать так, чтобы ось х была направлена в сторону в направления переноса. Внутреннее трение (вязкость). Суть механизма возникновения внутреннего трения между параллельными слоями газа (жидкости), которые движущутся с различными скоростями, есть в том, что из-за хаотического теплового движения осуществляется обмен молекулами между слоями, в результате чего импульс слоя, который движется быстрее, уменьшается, который движется медленнее — увеличивается, что приводит к торможению слоя, который движется быстрее, и ускорению слоя, который движется медленнее. Как известно, сила внутреннего трения между двумя слоями газа (жидкости) подчиняется закону Ньютона:
где η — динамическая вязкость (вязкость), d ν /dx — градиент скорости, который показывает быстроту изменения скорости в направлении х, перпендикулярном направлению движения слоев, S — площадь, на которую действует сила F. Согласно второму закону Ньютона взаимодействие двух слоев можно рассматривать как процесс, при котором в единицу времени от одного слоя к другому передается импульс, который по модулю равен действующей силе. Тогда выражение (5) можно записать в виде
Динамическая вязкость η численно равна плотности потока импульса при градиенте скорости, равном единице; она вычисляется по формуле
Из сопосавления формул (1), (3) и (6), которые описывают явления переноса, следует, что закономерности всех явлений переноса сходны между собой. Эти законы были известны еще задолго до того, как они были обоснованы и получены из молекулярно-кинетической теории, которая позволила установить, что внешнее сходство их математических выражений является следствием общностью лежащего в основе явлений теплопроводности, диффузии и внутреннего трения молекулярного механизма перемешивания молекул в процессе их хаотического движения и столкновений друг с другом. Рассмотренные законы Фурье, Фика и Ньютона не вскрывают молекулярно-кинетической сути коэффициентов λ, D и η. Выражения для коэффициентов переноса получаются из кинетической теории. Они записаны без вывода, поскольку строгое и формальное рассмотрение явлений переноса довольно громоздко, а качественное — не имеет смысла. Формулы (2), (4) и (7) дают связь коэффициентов переноса и характеристики теплового движения молекул. Из этих формул следуют простые зависимости между λ, D и η:
Начала термодинамики. Начала термодинамики — совокупность постулатов, лежащих в основе термодинамики. Эти положения были установлены в результате научных исследований и были доказаны экспериментально. В качестве постулатов они принимаются для того, чтобы термодинамику можно было построить аксиоматически. Необходимость начал термодинамики связана с тем, что термодинамика описывает макроскопические параметры систем без конкретных предположений относительно их микроскопического устройства. Вопросами внутреннего устройства занимается статистическая физика. Начала термодинамики независимы, то есть ни одно из них не может быть выведено из других начал. Перечень начал термодинамики
|
||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 388; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.009 с.) |

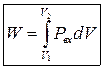 w – работа, р – давление, d(дельта)V – изменение объема
w – работа, р – давление, d(дельта)V – изменение объема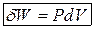
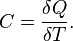
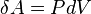
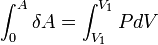 ,
, .
.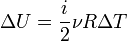 ,
,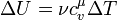 ,
,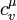 — молярная теплоёмкость при постоянном объёме.
— молярная теплоёмкость при постоянном объёме.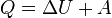
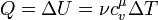 ,
,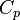 . В идеальном газе она связана с теплоёмкостью при постоянном объёме соотношением Майера
. В идеальном газе она связана с теплоёмкостью при постоянном объёме соотношением Майера 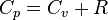 .
.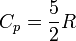 , то есть около 20.8 Дж/(моль·К);
, то есть около 20.8 Дж/(моль·К);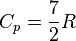 , то есть около 29.1 Дж/(моль·К);
, то есть около 29.1 Дж/(моль·К);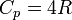 , то есть около 33.3 Дж/(моль·К).
, то есть около 33.3 Дж/(моль·К).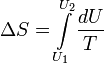 . В случае, если изобарный процесс происходит в идеальном газе, то
. В случае, если изобарный процесс происходит в идеальном газе, то 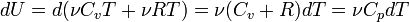 , следовательно, изменение энтропии можно выразить как
, следовательно, изменение энтропии можно выразить как 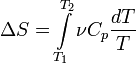 . Если пренебречь зависимостью
. Если пренебречь зависимостью 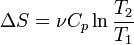
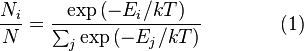 ,
,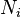 является числом молекул имеющих энергию
является числом молекул имеющих энергию 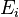 при температуре системы
при температуре системы 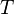 ,
, 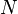 является общим числом молекул в системе и
является общим числом молекул в системе и 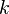 — постоянная Больцмана. (Отметьте, что иногда вышеупомянутое уравнение записывается с множителем
— постоянная Больцмана. (Отметьте, что иногда вышеупомянутое уравнение записывается с множителем 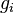 , обозначающим степень вырождения энергетических уровней. В этом случае сумма будет по всем энергиям, а не всем состояниям системы). Поскольку скорость связана с энергией, уравнение (1) может использоваться для получения связи между температурой и скоростями молекул в газе. Знаменатель в уравнении (1) известен как каноническая статистическая сумма.
, обозначающим степень вырождения энергетических уровней. В этом случае сумма будет по всем энергиям, а не всем состояниям системы). Поскольку скорость связана с энергией, уравнение (1) может использоваться для получения связи между температурой и скоростями молекул в газе. Знаменатель в уравнении (1) известен как каноническая статистическая сумма. равно
равно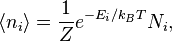
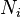 — кратность состояния частицы с энергией
— кратность состояния частицы с энергией 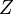 находится из условия, что сумма
находится из условия, что сумма 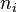 по всем возможным значениям
по всем возможным значениям 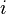 равна заданному полному числу частиц
равна заданному полному числу частиц 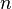 в системе (условие нормировки):
в системе (условие нормировки):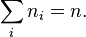
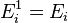 (кин) частицы (молекулы или атома),
(кин) частицы (молекулы или атома), 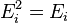 (вн) (например, энергии возбуждения электронов) и
(вн) (например, энергии возбуждения электронов) и 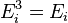 (пот) во внешнем поле, зависящей от положения частицы в пространстве:
(пот) во внешнем поле, зависящей от положения частицы в пространстве: 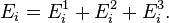
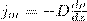 (3)
(3)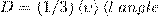 (4)
(4) (5)
(5) (6)
(6)  (7)
(7) и
и 



