
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Круговой процесс. Цикл КарноСодержание книги Поиск на нашем сайте Круговой процесс — процесс, при котором газ, пройдя через ряд состояний, возвращается в исходное. Цикл Карно́ — это обратимый круговой процесс, состоящий из двух адиабатических и двух изотермических процессов[1]. В процессе Карно термодинамическая система выполняет механическую работу и обменивается теплотой с двумя тепловыми резервуарами, имеющими постоянные, но различающиеся температуры. Резервуар с более высокой температурой называется нагревателем, а с более низкой температурой — холодильником[2]. Основное уравнение молекулярно-кинетической теории газа.
Средняя кинетическая энергия молекул газа
Средняя кинетическая энергия теплового движения молекул газа. Уравнение состояния идеального газа в форме pV = n RT или p = nkT может быть обосновано и методами кинетической теории газов. На основе кинетического подхода сравнительно просто выводится выражение для давления идеального газа в сосуде, которое получается как результат усреднения импульсов молекул, передаваемых стенке сосуда при многочисленных соударениях молекул со стенкой. Величина получаемого при этом давления определяется как
Где б v 2с – среднее значение квадрата скорости молекул, m – масса молекулы. Средняя кинетическая энергия молекул газа (в расчете на одну молекулу) определяется выражением
Кинетическая энергия поступательного движения атомов и молекул, усредненная по огромному числу беспорядочно движущихся частиц, является мерилом того, что называется температурой. Если температура T измеряется в градусах Кельвина (К), то связь ее с Ek дается соотношением
Это соотношение позволяет, в частности, придать более отчетливый физический смысл постоянной Больцмана Внутренняя энергия идеального газа. В теории идеального газа потенциальная энергия взаимодействия молекул считается равной нулю. Поэтому внутренняя энергия идеального газа определяется кинетической энергией движения всех его молекул. Средняя энергия движения одной молекулы равна
Так как в одном киломоле содержится
Для любой массы m газа, т.е. для любого числа киломолей
Из этого выражения следует, что внутренняя энергия является однозначной функцией состояния и, следовательно, при совершении системой любого процесса, в результате которого система возвращается в исходное состояние, полное изменение внутренней энергии равно нулю. Математически это записывается в виде тождества
Распределение Максвелла Распределение Ма́ксвелла — распределение вероятности, встречающееся в физике и химии. Оно лежит в основании кинетической теории газов, которая объясняет многие фундаментальные свойства газов, включая давление и диффузию. Распределение Максвелла также применимо для электронных процессов переноса и других явлений. Распределение Максвелла применимо к множеству свойств индивидуальных молекул в газе. О нём обычно думают как о распределении энергий молекул в газе, но оно может также применяться к распределению скоростей, импульсов, и модуля импульсов молекул. Также оно может быть выражено как дискретное распределение по множеству дискретных уровней энергии, или как непрерывное распределение по некоторому континууму энергии. Распределение Максвелла может и должно быть получено при помощи статистической механики (см. происхождение статсуммы). Как распределение энергии, оно соответствует самому вероятному распределению энергии, в столкновительно-доминируемой системе, состоящей из большого количества невзаимодействующих частиц, в которой квантовые эффекты являются незначительными. Так как взаимодействие между молекулами в газе является обычно весьма небольшим, распределение Максвелла даёт довольно хорошее приближение ситуации, существующей в газе. Во многих других случаях, однако, даже приблизительно не выполнено условие доминирования упругих соударений над всеми другими процессами. Это верно, например, в физике ионосферы и космической плазмы, где процессы рекомбинации и столкновительного возбуждения (то есть излучательные процессы) имеют большое значение, в особенности для электронов. Предположение о применимости распределения Максвелла дало бы в этом случае не только количественно неверные результаты, но даже предотвратило бы правильное понимание физики процессов на качественном уровне. Также, в том случае где квантовая де Бройлева длина волны частиц газа не является малой по сравнению с расстоянием между частицами, будут наблюдаться отклонения от распределения Максвелла из-за квантовых эффектов. Распределение энергии Максвелла может быть выражено как дискретное распределение энергии:
где Распределение Больцмана. Распределение Больцмана — распределение вероятностей различных энергетических состояний идеальной термодинамической системы (идеальный газ атомов или молекул) в условиях термодинамического равновесия; открыто Л. Больцманом в 1868—1871. Согласно распределению Больцмана среднее число частиц с полной энергией
где
В случае, когда движение частиц подчиняется классической механике, энергию
Явление переноса. Диффузия В термодинамически неравновесных системах происходят особые необратимые процессы, называемые явлениями переноса, в результате которых осуществляется пространственный перенос массы, импульса, энергии. К явлениям переноса относятся теплопроводность (перенос энергии), диффузия (перенос массы) и внутреннее трение (перенос импульса). Ограничимся одномерными явлениями переноса. Систему отсчета будем выберать так, чтобы ось х была направлена в сторону в направления пер Диффузия. При происходит самопроизвольное проникновение и перемешивание частиц двух соприкасающихся газов, жидкостей и даже твердых тел; диффузия есть обмен масс частиц этих тел, при этом явление возникает и продолжается, пока существует градиент плотности. Во времена становления молекулярно-кинетической теории по вопросу явления диффузии возникли противоречия. Поскольку молекулы перемещаются в пространстве с огромными скоростями, то диффузия должна происходить очень быстро. Если же открыть в комнате крышку сосуда с пахучим веществом, то запах распространяется довольно медленно. Но здесь нет противоречия. При атмосферном давлении молекулы обладают малой длиной свободного пробега и, при столкновениях с другими молекулами, приемущественно «стоят» на месте. Явление диффузии для химически однородного газа подчиняется закону Фика:
где jm — плотность потока массы — величина, определяемая массой вещества, диффундирующего в единицу времени через единичную площадку, перпендикулярную оси х, D — диффузия (коэффициент диффузии), dρ/dx — градиент плотности, который равен скорости изменения плотности на единицу длины х в направлении нормали к этой площадке. Знак минус говорит о том, что перенос массы происходит в направлении убывания плотности (поэтому знаки jm и dρ/dx противоположны). Диффузия D численно равна плотности потока массы при градиенте плотности, равном единице. Согласно кинетической теории газов,
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 401; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.008 с.) |

 - основное уравнение МКТ идеального газа. Выведено в предположении, что давление газа есть результат ударов его молекул о стенки сосуда. Это же уравнение в другой записи:
- основное уравнение МКТ идеального газа. Выведено в предположении, что давление газа есть результат ударов его молекул о стенки сосуда. Это же уравнение в другой записи: 
 Средняя кинетическая энергия молекул идеального газа. Другие формулы, где встречается средняя энергия молекул идеального газа:
Средняя кинетическая энергия молекул идеального газа. Другие формулы, где встречается средняя энергия молекул идеального газа: 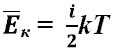 Средняя энергия движения молекул и температура.
Средняя энергия движения молекул и температура. 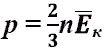 Основное уравнение МКТ идеального газа
Основное уравнение МКТ идеального газа
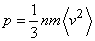 ,
,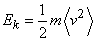


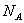 молекул, то внутренняя энергия одного киломоля газа будет
молекул, то внутренняя энергия одного киломоля газа будет
 , получим
, получим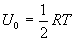
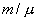 внутренняя энергия
внутренняя энергия
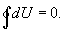
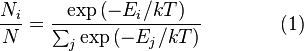 ,
,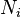 является числом молекул имеющих энергию
является числом молекул имеющих энергию 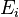 при температуре системы
при температуре системы 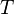 ,
, 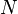 является общим числом молекул в системе и
является общим числом молекул в системе и 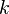 — постоянная Больцмана. (Отметьте, что иногда вышеупомянутое уравнение записывается с множителем
— постоянная Больцмана. (Отметьте, что иногда вышеупомянутое уравнение записывается с множителем 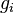 , обозначающим степень вырождения энергетических уровней. В этом случае сумма будет по всем энергиям, а не всем состояниям системы). Поскольку скорость связана с энергией, уравнение (1) может использоваться для получения связи между температурой и скоростями молекул в газе. Знаменатель в уравнении (1) известен как каноническая статистическая сумма.
, обозначающим степень вырождения энергетических уровней. В этом случае сумма будет по всем энергиям, а не всем состояниям системы). Поскольку скорость связана с энергией, уравнение (1) может использоваться для получения связи между температурой и скоростями молекул в газе. Знаменатель в уравнении (1) известен как каноническая статистическая сумма. равно
равно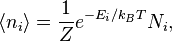
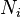 — кратность состояния частицы с энергией
— кратность состояния частицы с энергией 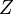 находится из условия, что сумма
находится из условия, что сумма 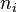 по всем возможным значениям
по всем возможным значениям 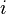 равна заданному полному числу частиц
равна заданному полному числу частиц 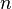 в системе (условие нормировки):
в системе (условие нормировки):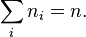
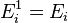 (кин) частицы (молекулы или атома),
(кин) частицы (молекулы или атома), 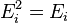 (вн) (например, энергии возбуждения электронов) и
(вн) (например, энергии возбуждения электронов) и 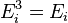 (пот) во внешнем поле, зависящей от положения частицы в пространстве:
(пот) во внешнем поле, зависящей от положения частицы в пространстве: 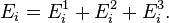
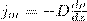 (3)
(3)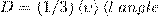 (4)
(4)


