
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Работа и теплота. Свойства работы и теплоты.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Введем обозначения: A – абсолютная работа, Q – теплота. Различают не только механическую(деформационную), но и немеханическую(например: работа химических реакций, работа электрических и магнитных сил). Примечание: в дальнейшем, во всех формулах термодинамики используются удельные величины, то есть величины отнесенные у 1 кг системы, при этом размерность А[ Как было установлено в ходе развития науки, работа и теплота- это единственные формы передачи энергии, то есть работа и теплота проявляются только в процессе передачи энергии, поэтому термины «механическая энергия», «тепловая энергия» не являются точными. Как было показано ранее внутренняя энергия системы U является ожнозначной функцией всей совокупности координат состояния системы, то есть: U = U(x1, x2,…,xn) (17) Если бы условие (17) не выполнилось, то стал бы возможным вечный двигатель первого рода, то есть двигатель, творящий работу без подвода энергии извне. Внутренняя энергия является функцией состояния, то есть ее изменение при переходе из начального состояния в конечное не зависит от пути перехода и определяется как разность значений в этих состояниях. DU = U2 – U1. Ранее было получено первое начало термодинамики в общем виде
Qk- общее обозначение количества воздействия при k-том взаимодействии Исходя из того, что единственным источником теплоты является внутренняя энергия системы (U), то выделим в правой части уравнения (1) отдельное слагаемое, соответствующее тепловому взаимодействию:
Как известно, для всех взаимодействий, кроме теплового, справедливо следующее выражение: dAk = –dQk, где Ak – работа при k-том взаимодействии (механическая и немеханическая).
Обозначим dU = dQ – dA (18) формула (18)- это первое начало термодинамики в обычной форме. Или dQ = dU + dA (18*) После интегрирования, уравнение (18*) запишется следующим образом: Q=∆U+A (19) Из уравнения (19)следует простоя формулировка первого закона термодинамики: подведённая к системе теплота идёт на изменение внутренней энергии системы и на совершение системой работы против внешних сил. Правило знаков для работы: Работа считается положительной, если она совершается против внешних сил (например, работа расширения) и работа считается отрицательной, если работа ведется над системой (работа сжатия).
Теплота и работа, в отличие от внутренней работы, не являются функциями состояния, а являются функциями процесса. Этот тезис иллюстрируется следующими графиками:
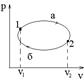
Амех= Q= Из (20) следует, что графически, работа процесса в координатах PV изображается как площадь под кривой процесса. Из уравнения (21) следует, что теплота которой обмениваются система и окружающая среда в процессах TS координатах изображается в TS координатах как площадь под кривой процесса. Цикл- это круговой процесс, в котором система возвращается в исходное состояние. Например:
Циклы происходящие по часовой стрелке- прямые, против часовой стрелки- обратные. Так как внутренняя энергия U является функцией состояния, то ее изменение в этом цикле DU1-а-2-б-1=0 или
Из математики известно, что
Пример (из другой области):Eпот=mgH – независима от пути подъёма груза на высоту H. Исследование принадлежности A и Q к функциям состояния проще всего провести на примере деформационной системы:
1) оба интеграла имеют нулевые значения; 2) иначе, Деформационная система имеет одну степень свободы. Рассмотрим произвольный процесс, который совершает система:
dQk = - dAk dAдеф = P dv
Так как работа A и теплота Q не являются функциями состояния, то круговой интеграл
Характеристические функции.
Все характеристические функции являются функциями состояния. Функция называется характеристической, если её частная производная по некоторому параметру даёт другой параметр, а именно, соответствующий тому, по которому производится дифференцирование. 1. Рассмотрим сопряжение по координатам: В этом случае, в качестве независимо изменяющихся параметров выступают только координаты, а потенциалы отслеживают их изменение по каким-либо зависимостям.
Как было показано ранее, внутренняя энергия является функцией состояния и полностью определяется всей совокупностью координат состояния системы. U=U(X1, X2,…, Xn) (17) Дифференциалы всех функций состояния являются полными дифференциалами, поэтому dU- полный дифференциал. В соответствии с правилами математики нахождение полного дифференциала функции нескольких переменных
Xinv – означает, что все остальные координаты инвариантны, т.е. не являются переменными (замороженными).
Из первого начала термодинамики в общем виде (3) и формулы (23) следует равенство правых частей.
Так как данное равенство должно выполняться при любом k, то получаем
Из сравнения полученного выражения формулы (24) и определения характеристической функции следует вывод о том, что внутренняя энергия является характеристической функцией при сопряжении по координатам. Введем общее обозначение характеристической функции Y(пси). Y(Xk)=U (25) Дифференциалом этой характеристической функции является первое начало термодинамики в общем виде. В качестве примера рассмотрим термодеформационную систему.
Y(S,v)=U
Из первого начала термодинамики получается
dU=TdS–pdv (28) (28)- первое начало термодинамики в обычной форме для термодеформационной системы. В общем случае (для любой системы) при сопряжении по координатам дифференциальной характеристикой функции определяется по формуле:
dU=dY
2. Рассмотрим сопряжение по потенциалам: При этом виде сопряжения независимым образом изменяются только потенциалы, а координаты отслуживают их изменение по каким-либо конкретным формулам, так как изменяются зависимым образом. Вывод аналогичен случаю 1, можно сразу записать итоговую формулу: 1) 2) 3) Рассмотрим в качестве примера термодеформационную систему:
Из (29) =>Y(T,p) = U – TS + pv – эта характеристическая функция в термодинамике имеет обозначение и название F=U–TS+pv (32) (32)– свободная энтальпия (удельная свободная энтальпия); Из(30)=>dF=SdT+vdp (33) По своей сути уравнение (33) это одна из форм первого начала термодинамики. Из(31)=>
Свободная энтальпия – часть энтальпии (i), которая может быть использована в каких-либо технических целях. Энтальпию раньше называли теплосодержанием.
3) Смешанное сопряжение. В этом случае в качестве независимых параметров выступают не все n потенциалов, а только r потенциалов от общего числа. Такие независимые потенциалы будем обозначать: Pi, i=1,2,3,…,r., r <n Независимые координаты обозначим как j=(r+1),(r+2),…,n Опуская вывод (аналогичен случаю 1), сразу запишем окончательное выражение.
Рассмотрим термодеформационную систему
1) Пусть независимым образом изменяется потенциал – Т и независимая координата – v: Тогда из (36) =>Y(T,v) = U – TS Эта характеристическая функция имеет свое обозначение и название. F=U-TS (40) Уравнение (40) это свободная энергия В химической термодинамике F называется изохорно-изотермическим потенциалом. В соответствие с формулой (37) дифференциал этой функции: dF = – S dT – p dv (41) По физической сути это одна из форм первого начала термодинамики. Из формул (38), (39) следует:
Если рассмотреть в формуле (41) изотермический процесс, где T=const, то dFT = – p dv (44) так как dA = p dv, то в соответствии с формулой (44) в изотермических процессах абсолютная работа, совершаемая системой, производится за счёт убыли свободной энергии ∆FT=-AT или: AT= -∆FT (45) Ранее отмечалось, что в изотермических процессах вся подведённая к системе теплота идёт на совершение абсолютной работы. 2) Независимым потенциалом является абсолютной давление (P), а независимой координатой энтропия (S). В соответствии с формулами (36-39) можно записать Y(p,S) = U + pv, эта характеристическая функция называется энтальпией i. i=U+pv[ (46)
По физическому смыслу произведение p на v это потенциальная энергия одного килограмма газа при давлении p и удельного объема v.
S- Площадь поршня M- Масса груза P- Давление в системе (газа под поршнем) W-Объем системы (газа под поршнем) H- Высота поднятия поршня
Eпот = pSH = pW. Если отнести Eпот к 1 кг системы, то Так как внутренняя энергия идеального газа зависит только от температуры и не учитывает давление газа, то энтальпия полнее учитывает энергетические возможности системы с точки зрения совершения работы. Di=VdP+TdS (47) Как известно, TdS=dQ, тогда уравнение примет вид:di=VdP+dQ Рассмотрим частный случай, где P=const (изобарный) Dip=dQp (48) После интегрирования получим ∆ip=i2-i1=Qp или Qp=i2-i1 (49) Из формулы (49) следует, что в изобарных процессах теплота процесса определяется как разность энтальпии, конечного и начального состояния.
Рассмотрим формулу (47) di=VdP+TdS, тогда di=VdP+dQ или dQ=di-VdP (52) Уравнение (52) это первое начало термодинамики в энтальпийной форме. Введем обозначение Aрасп. Располагаемая работа- это работа, которая может быть передана другой системе.
Рассмотрим произвольный процесс расширения системы 1-2
С учетом (53) уравнение (52) запишется как dQ=di+dAрасп (54) Формулировка первого начала термодинамики в энтальпийной форме из (54): Подведенная к системе теплота идее на изменение ее энтальпии и не совершает располагаемой работы.
Мнемонический приём для термодеформационной системы:
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 955; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.57.73 (0.009 с.) |

 ], Q[
], Q[  ].
]. (1)
(1) .
. .
. , тогда
, тогда

 (20)
(20) (21)
(21)
 (22)
(22) .
. , поэтому на поставленный вопрос существует два возможных ответа:
, поэтому на поставленный вопрос существует два возможных ответа: .
.
 dQдеф = - P dv
dQдеф = - P dv
 , т.е.
, т.е.  .
. ,
, 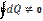 , то есть dA и dQ не являются полными дифференциалами, и этот факт иногда отражают обозначениями вида đA,đQ.
, то есть dA и dQ не являются полными дифференциалами, и этот факт иногда отражают обозначениями вида đA,đQ.

 (23)
(23) =
= 
 (24)
(24) (26)
(26) (27)
(27) )=
)= 
 (29)
(29) (30)
(30) (31)
(31) (34)
(34) (35)
(35)
 (36)
(36) (37)
(37) (38)
(38)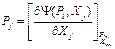 (39)
(39) (42)
(42) (43)
(43)

 (50)
(50) (51)
(51) (53)
(53)




 , и т.д.
, и т.д.


