
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 1. Техническая термодинамикаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1 Основные понятия и определения термодинамики
Термодинамика, наука о взаимопревращениях различных видов энергии. Различают общую (физическую), химическую и техническую термодинамику. Техническая термодинамика, наука, изучающая закономерности взаимного превращения теплоты и работы в технических устройствах различного назначения. Энергия, общая количественная мера различных форм движения материи. Размерность Дж или Дж/кг. Работа, форма преобразования энергии в результате макроскопического перемещения тел. Количество преобразованной в этом случае энергии называют количеством работы или работой. Обозначается: полная работа L, Дж, удельная работа l, Дж/кг. Различают: работу изменения объема Теплота, форма преобразования энергии в результате микроскопического движения тел. Количество преобразованной в этом случае энергии называется количеством теплоты или теплотой. Обозначается: полная теплота Q, Дж, удельная теплота q, Дж/кг. Рабочее тело, вещество, посредством которого происходит взаимопревращение теплоты и работы. Термодинамическая система (система), совокупность тел, участвующих в процессах переноса (преобразования) энергии. Окружающая среда, совокупность тел, не входящих в термодинамическую систему. Открытая система, система, в которой имеет место обмен вещества с окружающей средой. Закрытая система, система, в которой отсутствует обмен вещества с окружающей средой. Адиабатная система, система, в которой отсутствует теплообмен с окружающей средой. Изолированная система, система, которая не обменивается энергией и веществом с окружающей средой. Термодинамические параметры состояния, физические величины, однозначно характеризующие состояние термодинамической системы. Различают термические и калорические параметры состояния. Термические параметры состояния: давление, удельный объем, температура. Калорические параметры состояния(функции состояния): внутренняя энергия, энтальпия, энтропия. Экстенсивные термодинамические параметры, параметры, зависящие от массы вещества, например, внутренняя энергия, энтальпия, энтропия. Интенсивные термодинамические параметры, параметры, не зависящие от массы вещества, например, давление, температура. Удельный объем, объем единицы массы вещества, v = V / M, м3/кг. Мольный объем, объем моля (киломоля) вещества, V m = V / N, м3/кмоль. Плотность, масса единицы объема вещества, r = M / V = 1/ v, кг/м3. Температура, мера интенсивности теплового движения микрочастиц вещества (атомов, молекул, ионов). Температуру, измеренную по шкале Цельсия, обозначают t, оС. Термодинамическая (абсолютная) температура, температура, отсчитываемая по термодинамической шкале температур (шкале Кельвина) от абсолютного нуля. Обозначают Т К. Связь между температурами по шкале Цельсия и Кельвина: Т = t + 273. Абсолютное давление (давление), отношение силы, действующей по нормали к поверхности тела, к площади этой поверхности. Обозначают р, Н/м2 (1 Н/м2 = 1 Па, 106 Па = 1 МПа, 103 Па = 1 кПа). Существуют другие единицы измерения давления, связь между некоторыми из них следующая: 1 ат = 1 кг/см2 = 0,981 бар = 98100 Па = 735,5 мм рт. ст. = 104 мм вод. ст. Разность между абсолютным давлением и барометрическим (атмосферным) называют избыточным давлением. Это давление не является параметром состояния. Нормальные условия, условия, реализуемые при температуре t = 0 oC и давлении р = 101325 Па. Уравнение состояния, уравнение, связывающее между собой термодинамические параметры системы в равновесном состоянии. Например, термическое уравнение состояния связывает давление, температуру и удельный объем: F (p, v, T) = 0. Равновесное состояние, состояние системы, характеризующееся равенством термодинамических параметров во всех её частях. Неравновесное состояние, состояние системы, характеризующееся неравенством термодинамических параметров во всех её частях. Термодинамический процесс, последовательность изменяющихся состояний термодинамической системы. Равновесный процесс, процесс, рассматриваемый как непрерывный ряд равновесных состояний системы. Неравновесный процесс, процесс, рассматриваемый как непрерывный ряд неравновесных состояний системы. Любой реальный процесс является неравновесным. Если скорость осуществления неравновесного процесса бесконечно мала, его можно рассматривать как равновесный процесс. Обратимый процесс, процесс, в результате совершения которого в прямом и обратном направлениях, система возвращается в начальное состояние без изменений в окружающей среде. Равновесные процессы обратимы. Необратимый процесс, процесс, в результате совершения которого в прямом и обратном направлениях, система не возвращается в начальное состояние без дополнительной затраты энергии. Неравновесные процессы необратимы. Термодинамическая диаграмма, диаграмма, в которой по осям координат откладывают значения термодинамических параметров или функций состояния (pv -диаграмма, Ts -диаграмма и т. д.). В диаграммах можно изображать равновесные термодинамические процессы. Например, 1-2 – процесс расширения (dv > 0). Так как работа изменения объема газа
Уравнение состояния идеального газа, уравнение Клапейрона pV = MRT или уравнение Менделеева-Клапейрона Универсальная газовая постоянная, постоянная для всех идеальных газов (m R), входящая в уравнение Менделеева-Клапейрона. Численно равна m R = 8314,34 Дж/(кмоль×К). Газовая постоянная, характерная для каждого идеального газа постоянная (R), входящая в уравнение Клапейрона. Численно равна работе изменения объема 1 кг газа в изобарном процессе при изменении температуры на 1К. Может быть определена из выражения R = 8314/m Дж/(кг×К), где m – молекулярная масса газа. Смесь идеальных газов, механическая смесь химически не взаимодействующих газов. Каждый компонент смеси является идеальным газом. Закон Дальтона, закон, определяющий поведение смеси идеальных газов. Утверждает: каждый компонент ведет себя в газовой смеси так, как будто он один при температуре смеси занимает весь объем смеси. Парциальный объем, объем, который имел бы газ, входящий в газовую смесь, если бы он находился при давлении и температуре смеси. Сумма парциальных объемов компонентов смеси равна объему смеси. Парциальное давление, давление, который имел бы газ, входящий в газовую смесь, если бы он имел объем смеси при температуре смеси. Сумма парциальных давлений компонентов смеси равна давлению смеси. Концентрация, величина, характеризующая относительное содержание компонента в смеси. Объемная доля (концентрация), отношение парциального объема компонента (Vi) к объему смеси (Vсм): ri = Vi / Vсм. Массовая доля (концентрация), отношение массы компонента (Мi) к массе смеси (Мсм): gi = Mi / Mсм. Мольная доля (концентрация), отношение количества молей компонента (Ni) к общему количеству молей смеси (Nсм): xi = Ni / Nсм. Кажущаяся молекулярная масса смеси, условная величина, позволяющая проводить расчеты со смесью идеальных газов как с однокомпонентным рабочим телом. В зависимости от способа задания состава смеси рассчитывают по формулам: Газовая постоянная смеси, условная для смеси идеальных газов постоянная (Rсм), входящая в уравнение Клапейрона. Определяют из выражения: Теплоемкость, количество теплоты, необходимое для изменения температуры тела на 1 К. Обозначается С, Дж/К. Удельная теплоемкость, теплоемкость единицы количества вещества. Теплоемкость единицы массы вещества (1 кг) называют массовой удельной теплоемкостью или просто массовой теплоемкостью: с, Дж/(кг×К). Теплоемкость единицы объема при нормальных условиях называют объемной теплоемкостью: с ', Дж/(м3н×К). Теплоемкость 1 кмоля вещества называют мольной (или молярной) теплоемкостью: m с, Дж/(кмоль×К). Связь между удельными теплоемкостями: с = m с /m, с ' = m с /22,4 = r н × с,m с = с '×22,4. Средняя теплоемкость, теплоемкость (ст), отнесенная к интервалу температур D Т = Т 2 – Т 1. Определяют из выражения: ст = q /(T 2 – T 1). Истинная теплоемкость, теплоемкость, соответствующая бесконечно малому изменению температуры dT: с = dq / dT. Изобарная теплоемкость, теплоемкость в изобарном (p = const) термодинамическом процессе. Обозначают ср, ср ', m ср. Изохорная теплоемкость, теплоемкость в изохорном (v = const) термодинамическом процессе. Обозначают сv, сv ', m сv. Уравнение Майера, уравнение, устанавливающее связь между изобарной и изохорной теплоемкостью идеального газа: ср – сv = R или m ср – m сv = m R = 8314. Теплоемкость смеси идеальных газов, теплоемкость, определяемая суммой произведения концентрации компонентов на соответствующую теплоемкость компонента. В зависимости от способа задания состава смеси теплоемкость смеси определяют по формулам:
Первый закон термодинамики
Первый закон термодинамики, утверждает, что энергия не исчезает и не возникает вновь, она лишь переходит из одного вида в другой в различных физических и химических процессах. Применительно к задачам технической термодинамики, аналитическое выражение первого закона может быть представлено в виде:
Внутренняя энергия, функция состояния системы, характеризующаяся тем, что её величина включает все виды кинетической и потенциальной энергии микрочастиц вещества. Обозначают: полная внутренняя энергия U, Дж, удельная внутренняя энергия u = U / M, Дж/кг. Изменение внутренней энергии в процессе не зависит от пути его протекания, а определяется только начальным и конечным состояниями. Для идеального газа изменение внутренней энергии в процессе зависит только от температуры и определяется из выражения: Энтальпия, функция состояния системы, определяемая суммой внутренней энергии и произведения объема на давление в системе. Обозначают: полная энтальпия Энтропия, функция состояния системы, дифференциал которой в равновесном процессе равен отношению бесконечно малого количества теплоты (dQ или dq), сообщенной системе, к термодинамической температуре (Т) системы. Обозначают: полная энтропия
Второй закон термодинамики
Второй закон термодинамики, утверждает, что любой реальный самопроизвольный процесс является необратимым. Это означает, что теплота не может сама собой переходить от более холодного тела к более нагретому. Аналитическое выражение второго закона: Цикл (круговой процесс), замкнутый термодинамический процесс, в результате которого рабочее тело возвращается в исходное состояние. Прямой цикл, цикл, полезным энергетическим результатом которого является преобразование части подведенной извне теплоты в работу. Эти циклы реализуют в тепловых двигателях. Обратный цикл, цикл, полезным энергетическим результатом которого является перенос теплоты от тела с меньшей температурой к телу с большей температурой. Эти циклы реализуют в холодильных машинах и тепловых насосах. Обратимый цикл, цикл, состоящий из обратимых процессов. Необратимый цикл, цикл, в котором хотя бы один процесс является необратимым. Термический коэффициент полезного действия (КПД), отношение работы(lц), полученной в результате осуществления прямого цикла, к теплоте, подведенной к рабочему телу (q 1). Обозначают: Холодильный коэффициент, отношение теплоты (q 2), отведенной в обратном цикле от охлаждаемого объекта, к затраченной в цикле работе (lц). Обозначают:
Если рассматривать указанный цикл в обратном направлении (1-4-3-2-1), то это обратимый обратный цикл Карно. Показателем эффективности такого цикла может служить холодильный коэффициент: Свойства обратимых циклов, для любого обратимого цикла интеграл Свойства необратимых циклов, для любого необратимого цикла интеграл Принцип возрастания энтропии, в изолированной системе (dq = 0) ds ³ 0. Знак равенства относится к обратимым процессам, а знак неравенства к необратимым процессам. Поскольку все реальные процессы необратимы, то энтропия изолированной системы всегда возрастает, стремясь к максимуму. Максимум энтропии соответствует состоянию равновесия, когда в системе не остается разностей температур, и становятся невозможными самопроизвольные процессы. Обобщенный (регенеративный) цикл Карно, цикл, состоящий из двух изотерм и двух эквидистантных (равноудаленных) кривых. Характерен тем, что, не являясь циклом Карно, имеет такой же термический КПД. Регенерация – метод повышения эффективности реальных циклов тепловых машин. Эксергия, максимально возможная работа, которая может быть произведена телом в результате его взаимодействия с окружающей средой. Обозначают: полная эксергия Е, Дж, удельная эксергия е, Дж/кг. Эксергия рабочего тела, максимальная работа, которую может совершить тело с внутренней энергией и в системе с окружающей средой: Эксергия потока рабочего тела, максимальная работа, которая может быть получена от потока вещества с энтальпией h при его взаимодействии с окружающей средой: Эксергия теплоты, максимальная работа, которая может быть получена за счет источника теплоты q со средней температурой Т при условии, что холодным источником является окружающая среда с температурой Т 0: Эксергетический КПД, отношение полезно используемой эксергии (еполезн), к затрачиваемой эксергии (езатр): h е = еполезн / езатр.
Термодинамические процессы Изохорный процесс, процесс, протекающий при постоянном объеме. Уравнение процесса v = const. Основные формулы для расчета изохорного процесса с идеальным газом:
 ; ;  ; ;  ; ;  ; l = 0; ; l = 0;  ; ; 
Изобарный процесс, процесс, протекающий при постоянном давлении. Уравнение процесса р = const. Основные формулы для расчета изобарного процесса с идеальным газом:
Изотермический процесс, процесс, протекающий при постоянной температуре. Уравнение процесса Т = const. Основные формулы для расчета изотермического процесса с идеальным газом:
q = 0; s = const;
Качественные особенности реальных газов. Исследования свойств реальных газов в широком диапазоне термодинамических параметров показали, что свойства таких газов отклоняются от законов, справедливых для идеальных газов, тем значительнее, чем выше их плотность. Молекулы реальных газов в отличие от идеальных газов имеют определенные (конечные) размеры, и между ними существуют силы межмолекулярного взаимодействия. При определенных условиях эти силы могут приводить к ассоциации или диссоциации молекул, что существенно отражается на свойствах газа. При малых межмолекулярных расстояниях внутренние силы могут действовать как силы отталкивания и создавать внутреннее давление. При значительных расстояниях между молекулами действуют главным образом силы взаимного притяжения. В связи с этим поведение термических и калорических свойств реальных газов значительно отличаются от идеальных. Например, коэффициент сжимаемости В отличие от теплоемкости идеальных газов теплоемкости ср и cv реальных газов зависят не только от температуры, но и от давления. Эти зависимости имеют сложный характер. В области низких давлений зависимости изохорной и изобарной теплоемкостей от температуры близки к линейным. При давлениях ниже критического теплоемкости ср и cv возрастают с понижением температуры и приближением к состоянию сжижения, что связано с процессом ассоциации молекул. В области высоких температур влияние температуры оказывается незначительным. Повышение давления в этой области приводит к увеличению теплоемкости. В области сверхкритических давлений изобары теплоемкости проходят через максимум, который с повышением давления смещается в сторону высоких температур. Величина ср (или cv)в точке максимума увеличивается с приближением к ркр. В критической точке изобарная теплоемкость равна бесконечности. Уравнение состояния реальных газов. Для реальных газов предложено много уравнений состояния, но ни одно из них не обладает достаточной общностью и точностью. Физические особенности реальных газов качественно хорошо отражаются уравнением Ван-дер-Ваальса. Оно же является и наиболее простым, единым для жидкой и газовой фаз, термическим уравнением состояния. Ван-дер-Ваальс учел влияние сил взаимодействия молекул и влияние их объема путем введения поправочных факторов в уравнение состояния идеального газа. Это уравнение, полученное на основе, главным образом, умозрительных качественных заключений имеет вид Гетерогенная система, система, состоящая из различных по своим свойствам частей, разграниченных поверхностями раздела (лед-вода, вода-пар). Гомогенная система, система, между любыми частями которой нет поверхностей раздела (пар, вода, лед). Фаза, гомогенная часть гетерогенной системы, ограниченная поверхностью раздела. Фазовый переход, переход вещества из одного фазового состояния в другое. Парообразование, переход вещества из жидкого состояния в газообразное (пар). Испарение, парообразование, происходящее только на свободной поверхности жидкости при любой температуре. Кипение, парообразование, происходящее во всем объеме жидкости в результате подвода теплоты при температуре кипения. Конденсация, переход вещества из газообразного состояния в жидкое в результате отвода теплоты при температуре кипения. Сублимация, переход вещества из твердого состояния в газообразное в результате подвода теплоты при температуре сублимации. Для воды этот процесс возможен при давлениях ниже давления в тройной точке (< 610,8 Па). Процесс перехода вещества из газообразного состояния в твердое, называют десублимацией. Плавление, переход вещества из твердого состояния в жидкое в результате подвода теплоты при температуре плавления. Процесс перехода вещества из жидкого состояния в твердое, называют затвердеванием (кристаллизацией). Температура фазового перехода, температура вещества в процессе равновесного фазового перехода при постоянном давлении. Температура кипения (насыщения), температура вещества в процессе равновесного фазового перехода из жидкого состояния в газообразное (пар) при постоянном давлении. Обозначают tн или ts. При этой же температуре происходит конденсация. Теплота фазового перехода, количество теплоты, которое необходимо подвести или отвести при равновесном изобарно-изотермическом переходе вещества из одной фазы в другую. Теплота парообразования (удельная), т еплота, затраченная на превращение 1 кг кипящей жидкости в сухой насыщенный пар при постоянном давлении. Обозначают r, Дж/кг. Тройная точка, точка на термодинамической диаграмме, соответствующая состоянию, в котором находятся в равновесии три фазы вещества: твердая, жидкая, газообразная. Параметры состояния в тройной точке у различных веществ различны. Для воды: р 0 = 610,8 Па, t 0 = 0,01 оС, v 0 = 0,001 м3/кг. Критическая точка, точка на термодинамической диаграмме, в которой исчезает различие между жидкой и газообразной фазами. Состояние вещества в этом случае называют критическим состоянием. Параметры состояния в критической точке у различных веществ различны. Для воды: рк = 22,115 МПа, tк = 374,12 оС, vк = 3,147 м3/кг. Насыщенный пар, пар, находящийся в равновесии с жидкой фазой. Сухой насыщенный пар, пар, в котором при температуре кипения (насыщения) отсутствуют взвешенные частицы жидкой фазы. Влажный насыщенный пар, насыщенный пар, в котором содержатся взвешенные частицы жидкой фазы. Степень сухости пара, массовая доля сухого пара во влажном насыщенном паре. Обозначают х. Степень сухости может изменяться от 0 до 1. При х = 0 – кипящая жидкость, при х = 1 - сухой насыщенный пар. Перегретый пар, пар, температура которого выше температуры кипения при одинаковом давлении.
Основные параметры воды, параметры, необходимые для проведения термодинамических расчетов: давление, температура, удельный объем, энтальпия, энтропия. Поскольку вода является реальным веществом, сведения о параметрах и функциях состояния получают экспериментальным путем, а затем представляют в виде таблиц, диаграмм (Ts-, hs -диаграммы) и уравнений состояния. Начало отсчета энтальпии и энтропии воды - состояние в тройной точке (h 0 = 0, s 0 = 0). Параметры, относящиеся к состоянию кипящей жидкости, обозначают индексом «'», например, v ', h ', s '. Параметры, относящиеся к состоянию сухого насыщенного пара, обозначают индексом «"», например, v ", h ", s ". Параметры влажного насыщенного пара определяют с помощью фазовых диаграмм, или рассчитывают по правилу аддитивности: v = v " x + v '(1 – x), h = h " x + h '(1 – x) = h ' + rx, s = s " x + s '(1 – x) = s ' + rx / Tн. При невысоких и средних давлениях (до 10 МПа), функции состояния можно определять расчетным путем (с достаточной для технических расчетов точностью). Необходимые формулы представлены в таблице, где cрж» 4,19 кДж/(кг×К) – изобарная теплоемкость жидкой воды; cрп - средняя изобарная теплоемкость перегретого пара в интервале температур от температуры кипения до данной температуры. Таблица – Расчет функций состояния воды
Процесс получения пара, процесс 1-2-3-4, представленный на рисунке и протекающий с подводом теплоты. В технических устройствах этот процесс рассматривают как изобарный, состоящий из трех частей: 1-2 - изобарный подогрев воды до температуры кипения; 2-3 - изобарно-изотермическое парообразование; 3-4 - изобарный перегрев пара. Обратный процесс (4-3-2-1) протекает с отводом теплоты и заключается в изобарном охлаждении перегретого пара до температуры кипения (4-3), изобарно-изотермической конденсации (3-2) и изобарном охлаждении жидкости ниже температуры кипения (2-1). Термодинамические процессы с водяным паром, изохорный, изобарный, изотермический и адиабатный процесс.
Изохорный процесс. Процесс 1-2 – подвод теплоты. Работа изменения объема: l = 0. Располагаемая работа: lp = v (p 1 – p 2).
|
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 1006; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.255.58 (0.015 с.) |

 ; работу располагаемую
; работу располагаемую  ; работу проталкивания
; работу проталкивания  .
. Идеальный газ, газ, в котором отсутствуют силы межмолекулярного взаимодействия, а объем молекул равен нулю. Реальный газ приближается к идеальному при низком давлении (до 2 МПа) и высокой температуре (более 20оС).
Идеальный газ, газ, в котором отсутствуют силы межмолекулярного взаимодействия, а объем молекул равен нулю. Реальный газ приближается к идеальному при низком давлении (до 2 МПа) и высокой температуре (более 20оС). . Здесь V m = 22,4 м3/кмоль – объем киломоля идеального газа.
. Здесь V m = 22,4 м3/кмоль – объем киломоля идеального газа. , где п – количество компонентов в смеси.
, где п – количество компонентов в смеси. , Дж/(кг×К).
, Дж/(кг×К).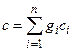 ,
,  ,
,  , где п – количество компонентов в смеси.
, где п – количество компонентов в смеси. ,
,  ,
,  ,
, ,
,  ,
,  .
. .
. , Дж, удельная энтальпия
, Дж, удельная энтальпия  , Дж/кг. Изменение энтальпии в процессе не зависит от пути его протекания, а определяется только начальным и конечным состояниями. Для идеального газа изменение энтальпии в процессе зависит только от температуры и определяется из выражения:
, Дж/кг. Изменение энтальпии в процессе не зависит от пути его протекания, а определяется только начальным и конечным состояниями. Для идеального газа изменение энтальпии в процессе зависит только от температуры и определяется из выражения:  .
.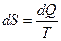 , Дж/К, удельная энтропия
, Дж/К, удельная энтропия  , Дж/кг. Поскольку Т > 0, то подвод теплоты в процессе (dq > 0) сопровождается увеличением энтропии (ds > 0), а отвод теплоты (dq < 0) сопровождается её уменьшением (ds < 0).
, Дж/кг. Поскольку Т > 0, то подвод теплоты в процессе (dq > 0) сопровождается увеличением энтропии (ds > 0), а отвод теплоты (dq < 0) сопровождается её уменьшением (ds < 0). Ts -диаграмма, диаграмма, в которой по оси абсцисс откладывают удельную энтропию, а по оси ординат абсолютную температуру. В диаграмме можно изображать равновесные процессы, например, 1-2 – процесс с подводом теплоты (ds > 0). Так как теплота, подведенная в процессе равна
Ts -диаграмма, диаграмма, в которой по оси абсцисс откладывают удельную энтропию, а по оси ординат абсолютную температуру. В диаграмме можно изображать равновесные процессы, например, 1-2 – процесс с подводом теплоты (ds > 0). Так как теплота, подведенная в процессе равна  , то площадь под процессом в Тs -диаграмме равна теплоте q.
, то площадь под процессом в Тs -диаграмме равна теплоте q. или
или  . Эти соотношения справедливы и для обратимых (знак равенства) и для необратимых (знак >) процессов в любой системе.
. Эти соотношения справедливы и для обратимых (знак равенства) и для необратимых (знак >) процессов в любой системе. , где q 2 – теплота, отводимая в цикле. Величина КПД всегда меньше единицы. Для увеличения КПД следует увеличивать q 1 и уменьшать q 2.
, где q 2 – теплота, отводимая в цикле. Величина КПД всегда меньше единицы. Для увеличения КПД следует увеличивать q 1 и уменьшать q 2. , где q 1 – теплота, отводимая в окружающую среду. Величина холодильного коэффициента больше единицы.
, где q 1 – теплота, отводимая в окружающую среду. Величина холодильного коэффициента больше единицы. Цикл Карно, цикл, состоящий из двух адиабатных и двух изотермических процессов. На рисунке изображен прямой обратимый цикл Карно 1-2-3-4-1. Процессы: 1-2 - адиабатное расширение рабочего тела; 2-3 - изотермический отвод теплоты; 3-4 - адиабатное сжатие; 4-1 - изотермический подвод теплоты. Величина термического КПД цикла Карно не зависит от свойств рабочего тела, а определяется только температурой подвода и отвода теплоты:
Цикл Карно, цикл, состоящий из двух адиабатных и двух изотермических процессов. На рисунке изображен прямой обратимый цикл Карно 1-2-3-4-1. Процессы: 1-2 - адиабатное расширение рабочего тела; 2-3 - изотермический отвод теплоты; 3-4 - адиабатное сжатие; 4-1 - изотермический подвод теплоты. Величина термического КПД цикла Карно не зависит от свойств рабочего тела, а определяется только температурой подвода и отвода теплоты:  . Цикл Карно имеет наибольший КПД по сравнению с любым другим циклом, осуществляемым в том же интервале температур. Цикл служит эталоном при оценке совершенства любых циклов тепловых машин.
. Цикл Карно имеет наибольший КПД по сравнению с любым другим циклом, осуществляемым в том же интервале температур. Цикл служит эталоном при оценке совершенства любых циклов тепловых машин. .
. (интеграл Клаузиуса) равен нулю:
(интеграл Клаузиуса) равен нулю:  . Для обратимого процесса
. Для обратимого процесса  . Если последнее выражение записать в виде
. Если последнее выражение записать в виде 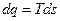 , то получим уравнение второго закона термодинамики для обратимых процессов.
, то получим уравнение второго закона термодинамики для обратимых процессов. . Для необратимого процесса
. Для необратимого процесса  . Это означает, что в необратимых процессах энтропия рабочего тела увеличивается по сравнению с обратимым процессом при одинаковом значении dq. Выражение
. Это означает, что в необратимых процессах энтропия рабочего тела увеличивается по сравнению с обратимым процессом при одинаковом значении dq. Выражение  является уравнением второго закона термодинамики для необратимых процессов.
является уравнением второго закона термодинамики для необратимых процессов. . Индексом «0» отмечены параметры рабочего тела при условиях окружающей среды, а u, s, v – параметры рабочего тела в рассматриваемом состоянии.
. Индексом «0» отмечены параметры рабочего тела при условиях окружающей среды, а u, s, v – параметры рабочего тела в рассматриваемом состоянии. .
. .
.
 ;
;  ;
;  ; lp = 0;
; lp = 0; 

 ;
;  ;
;  ;
;  ;
;  ;
; 

 , где k – показатель адиабаты. Для идеального газа
, где k – показатель адиабаты. Для идеального газа  и принимает следующие значения: для одноатомных газов k = 1,67, для двухатомных газов k = 1,4, для трёх- и многоатомных газов k = 1,29. Основные формулы для расчета адиабатного процесса с идеальным газом:
и принимает следующие значения: для одноатомных газов k = 1,67, для двухатомных газов k = 1,4, для трёх- и многоатомных газов k = 1,29. Основные формулы для расчета адиабатного процесса с идеальным газом: ;
;  ;
; ;
;  ; l = -D u; lp = -D h = h 1 – h 2
; l = -D u; lp = -D h = h 1 – h 2
 , где п – показатель политропы. Для идеального газа
, где п – показатель политропы. Для идеального газа  . Изохорный, изобарный, изотермический и адиабатный процесс являются частным случаем политропного процесса. Основные формулы для расчета политропного процесса с идеальным газом:
. Изохорный, изобарный, изотермический и адиабатный процесс являются частным случаем политропного процесса. Основные формулы для расчета политропного процесса с идеальным газом: ;
;  ;
;  ;
;  ;
; ;
;  ;
; 
 для идеальных газов равен единице, а для реальных газов имеет сложную зависимость от давления и температуры.
для идеальных газов равен единице, а для реальных газов имеет сложную зависимость от давления и температуры. , где a, b – константы, которые наряду с газовой постоянной характеризуют индивидуальные свойства вещества. Если сравнить это уравнение с уравнением Клапейрона pv = RT, то видно, что вместо р в нем фигурирует
, где a, b – константы, которые наряду с газовой постоянной характеризуют индивидуальные свойства вещества. Если сравнить это уравнение с уравнением Клапейрона pv = RT, то видно, что вместо р в нем фигурирует  , а вместо v стоит
, а вместо v стоит  . Согласно уравнению Клапейрона при стремлении давления к бесконечности удельный объем стремится к нулю, а из уравнения Ван-дер-Ваальса следует, что в этом случае v ® b. Следовательно, величину b можно интерпретировать как объем занимаемый собственно молекулами. Член
. Согласно уравнению Клапейрона при стремлении давления к бесконечности удельный объем стремится к нулю, а из уравнения Ван-дер-Ваальса следует, что в этом случае v ® b. Следовательно, величину b можно интерпретировать как объем занимаемый собственно молекулами. Член  учитывает взаимодействие молекул газа. Эту величину можно рассматривать как внутреннее давление в газе. Константы a и b могут быть вычислены через критические параметры вещества
учитывает взаимодействие молекул газа. Эту величину можно рассматривать как внутреннее давление в газе. Константы a и b могут быть вычислены через критические параметры вещества  ,
,  . В этих выражениях Ткр – критическая температура, ркр – критическое давление, vкр – критический удельный объем. Уравнение Ван-дер-Ваальса только качественно отражает поведение веществ и для точных расчетов не пригодно.
. В этих выражениях Ткр – критическая температура, ркр – критическое давление, vкр – критический удельный объем. Уравнение Ван-дер-Ваальса только качественно отражает поведение веществ и для точных расчетов не пригодно. Фазовая диаграмма, диаграмма, на которой нанесены линии фазовых переходов. На рисунке представлена фазовая диаграмма в координатах р, Т. Линия ОВ - кривая сублимации (десублимации) вещества, линия ОА - кривая плавления (затвердевания), линия ОК - кривая насыщения (кипения или конденсации). Точка О - тройная точка. Точка К - критическая точка.
Фазовая диаграмма, диаграмма, на которой нанесены линии фазовых переходов. На рисунке представлена фазовая диаграмма в координатах р, Т. Линия ОВ - кривая сублимации (десублимации) вещества, линия ОА - кривая плавления (затвердевания), линия ОК - кривая насыщения (кипения или конденсации). Точка О - тройная точка. Точка К - критическая точка.










