
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 2. Теория теплообменаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1 Основные понятия и определения
Теплообмен, самопроизвольный процесс переноса теплоты, возникающий под действием пространственной неоднородности поля температуры. Перенос теплоты может осуществляться тремя способами: теплопроводностью, конвекцией и излучением. Теплопроводность, перенос теплоты от более нагретых участков к менее нагретым в результате теплового движения и взаимодействия микрочастиц. Имеет место в твердых телах и неподвижных газах и жидкостях. Конвекция, перенос теплоты при перемещении объемов жидкости или газа в пространстве из области с одной температурой в область с другой температурой. Имеет место только в текучих средах. Конвективный перенос теплоты происходит тем интенсивнее, чем больше скорости движения жидкости или газа, так как в этом случае за единицу времени перемещается большее количество частиц тела. Перенос теплоты конвекцией всегда сопровождается теплопроводностью, так как при этом осуществляется и непосредственный контакт частиц с различной температурой. Одновременный перенос теплоты конвекцией и теплопроводностью называют конвективным теплообменом;он может быть вынужденным и свободным. Если движение рабочего тела вызвано искусственно (вентилятором, компрессором, мешалкой и др.), то такой конвективный теплообмен называют вынужденным. Если же движение рабочего тела возникает под влиянием разности плотностей отдельных частей жидкости в результате нагревания, то такой теплообмен называют свободным или естественным, конвективным теплообменом. Излучение, процесс передачи теплоты между двумя телами, разделенными полностью или частично пропускающей излучение средой, происходит в три стадии: превращение части внутренней энергии одного из тел в энергию электромагнитных волн, распространение электромагнитных волн в пространстве, поглощение энергии излучения другим телом. При сравнительно невысоких температурах перенос энергии осуществляется в основном инфракрасными лучами. Сложный теплообмен, совокупность всех трех видов переноса теплоты: теплопроводность, конвекция, излучение. Изучение закономерностей сложного теплообмена представляет собой довольно трудную задачу. Поэтому изучают порознь каждый из трех видов теплообмена, после чего становится возможным вести расчеты, относящиеся к сложному теплообмену.
Теплопроводность
Теплопроводность (кондукция) – процесс распространения теплоты при непосредственном соприкосновении отдельных частиц тела, имеющих различные температуры. Теплопроводность обусловлена движением микрочастиц тела. В газах перенос теплоты осуществляется путем диффузии молекул и атомов. В жидкостях и твердых телах - диэлектриках - путем упругих волн. В металлах перенос энергии в основном осуществляется путем диффузии свободных электронов, а роль упругих колебаний кристаллической решетки имеет второстепенное значение. Аналитическая теория теплопроводности рассматривает вещество как сплошную среду, игнорируя его молекулярное строение. Такой подход правомерен, если размеры объектов исследования значительно больше размеров молекул и расстояния между ними. Возникновение процесса переноса теплоты обусловлено наличием разности температур в различных точках тела (пространства). Совокупность значений температур во всех точках рассматриваемого пространства в данный момент времени называется температурным полем. Если температура зависит только от пространственных координат x, y, z, то такое поле называется стационарным t = f (x, y, z). Если температура зависит и от времени t, т. е. t = f (x, y, z, t), то температурное поле называется нестационарным. Наиболее простой вид имеет уравнение одномерного стационарного температурного поля: t = f (x).
Размерность градиента температуры К/м.
Количество теплоты, передаваемой через изотермическую поверхность F в единицу времени называют тепловым потоком Q. Единица измерения - Вт. Тепловой поток, отнесенный к площади F называют плотностью теплового потока q = Q / F. Размерность - Вт/м2. В основе теории теплопроводности лежит закон (гипотеза) Фурье, в соответствии с которым плотность теплового потока переданного теплопроводностью пропорциональна градиенту температуры:
Знак «минус» в правой части уравнения отображает противоположность направлений векторов теплового потока и температурного градиента: теплота передается в сторону понижения температуры (рисунок). Коэффициент пропорциональности l называется коэффициентом теплопроводности. Его физический смысл следует из выражения:
Как видно, коэффициент теплопроводности характеризует способность тел проводить теплоту, и численно равен плотности теплового потока переданного теплопроводностью при градиенте температуры равном единице. Следовательно, коэффициент теплопроводности зависит только от свойств и параметров состояния тела и является его теплофизической характеристикой. Коэффициент теплопроводности определяется экспериментальным путем и для инженерных расчетов выбирается из справочника. Величина коэффициента теплопроводности газов лежит в пределах от 0,006 до 0,6 Вт/(м×К). Его значение возрастает с повышением температуры и с уменьшением массы молекул. Для большинства газов теплопроводность слабо зависит от давления, исключение составляют очень маленькие и очень большие давления. Коэффициенты теплопроводности водяного пара и других реальных газов, существенно отличающихся от идеальных, сильно зависят от давления. Для газовых смесей l не может быть определен по закону аддитивности, его определяют опытным путем. Величина коэффициент теплопроводности капельных жидкостей лежит в пределах от 0,07 до 0,7 Вт/(м×К). Опыты показывают, что для большинства жидкостей с повышением температуры коэффициент теплопроводности уменьшается, исключение составляют вода и глицерин. Причем для воды, в зависимости от параметров состояния, теплопроводность может, как увеличиваться, так и уменьшаться. При повышении давления l жидкостей возрастает. В чистых металлах теплопроводность высокая, например, для серебра l = 450 Вт/(м×К). С повышением температуры коэффициент теплопроводности металлов уменьшается. При наличии в металлах примесей l резко убывает (это объясняется увеличением структурных неоднородностей, которые приводят к рассеиванию электронов), например, для чистой меди l = 396 Вт/(м×К), а для меди со следами мышьяка l = 142 Вт/(м×К). Для сплавов при повышении температуры l увеличивается. В диэлектриках с повышением температуры коэффициент теплопроводности обычно увеличивается. Он зависит также от структуры материала, его пористости и влажности. Многие строительные и теплоизоляционные материалы имеют пористое строение (кирпич, бетон, асбест и др.), поэтому для них коэффициент теплопроводности является условной величиной, учитывающей теплопроводность твердой структуры и среды, заполняющей поры. Такой коэффициент теплопроводности называется эффективным. Коэффициенты теплопроводности этих материалов имеют значения от 0,023 до 2,9 Вт/(м×К). Материалы с l < 0,25 Вт/(м×К), являются теплоизоляционными.
Дифференциальное уравнение теплопроводности, уравнение, устанавливающее соотношение между изменением температуры во времени и ее изменением в пространстве. В самом общем виде уравнение имеет вид
где a = l/(C ×r) – коэффициент температуропроводности, м2/с, характеризует теплоинерционные свойства вещества; C ×r – объемная теплоемкость тела, является мерой тепловой инерции тела;
qv – объемная плотность внутренних источников теплоты. Для стационарного одномерного температурного поля без внутренних тепловыделений дифференциальное уравнение примет вид:
Краевые условия. Поскольку дифференциальное уравнение теплопроводности относится к бесконечно малому элементу температурного поля, оно само по себе не отражает развитие процесса теплопроводности во всем рассматриваемом пространстве за весь период времени. Для получения полной картины процесса нужно зафиксировать условия однозначности в виде геометрических условий (форма и размеры тела), физических условий (значения коэффициентов тепло- и температуропроводности), а также задать краевые условия. В краевые условия входят временные условия (начальное распределение температуры в теле) и граничные условия, определяющие условия теплообмена на границах тела. Граничные условия бывают: 1) граничные условия первого рода, когда задаются распределением температур на поверхности тела в зависимости от координат и времени; 2) граничные условия второго рода, когда задаются распределением плотности теплового потока на поверхности тела в зависимости от координат и времени; 3) граничные условия третьего рода, когда задаются температурой среды, омывающей поверхность тела tж, и законом теплообмена между поверхностью и средой. В качестве этого закона используют закон Ньютона-Рихмана
где tc – температура стенки; a – коэффициент теплоотдачи, Вт/(м2×К). Коэффициент теплоотдачи характеризует интенсивность теплообмена между поверхностью тела и окружающей средой и численно равен плотности теплового потока переданного конвекцией при температурном напоре равном единице. Коэффициент теплоотдачи зависит от многих факторов, но при решении задач теплопроводности твердого тела его принимают в большинстве случаев величиной постоянной. 4) граничные условия четвертого рода соответствуют теплообмену поверхности тела со средой при равенстве их температур или теплообмену соприкасающихся твердых тел, когда температуры соприкасающихся поверхностей одинаковы.
Решение дифференциального уравнения теплопроводности при заданных условиях однозначности позволяет определить температурное поле во всем объеме тела для любого момента времени или найти функцию t = f (x, y, z, τ). Теплопроводность при стационарном режиме. Теплопроводность через плоскую однослойную стенку.
Для определения плотности теплового потока воспользуемся уравнением Фурье:
Теплопроводность через плоскую многослойную стенку.
Решая уравнения относительно разности температур, получим:
После суммирования этих выражений остается Теплопроводность через цилиндрическую однослойную стенку.
Разделим переменные Для определения постоянной интегрирования С используем граничные условия первого рода: при r = r 1, t = tc 1, тогда Теплопроводность через многослойную цилиндрическую стенку.
Решая эту систему относительно разности температур, получим:
После суммирования полученных уравнений можно записать:
Конвективный теплообмен Основные понятия. Конвекция, происходит только в газах и жидкостях и состоит в том, что перенос теплоты осуществляется перемещающимися в пространстве объемами среды. Передача теплоты конвекцией всегда связана с теплопроводностью. Совместный процесс конвекции и теплопроводности называется конвективным теплообменом.
Различают конвекцию вынужденную (движение жидкости создается искусственно) и свободную – движение возникает в связи с ее нагреванием и изменением плотности. О. Рейнольдс в 1884 г. в своих опытах установил, что при движении жидкости встречаются два вида потока, подчиняющихся различным законам. В потоке первого вида все частицы движутся только по параллельным между собой траекториям, и движение их длительно совпадает с направлением всего потока. Жидкость движется спокойно, без пульсаций, образуя струи, следующие очертаниям канала. Движение такого рода называется ламинарным. Второй вид потока называется турбулентным, в нем непрерывно происходит перемешивание всех слоев жидкости. Каждая частица потока, перемещаясь вдоль канала с некоторой скоростью, совершает различные движения перпендикулярно стенкам канала. В связи с этим поток представляет собой беспорядочную массу хаотически движущихся частиц. Чем больше образуется пульсаций, завихрений, тем больше турбулентность потока. При переходе ламинарного движения в турбулентное сопротивление от трения в канале возрастает. Характер движения жидкости влияет на интенсивность передачи теплоты. При ламинарном режиме и отсутствии естественной конвекции теплоты в перпендикулярном к стенке направлении передается только теплопроводностью. Количество этой теплоты зависит от физических свойств жидкости, геометрических размеров, формы поверхности канала и почти не зависит от скорости. При турбулентном движении жидкости перенос теплоты наряду с теплопроводностью осуществляется перпендикулярным к поверхности канала перемещением частиц. Факторы, влияющие на интенсивность конвективного теплообмена. Физические свойства жидкостей. В качестве жидких и газообразных теплоносителей в технике применяют различные вещества: воздух, воду, газы, масло, нефть, спирт, ртуть, расплавленные металлы и многие другие. В зависимости от физических свойств этих веществ процессы теплоотдачи протекают, различно. Большое влияние на теплообмен оказывают следующие физические параметры: коэффициент теплопроводности l,удельная теплоемкость с,плотность r, коэффициент температуропроводности а и коэффициент динамической вязкости m (или коэффициент кинематической вязкости n = m/r). Эти параметры для каждого вещества имеют определенные значения и являются функцией температуры, а некоторые из них и давления. Режимы течения и пограничный слой. Теоретическое рассмотрение задач конвективного теплообмена основывается на использовании теории пограничного слоя, данной Л. Прандтлем. Рассмотрим процесс продольного омывания какого-либо тела безграничным потоком жидкости с постоянной скоростью течения w. Вследствие влияния сил трения в непосредственной близости от поверхности тела скорость течения должна очень быстро падать до нуля. Тонкий слой жидкости вблизи поверхности тела, в котором происходит изменение скорости жидкости от значения скорости невозмущенного потока вдали от стенки до нуля непосредственно на стенке, называется динамическим пограничным слоем. Толщина этого слоя б возрастает вдоль по потоку. С увеличением скорости потока толщина динамического пограничного слоя уменьшается вследствие сдувания его потоком. Напротив, с увеличением вязкости толщина динамического слоя увеличивается. Течение в динамическом пограничном слое может быть как турбулентным, так и ламинарным (см. рисунок).
Если температуры стенки и жидкости неодинаковы, то вблизи стенки образуется тепловой пограничный слой,в котором происходит все изменение температуры жидкости. Вне пограничного слоя температура жидкости постоянна t 0. В общем случае толщины теплового и динамического слоев могут не совпадать. Соотношение толщин динамического и теплового пограничных слоев определяется величиной безразмерного числа Pr = n/ a. Для вязких жидкостей с низкой теплопроводностью (например, масел) Рг > 1 и толщина динамического пограничного слоя больше толщины теплового пограничного слоя. Для газов Рг» 1 и толщины слоев приблизительно одинаковы. Для жидких металлов Рг < 1 и тепловой пограничный слой проникает в область динамического невозмущенного потока. Механизм и интенсивность переноса теплоты зависят от характера движения жидкости в пограничном слое. Если движение внутри теплового пограничного слоя ламинарное, то теплота в направлении, перпендикулярном к стенке, переносится теплопроводностью. Однако у внешней границы слоя, где температура по нормали к стенке меняете незначительно, преобладает перенос теплоты конвекцией вдоль стенки.- При турбулентном течении в тепловом пограничном слое перенос теплоты в направлении к стенке в основном обусловлен турбулентным перемешиванием жидкости. Интенсивность такого переноса теплоты существенно выше интенсивности переноса теплоты теплопроводностью. Однако непосредственно у стенки, в ламинарном подслое, перенос теплоты к стенке осуществляется обычной теплопроводностью. Изменение физических свойств жидкости в пограничном слое зависит от температуры, в связи с чем интенсивность теплообмена между жидкостью и стенкой оказывается различной в условиях нагревания и охлаждения жидкости. Так, например, для капельных жидкостей интенсивность теплообмена при нагревании будет большей, чем при охлаждении, вследствие уменьшения пограничного слоя. Следовательно, теплоотдача зависит от направления теплового потока. Очень большое значение для теплообмена имеют форма и размер поверхностей; в зависимости от них может резко меняться характер движения жидкости и толщина пограничного слоя.
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 1986; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.104.41 (0.01 с.) |

 Геометрическое место точек тела имеющих одинаковую температуру называют изотермической поверхностью. Рассмотрим изотермические поверхности, отличающиеся температурой на D t (рисунок). В любом направлении, пересекающем эти поверхности, происходит изменение температуры. Однако наиболее интенсивно температура изменяется в направлении нормали к изотермической поверхности. Это возрастание температуры характеризуется градиентом температуры - вектором, направленным по нормали к изотермической поверхности в сторону возрастания температуры и численно равным производной от температуры по расстоянию, измеренному по нормали D n:
Геометрическое место точек тела имеющих одинаковую температуру называют изотермической поверхностью. Рассмотрим изотермические поверхности, отличающиеся температурой на D t (рисунок). В любом направлении, пересекающем эти поверхности, происходит изменение температуры. Однако наиболее интенсивно температура изменяется в направлении нормали к изотермической поверхности. Это возрастание температуры характеризуется градиентом температуры - вектором, направленным по нормали к изотермической поверхности в сторону возрастания температуры и численно равным производной от температуры по расстоянию, измеренному по нормали D n: .
. .
. , Вт/(м×К).
, Вт/(м×К). ,
, – оператор Лапласа, характеризует изменение температуры в пространстве;
– оператор Лапласа, характеризует изменение температуры в пространстве; .
. ,
, – температурный напор;
– температурный напор; Рассмотрим плоскую однослойную стенку с коэффициентом теплопроводности l и толщиной d. Пусть высота и ширина стенки гораздо больше толщины. Температурное поле в этом случае можно считать одномерным. Тогда дифференциальное уравнение теплопроводности при стационарном режиме имеет вид:
Рассмотрим плоскую однослойную стенку с коэффициентом теплопроводности l и толщиной d. Пусть высота и ширина стенки гораздо больше толщины. Температурное поле в этом случае можно считать одномерным. Тогда дифференциальное уравнение теплопроводности при стационарном режиме имеет вид:  . После двойного интегрирования получим:
. После двойного интегрирования получим:  . Для определения констант интегрирования воспользуемся граничными условиями первого рода: при x = 0, t = tc 1, следовательно, С 2 = tc 1. При x = d, t = tc 2, следовательно,
. Для определения констант интегрирования воспользуемся граничными условиями первого рода: при x = 0, t = tc 1, следовательно, С 2 = tc 1. При x = d, t = tc 2, следовательно,  . Подставляя константы интегрирования, получим уравнение температурного поля:
. Подставляя константы интегрирования, получим уравнение температурного поля: .
.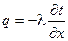 , которое можно переписать в виде
, которое можно переписать в виде  . В результате интегрирования получим:
. В результате интегрирования получим:  . Константы интегрирования можно определить, воспользовавшись граничными условиями первого рода: при x = 0, t = tc 1, следовательно, С = tc 1. При x = d, t = tc 2, следовательно
. Константы интегрирования можно определить, воспользовавшись граничными условиями первого рода: при x = 0, t = tc 1, следовательно, С = tc 1. При x = d, t = tc 2, следовательно  и окончательно получим
и окончательно получим .
. Рассмотрим п -слойную плоскую стенку при условии одномерного температурного поля. При стационарном режиме плотность теплового потока прошедшего через каждый слой этой стенки будет одинакова. Тогда для каждого слоя можно записать уравнение теплопроводности:
Рассмотрим п -слойную плоскую стенку при условии одномерного температурного поля. При стационарном режиме плотность теплового потока прошедшего через каждый слой этой стенки будет одинакова. Тогда для каждого слоя можно записать уравнение теплопроводности: ,
,  , …,
, …,  .
. ,
,  , …,
, …, 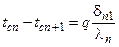 .
. , отсюда окончательно получим выражение для плотности теплового потока
, отсюда окончательно получим выражение для плотности теплового потока  .
. Рассмотрим однослойную цилиндрическую стенку длина которой l значительно больше внешнего диаметра (l >> 2 r 2). В этом случае тепловой поток можно считать одномерным. Выделим кольцевой слой радиусом r и толщиной dr. Для этого слоя в соответствии с законом Фурье можно записать
Рассмотрим однослойную цилиндрическую стенку длина которой l значительно больше внешнего диаметра (l >> 2 r 2). В этом случае тепловой поток можно считать одномерным. Выделим кольцевой слой радиусом r и толщиной dr. Для этого слоя в соответствии с законом Фурье можно записать .
. и проинтегрируем. После интегрирования получим
и проинтегрируем. После интегрирования получим  .
. ; при r = r 2, t = tc 2, тогда
; при r = r 2, t = tc 2, тогда  . Разность этих выражений дает
. Разность этих выражений дает  , или, решая относительно теплового потока окончательно получим
, или, решая относительно теплового потока окончательно получим  .
. При стационарной теплопроводности через многослойную цилиндрическую стенку тепловой поток через каждый слой будет одинаков, тогда можно записать для каждого слоя:
При стационарной теплопроводности через многослойную цилиндрическую стенку тепловой поток через каждый слой будет одинаков, тогда можно записать для каждого слоя: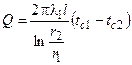 ,
,  ,…,
,…,  .
. ,
,  ,…,
,…, 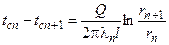 .
. , отсюда
, отсюда  .
. Необходимо отметить, что в случае турбулентного динамического пограничного слоя непосредственно у стенки имеется очень тонкий слой жидкости, движение в котором имеет ламинарный характер. Этот слой называют вязким или ламинарным подслоем.
Необходимо отметить, что в случае турбулентного динамического пограничного слоя непосредственно у стенки имеется очень тонкий слой жидкости, движение в котором имеет ламинарный характер. Этот слой называют вязким или ламинарным подслоем.


