
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет теплообменных аппаратовСодержание книги
Поиск на нашем сайте
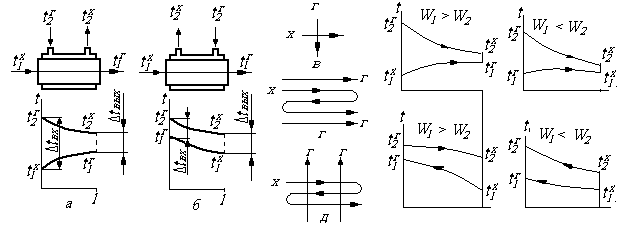
Теплообменный аппарат (теплообменник) – это устройство, предназначенное для нагревания, охлаждения или изменения агрегатного состояния теплоносителя путем теплообмена между двумя теплоносителями. По принципу действия теплообменники подразделяются на три основные группы: рекуперативные; регенеративные; смесительные. К теплообменникам относятся паровые котлы, печи, водо- и воздухоподогреватели, конденсаторы и т.п. Наиболее распространенным типом теплообменников являются трубчатые рекуперативные теплообменники, который представляет собой систему труб, в которых движется один теплоноситель, а снаружи перемещается другой теплоноситель. Следовательно, теплоносители разделены перегородкой и не контактируют друг с другом. Различают следующие основные схемы движения теплоносителей (рис. 9.3). На практике встречаются более сложные схемы движения теплоносителей, включающие различные комбинации основных схем. В регенеративных теплообменниках поверхность нагрева периодически омывается то горячим, то холодным теплоносителем. В смесительных теплообменниках теплота от одного теплоносителя к другому передается в результате смешения теплоносителей.
Рис. 9.3. Направление движения и графики изменения температур в рекуперативных теплообменниках: а – прямоточные (теплоносители движутся в одном направлении); б – противоточные (теплоносители движутся в противоположном направлении); в – перекрестные (теплоносители движутся во взаимно перпендикулярных направлениях); г, д – многократный перекрестный ток
При расчете теплообменных аппаратов используют следующие уравнения: • уравнение теплопередачи Q = к · F · (t1 – t2). (9.14) • уравнение теплового баланса Q = mгcpг(t1г – t2г) = mхcpх(t2х – t1х), (9.15) где mг, mх, cpг, cpх – массовые расходы и средние изобарные теплоемкости горячего и холодного теплоносителей; t1г и t2г, t2х и t1х – соответственно температуры горячего и холодного теплоносителей на входе и на выходе. Преобразуем уравнение (9.15) к виду: mгcpг/mхcpх = (t2х – t1х)/(t1г – – t2г) = W1/W2. Таким образом, W1/W2 = ∆tх/∆tг = ∆tвых/∆tвх, (9.16) где W = mcp – полная расходная теплоемкость (водяной эквивалент). Из формулы (9.16) следует, что изменение температуры однофазных теплоносителей обратно пропорционально их водяным эквивалентам. Площадь теплопередающей поверхности определяется при совместном решении уравнений (9.14) и (9.15): F = Q/(к∆t) = mгcpг(t1г – t2г) /(к∆t), (9.17) где к – коэффициент теплопередачи через поверхность. Входящие в зависимость к и ∆t изменяются по длине теплообменника, поэтому к определяют для средних температур теплоносителей, т.е. Изменения температур в наиболее простых случаях показано на рис. 9.3 при соотношениях расходных теплоемкостей W1 > W2 и Большие изменения температуры Δt = t1 – t2 характерны для теплоносителя с меньшим W. Температурный напор при прямотоке Δt изменяется сильнее, и среднее его значение меньше, чем при противотоке. Как следует из (9.17), поверхность противоточного теплообменника получается меньше, чем прямоточного. Соответственно уменьшаются его габариты и вес. Среднее значение
где ∆tб и ∆tм – большая и меньшая разность температур теплоносителей на входе и выходе теплообменника. Эта формула справедлива для любых схем движения теплоносителей. При отношении Dtб/Dtм <= 1,4 для определения Следует заметить, что среднелогарифмический напор всегда меньше среднеарифметического: Примеры решения задач Задача 1. Определить плотность излучения абсолютно черного тела, абсолютная температура которого равна 1500 К. Решение. Для определения спектральной плотности воспользуемся законом Стефана – Больцмана (9.6): Е0 = С0(Т/100)4. После подстановки в формулу (9.6) численных значений входящих в нее величин получим Е0 = 5,6686(1500/100)4 ≈ 287 кВт/м2. Задача 2. Какое количество тепла отводится излучением с оштукатуренной стены площадью 36 м2 к параллельной ей стене, покрытой деревом. Температура стенок 30 и 20°С соответственно. Среда, разделяющая стенки, заполнена одно- и двухатомными газами. Решение. Тепловой поток определяем по формуле (9.10) Q1–2 = c1–2S[(T1/100)4 – (T2/100)4]. В этой зависимости необходимо определить приведенный коэффициент излучения по формуле (9.11)
По таблице 14.1 [6, с. 340] с1 = 0,9 – степень черноты известковой штукатурки; с2 = 0,95 – степень черноты дерева. Таким образом,
Q1–2 = 4,9 · 36[(303,15/100)4 – (293,15/100)4] = 1877 Вт. Задача 3. Для условий задачи 2 определить, как изменится поток излучения от поверхности 1 к поверхности 2, если между поверхностями установлены 2 экрана. Решение. При отсутствии экранов тепловой поток получен в задаче 2 и равен Q1–2 = 1877 Вт. При установке 2 экранов поток определится по формуле Q(1–2)э = Q1–2/(n + 1) = 1877/(2 + 1) = 626 Вт.
|
||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 308; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.157.231 (0.007 с.) |

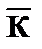 и
и 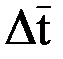 .
.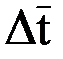 определяется среднелогарифмическим температурным напором:
определяется среднелогарифмическим температурным напором: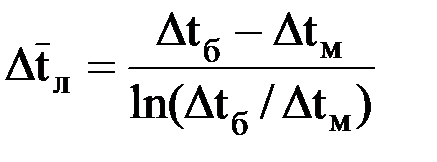 , (9.18)
, (9.18)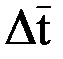 можно использовать зависимость
можно использовать зависимость 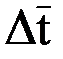 а = 0,5(∆tб + ∆tм), при этом ошибка составляет не более 4%; что допустимо для технических расчетов.
а = 0,5(∆tб + ∆tм), при этом ошибка составляет не более 4%; что допустимо для технических расчетов.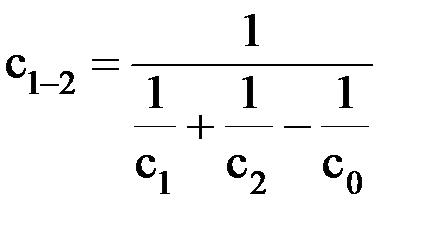 .
.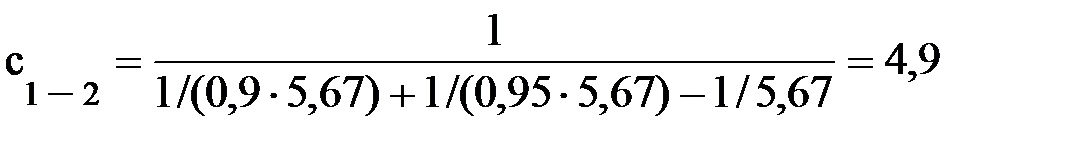 Вт/(м2·К4).
Вт/(м2·К4).


