
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование термодинамических процессовСодержание книги
Поиск на нашем сайте
Состояние газа можно изменить двумя путями: сообщить ему или отвести от него теплоту, путем сжатия или расширения. При этом важно знать, как в том или ином процессе распределяется теплота между внутренней энергией и работой, а также каково изменение параметров. Анализ процессов необходимо проводить в следующей последовательности: 1. Записать характерную особенность процесса. 2. Вывести уравнение процесса. 3. Установить связь между термодинамическими параметрами. 4. Изобразить процесс графически в координатах pv и Ts. 5. Определить теплоту, изменение внутренней энергии, энтальпии, энтропии, работу и теплоемкость. 6. Определить долю теплоты, которая расходуется на увеличение внутренней энергии и долю теплоты, которая идет на совершение внешней работы. Изменение внутренней энергии для всех процессов определяется по формуле du = cνdT, а энтальпии – dh = cpdT. Изохорный процесс
1. Характерной особенностью процесса является то, что он осуществляется при постоянном объеме, т.е. ν = const. 2. Уравнение состояния процесса получим из уравнения состояния идеального газа (1.8): p/T = const. 3. Таким образом, между давлением и температурой в изохорном процессе существует прямо пропорциональная зависимость: p2/p1 = = T2/T1. 4. Графическое изображение изохорного процесса в pv и Ts диаграммах представлено на рис. 3.1. 5. Определение теплоты и изменения энтропии процесса: – теплоту, подводимую к системе, определим, используя математическую формулировку первого закона термодинамики (2.5) dq = du + + pdν. В изохорном процессе dν = 0, поэтому dq = du; – в изохорном процессе отношение ν2/ν1 = 1, поэтому уравнение (2.30) принимает вид s2 – s1 = cνln(T2/T1), или в дифференциальной форме ds = cνdT/T. (3.1)
Рис. 3.1. Изображение изохорного процесса в pν- и Ts-диаграммах
6. В изохорном процессе объем не изменяется и работа равна нулю. 7. Теплоемкость изохорного процесса принято обозначать сν. 8. Доля теплоты, расходуемая на увеличение внутренней энергии, определяется по формуле α = du/δq, т.к. в изохорном процессе dq = du, получим α = 1, т.е. вся подведенная к термодинамической системе теплота идет на изменение внутренней энергии. Долю теплоты, которая идет на совершение внешней работы, можно определить по формуле α' = δl/δq = 1 – α. Учитывая, что α = 1, получим α' = 0. Изобарный процесс
1. Характерной особенностью процесса является то, что он осуществляется при постоянном давлении, т.е. p = const. 2. Уравнение состояния процесса получим из уравнения состояния идеального газа (1.8): ν/T = const. 3. Таким образом, между объемом и температурой в изобарном процессе существует прямо пропорциональная зависимость: ν2/ν1 = = T2/T1. 4. Графическое изображение изобарного процесса в pν- и Ts-диаграммах показано на рис. 3.2. 5. Определение теплоты и изменения энтропии процесса: – теплоту определим из уравнения (2.24): Δq = dh – νdp. В изобарном процессе dp = 0, поэтому вся подвденная теплота идет только на изменение энтальпии: δq = dh;
Рис. 3.2. Изображение изобарного процесса в рv- и Ts-диаграммах
– в изобарном процессе p2/p1 = 1, поэтому уравнение (2.31) в дифференциальной форме принимает вид ds = cpdT/T. 6. Работа процесса определяется интегрированием выражения dl = pdν в пределах от ν1 до ν2: l = p(ν2 – ν1). (3.2) 7. Теплоемкость изобарического процесса обозначают cp. 8. Доля теплоты, которая расходуется на увеличение внутренней энергии: α = 1/к, доля теплоты, которая идет на выполнение внешней работы: α' = 1 – 1/к = (к – 1)/к. Изотермический процесс
1. Характерная особенность процесса: T = const. 2. Уравнение состояния процесса: pν = const. 3. Связь между объемом и давлением имеет вид: ν2/ν1 = p1/p2.
Рис. 3.3. Изображение изотермического процесса в рv- и Ts-диаграммах
4. Графическое изображение изотермического процесса в pν- и Ts-диаграммах представлено на рис. 3.3. 5. Определение теплоты и изменения энтропии процесса: – теплота процесса равна работе: δq = δl = pdν; – из уравнений (2.30) и (2.31): учитывая, что T2/T1 = 1, s2 – s1 = = Rln(ν2/ν1) = –Rln(p2/p1) или в дифференциальной форме: ds = Rlnν = –Rlnp. (3.3) 6. Работу изотермического процесса определяют по формуле L = RTln(ν2/ν1) = RTln(p1/p2). (3.4) 7. Теплоемкость изотермического процесса равна ¥. 8. Доля теплоты, которая расходуется на увеличение внутренней энергии: α = du/δq = 0/δq = 0, доля теплоты, которая идет на выполнение внешней работы: α' = 1 – 0 = 1. Таким образом, вся подведенная в изотермическом процессе теплота идет на выполнение работы. Адиабатный процесс 1. Характерной особенностью процесса является то, что он осуществляется при отсутствии теплообмена системы с внешней средой: δq = 0. 2. Уравнение состояния процесса: pvк = const. (3.5) 3. Связь между давлением и объемом: p1ν1к = р2ν2к, или р2/р1 = (ν1/ν2)к. (3.6) Связь между температурой и объемом: Т2/Т1 = (ν1/ν2)к–1. (3.7) Связь между давлением и температурой:
4. Графическое изображение адиабатного процесса в рν- и Ts-диаграммах представлено на рис. 3.4.
Рис. 3.4. Изображение адиабатного процесса в рv- и Ts-диаграммах
5. Определение теплоты и изменения энтропии процесса: – из характеристики адиабатного процесса: δq = 0; – изменение энтропии системы: ds = 0. (3.9) 6. Работа адиабатного процесса определяется по одной из формул: l = (p1ν1 – p2ν2)/(к – 1); l = RT1[1 – p2/p1)(к – 1)/к/(к – 1). (3.10) 7. Теплоемкость адиабатного процесса равна нулю. 8. Доля теплоты, которая расходуется на увеличение внутренней энергии: α = du/0 = ∞, долю теплоты, которая идет на выполнение внешней работы: α' = 1 – ∞ = –∞. Политропный процесс
1. Характерной особенностью процесса является то, что он осуществляется при постоянной теплоемкости с и постоянном показателе политропы n. 2. Уравнение состояния процесса: Pνn = const. (3.11) 3. Связь между давлением и объемом: p1ν1n = р2ν2n, или р2/р1 = (ν1/ν2)n. (3.12) Связь между температурой и объемом: Т2/Т1 = (ν1/ν2)(n – 1)/n. (3.13) Связь между давлением и температурой: Т2/Т1 = (p2/p1)n – 1. (3.14) В формулах (3.11)–(3.14) n = (c – cp)/(c – cν) – показатель политропы. Из уравнения политропного процесса, задавая показателю политропы значения, получим: n = 0, p = const – изобарный процесс; n = 1, pν = const – изотермический процесс; n = к, pνк = const – адиабатный процесс; n = ∞, ν = const – изохорный процесс. 4. Графическое изображение политропного процесса в pν- и
Рис. 3.5. Изображение политропных процессов в рv- и Ts-диаграммах 5. Определение теплоты и изменения энтропии процесса: – теплота в политропном процессе: ∆q = cν(n – к)dT/(n – 1); – изменение энтропии системы: ds = cdT/T. (3.15) 6. Работа политропного процесса (но вместо показателя адиабаты к необходимо подставлять показатель политропы n): l = (p1ν1 – p2ν2)/(n – 1); l = RT1[1 – p2/p1)(n – 1)/n/(n – 1). (3.16) 7. Теплоемкость политропного процесса: с = сν(n – к)/(n – 1). (3.17) Анализ уравнения (3.17) показывает, что в диапазоне 1 < n < ктеплоемкость отрицательна, при этом δQ и dT имеют разные знаки. Работа совершается при подводе теплоты по всем политропам диапазона, кроме адиабаты, т.е. изменение теплоты положительно. Температура рабочего тела в процессе расширения понижается и, таким образом, изменение температуры является отрицательной величиной. 8. Доля теплоты, которая расходуется на увеличение внутренней энергии: α = (n – 1)/(n – к), а доля теплоты, которая идет на выполнение внешней работы: α' = (1 – к)/(n – к). Примеры решения задач Задача 1. В изобарном процессе к термодинамической системе, рабочим телом в которой является СО2, подводится теплота в количестве q = 50 кДж/кг. Определить количество теплоты, расходуемое на выполнение работы и на изменение внутренней энергии. Решение. Доля теплоты, расходуемой на изменение внутренней энергии, в изобарном процессе определяется по формуле α = 1/к. Для трех и более атомных газов показатель адиабаты к = 1,29. Следовательно, доля теплоты на изменение внутренней энергии составит Задача 2. В закрытом сосуде емкостью 0,5 м3 содержится азот при абсолютном давлении 0,5 МПа и температуре 15ºС. Определить абсолютное давление и температуру в сосуде после подвода к азоту 750 кДж тепла. Теплоемкость азота постоянна. Решение. Процесс изохорный. Массу азота в сосуде определяем по формуле m = p1V/RT1. Молярная масса азота равна 28, получим RN2 = 8314/28 Дж/(кг·К). После подстановки в формулу для определения m численных значений входящий в нее величин получим m = 0,5 х Определяем абсолютное давление в конце процесса: р2 = Т2 · р1/Т1 = 632 · 0,5/288 = 1,1 МПа. Второй закон термодинамики
|
||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 1350; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.216.248 (0.008 с.) |




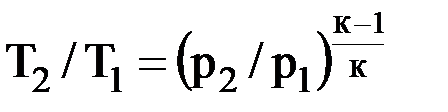 . (3.8)
. (3.8)




