
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Введение в техническую термодинамикуСодержание книги
Поиск на нашем сайте
Керученко, Л.С. К88 Теплофизика: учеб. пособие / Л.С. Керученко. – Омск: Изд-во ФГБОУ ВПО ОмГАУ им. П.А. Столыпина, 2014. – 148 с.: ил. ISBN 978-5-89764-372-1 Пособие написано в соответствии с требованиями ФГОС ВПО по направлению подготовки 280700– Техносферная безопасность (2009) и на основе авторской программы дисциплины «Теплофизика» (2010). Изложены основные положения теории тепловых процессов, освещены вопросы безопасности и защиты человека от техногенных и антропогенных воздействий, вызванных использованием теплоты. Издание предназначено для студентов высших учебных заведений, обучающихся по направлению подготовки бакалавров «Техносферная безопасность».
УДК 621.1 ББК 31.31
ISBN 978-5-89764-372-1 © Керученко Л.С., 2014 © ФГБОУ ВПО ОмГАУ им. П.А. Столыпина, 2014 © Оформление. Издательство ФГБОУ ВПО ОмГАУ им. П.А. Столыпина, 2014 Оглавление
Предисловие.................................................................................................. 6 Введение......................................................................................................... 8 1. Введение в термодинамику....................................................................... 9 1.1. Основные понятия и определения.................................................. 9 1.2. Параметры состояния рабочего тела............................................. 10 1.3. Уравнение состояния идеальных газов.......................................... 13 1.4. Уравнение состояния реальных газов............................................ 14 1.5. Газовые смеси.................................................................................. 15 1.6. Термодинамический процесс.......................................................... 16 1.7. Примеры решения задач................................................................ 17 2. Первый закон термодинамики для закрытых систем.............................. 20 2.1. Внутренняя энергия системы.......................................................... 20 2.2. Работа расширения, сжатия........................................................... 21 2.3. Уравнение первого закона термодинамики................................... 22 2.4. Теплоемкость рабочего тела.......................................................... 23 2.5. Энтальпия........................................................................................ 24 2.6. Энтропия......................................................................................... 25 2.7. Примеры решения задач................................................................ 26 3. Исследование термодинамических процессов......................................... 27 3.1. Изохорный процесс........................................................................ 27 3.2. Изобарный процесс........................................................................ 28 3.3. Изотермический процесс................................................................ 29 3.4. Адиабатный процесс....................................................................... 30 3.5. Политропный процесс.................................................................... 31 3.6. Примеры решения задач................................................................ 32 4. Второй закон термодинамики................................................................... 34 4.1. Круговые процессы, или циклы..................................................... 34 4.2. Цикл Карно..................................................................................... 35 4.3. Основные формулировки 2-го закона термодинамики................. 37 4.4. Изменение энтропии в обратимых и необратимых циклах.......... 38 4.5. Эксергия.......................................................................................... 40 4.6. Примеры решения задач................................................................ 42 5. Циклы поршневых двигателей внутреннего сгорания и воздушных компрессоров........................................................................................................................ 45 5.1. Циклы поршневых двигателей внутреннего сгорания.................. 45 5.2. Теоретический цикл поршневого компрессора............................. 47 5.3. Теоретический цикл многоступенчатого компрессора................. 48 5.4. Примеры решения задач................................................................ 49 6. Водяной пар и его свойства...................................................................... 52 6.1. Основные понятия и определения.................................................. 52 6.2. Процесс парообразования в pV-диаграмме.................................. 53 6.3. Изображение процесса парообразования в Ts-диаграмме........... 54 6.4. hs-диаграмма водяного пара.......................................................... 56 6.5. Основные параметры воды и водяного пара................................ 57 6.6. Процессы изменения состояния водяного пара в pV-, Ts- и hs-диаграммах........................................................................................................................ 60 6.7. Примеры решения задач................................................................ 63 7. Термодинамика потока............................................................................. 70 7.1. Уравнение первого закона термодинамики для потока................ 70 7.2. Истечение газов и паров................................................................. 71 7.3. Дросселирование газов и паров..................................................... 75 7.4. Примеры решения задач................................................................ 77 8. Основы теории теплообмена..................................................................... 79 8.1. Основные понятия........................................................................... 79 8.2. Теплопроводность.......................................................................... 80 8.3. Конвективный теплообмен............................................................. 83 8.4. Теплопередача................................................................................ 85 8.5. Тепловая изоляция.......................................................................... 87 8.6. Дифференциальное уравнение теплопроводности........................ 88 8.7. Дифференциальное уравнение конвективного теплообмена........ 89 8.8. Основные критерии подобия, используемые в теплотехнике....... 90 8.9. Массообмен..................................................................................... 94 8.10. Критерии подобия конвективного массообмена......................... 95 8.11. Примеры решения задач.............................................................. 95 9. Теплообмен излучением............................................................................ 98 9.1. Основные понятия и определения.................................................. 98 9.2. Основные законы теплообмена излучением.................................. 99 9.3. Определение теплообмена излучением.......................................... 101 9.4. Расчет теплообменных аппаратов.................................................. 102 9.5. Примеры решения задач................................................................ 105 Заключение.................................................................................................... 143 Библиографический список........................................................................... 144 Предметный указатель.................................................................................. 146
ПРЕДИСЛОВИЕ Дисциплину "Теплофизика" изучают студенты, обучающиеся по направлению подготовки 280700.62 - Техносферная безопасность в будущей практической деятельности которых вопросы, связанные с предотвращением и ликвидацией наиболее распространенных чрезвычайных ситуаций техносферного характера пожаров и взрывов занимают значительное место. Уже в студенческой аудитории они должны быть ориентированы на выявление причин возникновения пожаров и взрывов, разработку технических решений на их предотвращение, изучение поведения строительных конструкций в условиях пожара и обоснованию требований к их огнестойкости. За последние годы учебная литература практически не издавалась и, поэтому, ощущается необходимость в учебном пособии, которое соответствовало бы основным требованиям ФГОС ВПО по направлению подготовки «Техносферная безопасность». Высказанные соображения послужили основой для создания учебного пособия. Представленный в нем материал основан на теоретических разработках известных ученых в области термодинамики и тепломассообмена. Цель разработки данного пособия заключается в том, чтобы дать студентам основные представления о процессах тепломассообмена, проходящих в условиях возникновения и протекания пожаров и взрывов, происходящих на различных промышленных и сельскохозяйственных объектах; помочь студентам рационально организовать самостоятельную работу и лучше усвоить основные законы термодинамики и тепломассообмена для предотвращения техногенных катастроф, поэтому в нем отражены только ключевые моменты. Рассмотрение остального материала изучаемой дисциплины отводится на самостоятельную подготовку. После изучения представленного материала студент имеет возможность более углубленного изучения разделов теплофизики по первоисточникам. Для углубления знаний и детального знакомства с новинками в представленной области целесообразны знакомство с периодическими изданиями, посещение конференций различных уровней и ежегодных международных выставок, проводимых на территории ФГБОУ ВПО ОмГАУ им. П.А. Столыпина.
Пособие соответствует требованиям ФГОС ВПО (2009г.) и авторской программе по дисциплине Теплофизика» (2010г). Предназначено для студентов очной и заочной форм обучения направления подготовки 280700.62 - Техносферная безопасность, разработано с ориентацией на творческое изучение студентами проблем повышения эффективности решения задач, стоящих перед специалистами, работающими в области техносферной безопасности. По каждой теме приведены примеры решения задач, которые позволяют студентам самостоятельно углубиться в изучение темы. Автор учебного пособия канд. техн. наук, профессор кафедры агроинженерии ФГБОУ ВПО ОмГАУ им. П.А.Столыпина Керученко Леонид Степанович Автор признателен всем, кто выскажет свои замечания и пожелания по совершенствованию учебного пособия и преподавания дисциплины «Теплофизика». Замечания и предложения просим направлять по адресу: 644008 г. Омск, ФГБОУ ВПО ОмГАУ им. П.А. Столыпина, ул. Физкультурная, д. 1 (3-й уч. корпус), а также на E-mail: omgau.shmimzh@mail. Ru
ВВЕДЕНИЕ
Теплофизика – это наука, включающая совокупность дисциплин, представляющих теоретические основы энергетики. Она включает термодинамику, тепломассообмен, методы экспериментального и теоретического исследования равновесных и неравновесных свойств и веществ и тепловых процессов. Вопросы, изучаемые в теплофизике, имеют большое практическое значение при обеспечении охраны природной среды, особенно для предупреждения и тушения пожаров. Так, основные уравнения термодинамики используют при изучении работы двигателей внутреннего сгорания пожарных автомобилей и мотопомп, различных компрессоров, определения при пожаре количества оставшегося кислорода в изолирующем противогазе, а также при решении различных задач, связанных с противопожарной безопасностью. Законы тепломассообмена используются для расчета процессов возникновения и возможности продолжения пожара, скорости распространения пламени. При обучении бакалавров и подготовке их для работы в отрасли техносферной безопасности необходимо, прежде всего, знание основных закономерностей получения, переноса и использования теплоты, умение предупреждать процессы, приводящие к техносферным катастрофам и создание наиболее совершенных технологий отопления, вентиляции, хранения и переработки продукции, обеспечивающих безопасность людей и производства. Теплофизика как наука начала формироваться в середине XIX в. Значительная роль в становлении теплофизики принадлежит русским ученым, инженерам и изобретателям. Так, М.В. Ломоносов одним из первых высказал идею закона сохранения энергии. Данный закон после публикации работ Майера, Гельмгольца и экспериментального подтверждения Джоулем получил всеобщее признание. Д.И. Менделеев исследуя свойства газов установил для всех идеальных газов уравнение состояния. В.И. Гриневецкий, К.Э. Циолковский, А.А. Радциг и другие своими теоретическими и инженерными разработками создали основы проектирования целого ряда тепловых установок (котлы, тепловые двигатели, ракетные двигатели и т.д.). Особую роль в развитии теплофизике сыграли также труды иностранных ученых – Сади Карно, Нернста, Л. Больцмана, У. Гиббса, Ж. Гюи, А. Стодолы, Р. Ранта. Бакалавру, работающему в различных отраслях АПК, необходимо, в первую очередь, ясное понимание основ теплообмена, но этого невозможно добиться без использования знаний, полученных при изучении математики, физики и других дисциплин. Полученные в результате изучения дисциплины «Теплофизика» знания будут использованы при изучении таких дисциплин, как «Теория горения и взрыва», «Надежность технических систем и техногенный риск», «Безопасность жизнедеятельности», «Электроника и электротехника», «Медикобиологические основы безопасности» а также в практической работе при эксплуатации различных устройств, используемых для охраны природной среды и ресурсосбережении.
Газовые смеси Для получения тепла и рабочего тела в теплоэнергетических установках используют реакцию окисления топлива. Состав образующихся газовых смесей зависит от углеводородного состава топлива и условий его сгорания. Идеальной газовой смесью называется смесь идеальных газов, химически не взаимодействующих друг с другом. Для идеальной газовой смеси справедливо уравнение состояния (1.7), которое можно записать в виде рсм · νсм = Rсм · Тсм. (1.14) Каждый из газов, входящих в смесь, подчиняется своему уравнению рк · νк = Rк · Тк. (1.15) Для идеальной газовой смеси справедливы следующие предположения: 1. Закон Дальтона: где рсм – давление смеси; рк – парциальное давление к-го компонента смеси, т.е. давление, которое он имел бы при температуре смеси, если бы сам занимал объем, занимаемый смесью. 2. При равновесном состоянии газовой смеси каждый газ, входящий в состав газовой смеси, имеет температуру, равную температуре смеси. 3. Каждый газ распространяется по всему объему, занимаемому смесью, и поэтому объем каждого из газов равен объему смеси. Расчеты газовых смесей с использованием уравнения состояния (1.14) требуют предварительного вычисления газовых постоянных и молекулярных масс смесей. Состав газовых смесей задается весами, объемами или молями отдельных компонентов или массовыми или объемными долями. Массовая доля компонента смеси – это отношение массы данного компонента к массе смеси: gк = mк/mсм, (1.17) где mк – масса к-го компонента; Сумма массовых долей смеси равна 1. Газовая постоянная смеси определяется по формуле
где Rк – газовая постоянная к-го компонента смеси. Объемная доля к-го компонента смеси – это отношение парциального объема данного компонента к объему смеси. Парциальный объем – это объем, который занимал бы данный газ при давлении и температуре смеси. Математически объемная доля определяется следующим образом: rк = Vк/Vсм = Мк/Мсм, (1.19) где rк – объемная доля к-го компонента смеси; Vк – парциальный объем к-го компонента смеси; Vсм – объем смеси; Мк – число молей данного газа; Мсм = М1 + М2 + … + Мк + … + Мn – молярная масса смеси. Сумма объемных долей компонентов смеси равна единице, т.е. Массовая доля через объемную долю выражается уравнением
где rк – молярная доля компонента смеси. Численное значение парциальных давлений компонентов определяется по зависимости рк = rк · рсм. (1.21) Плотность смеси рассчитывается по формуле
Термодинамический процесс
Если параметры состояния во всех точках системы с течением времени не меняются, то состояние системы называется стационарным или равновесным, т.е. система находится в термодинамическом равновесии с окружающей средой.
Рис. 1.2. Обратимый термодинамический процесс Классическая термодинамика описывает только равновесные состояния и переходы из одного равновесного состояния в другое. Переход системы из одного равновесного состояния в другое равновесное состояние под воздействием внешней среды называют термодинамическим процессом [9]. Равновесные процессы (рис. 1.2) обратимы, т.е. при одном и том же воздействии, в прямом и обратном направлениях, имеют место одни и те же промежуточные состояния. Основным условием обратимости является бесконечно медленное протекание процесса и отсутствие трения. Все реальные процессы неравновесны и необратимы. Поэтому в классической термодинамике рассматривают «квазистатические», как будто бы «равновесные и обратимые процессы. Примеры решения задач
Задача 1. Манометр, измеряющий давление масла в системе смазки двигателя, показывает 0,4 МПа при барометрическом давлении воздуха 765 мм рт. ст. и температуре воздуха 27ºС. Чему равно абсолютное давление масла? Выразить абсолютное давление в барах, мм рт. ст., мм вод. ст., Па, атм. Решение. Абсолютное давление масла определяем по формуле рабс = ризб + В0, где В0 – приведенное к нормальным условиям барометрическое давление В0 = В ± ∆В. ∆В = β · В/1000 – поправка на показания барометра. При положительной температуре поправка берется со знаком «минус». Численные значения коэффициента β приведены в табл. 1.1
Таблица 1.1 Внутренняя энергия системы Согласно молекулярно-кинетической теории газов внутренняя энергия системы является суммой кинетической и потенциальной энергий составляющих ее частиц. Внутренняя энергия системы является функцией термических параметров состояния u = f(P, T, ν). Единицей измерения внутренней энергии в системе СИ является Дж. Внутренняя энергия 1 кграбочего тела называется удельной внутренней энергией (Дж/кг): U = U/m. (2.1) В теплотехнических расчетах используют не абсолютное значение внутренней энергии, а ее изменение: ∆u = Внутренняя энергия системы изменяется только под воздействием внешней среды и является аддитивной величиной, т.е. ее величина равна сумме внутренних энергий частиц, ее составляющих. В термодинамике рассматриваются два типа воздействия внешней среды: – в первом случае в результате действия внешнего давления изменяется внешний параметр системы (объем) и система совершает работу; – во втором случае под воздействием внешней среды (подводом или отводом теплоты) изменяются внутренние параметры и температура. Внутренняя энергия системы при 0ºС принимается равной 0. Работа расширения, сжатия В любом термодинамическом процессе, кроме процесса при V = = const, при подводе к системе теплоты совершается работа против внешних сил. В закрытом цилиндре (рис. 1.2) рабочее тело массой 1 кг при подводе теплоты расширяется от состояния, характеризуемого точкой 1, до состояния, характеризуемого точкой 2. При перемещении поршня на бесконечно малую величину ds рабочее тело в цилиндре совершит работу против внешних сил δl = р × f · ds = pdv,(2.2) так как fds = dv, а f– площадь поршня.
Рис. 2.1. Схема для определения работы расширения Из схемы, представленной на рис. 2.1, следует, что элементарная работа в масштабе равна заштрихованной площадке в системе координат Pv, а конечная работа процесса равна площади
v1 – 1 – 2 – v2 – v1, и зависит от пути, по которому проходит процесс. Работа не является полным дифференциалом, поэтому для ее вычисления необходимо установить зависимость давления от объема. Процесс между состояниями 1 и 2 может проходить как в направлении 1-2, так и в направлении 2-1. Абсолютное давление – величина положительная, приращение объема при расширении: dv > 0, а при сжатии: dv < 0. Можно сделать вывод: 1. При расширении рабочего тела работа термодинамической системы положительна. 2. При сжатии рабочего тела под воздействием внешней среды работа отрицательна. Теплоемкость рабочего тела Отношение количества теплоты, подведенной или отведенной при бесконечно малом изменении системы, к соответствующему изменению температуры называется истинной теплоемкостью С (Дж/К): С = δq/dT. (2.9) Отношение истинной теплоемкости к массе рабочего тела, равной 1 кг, называется удельной массовой теплоемкостью с (Дж/(кг·К)): с = С/m. (2.10) Теплоемкость, отнесенная к молю рабочего тела, называется молярной, обозначается cμ (Дж/(моль·К)): сμ = μ · с. (2.11) Теплоемкость, отнесенная к количеству рабочего тела, содержащемуся в 1 м3 при нормальных физических условиях, называется удельной объемной теплоемкостью. Обозначается с׳ (Дж/(м3·К)): с' = μс/22,4 = с · ρ, (2.12) где r – плотность рабочего тела, кг/м3. Теплоемкость зависит от процесса, так, для адиабатного процесса при δQ = 0 теплоемкость с = 0; в изотермическом процессе dT = 0 и теплоемкость с = ¥. В практических расчетах важнейшее значение имеют теплоемкости при постоянном объеме и постоянном давлении, которые обозначаются как cν и cp соответственно. Между cν и cp установлена связь следующего вида: cp = cν + R, (2.13) μcp = μcν + Rμ. (2.14) Из уравнений (2.2) и (2.5) при ν = const: du = cνdt. (2.15) Формула (2.15) справедлива для любого процесса, так как внутренняя энергия является функцией состояния. Отношение теплоемкостей обозначают символом к: к = ср/сν (2.16) и называют показателем адиабаты. Для одноатомных газов к = 1,66, двухатомных к = 1,4, трехатомных и многоатомных к = 1,29. Экспериментальные исследования показывают, что теплоемкость одноатомных газов практически не зависит от температуры, а теплоемкость двухатомных и трехатомных газов существенно зависит от температуры. Предложены различные математические модели, которые с приемлемой для инженерной практики точностью описывают изменение теплоемкости газов от температуры. Для двухатомных газов модель представляют в виде с = аt + b. (2.17) Для трехатомных газов, например углекислого газа СО2, эта модель имеет вид с = at2 + bt + d, где a, b и d – коэффициенты, численные значения которых приведены в справочной литературе. При больших интервалах изменения температуры в расчетах используют среднее значение температуры в заданном диапазоне. Для определения среднего значения температур в диапазоне от t1 до t2 используют формулу
где cm1 – среднее значение теплоемкости в диапазоне от 0 до t1; cm2 – среднее значение теплоемкости в диапазоне от 0 до t2. Если смесь газов задана массовыми долями, теплоемкость смеси определяется по формуле
Если заданы объемные доли газов
Энтальпия
Энтальпия является важнейшей термодинамической функцией. Ее обозначают hдля одного килограмма рабочего тела и Hдля массыm рабочего тела. Размерность h – Дж/кг и H – Дж. Энтальпию определяют по формуле H = U + pV для массы m ≠ 1 кг (2.21) и по формуле h = u + pν при m = 1 кг. (2.22) Энтальпия зависит от функции состояния – внутренней энергии и термических параметров состояния р и ν. Энтальпия является функцией состояния. При проведении теплотехнических расчетов используют не абсолютное значение энтальпии, а разность энтальпий в конечных точках процесса. Продифференцируем уравнение (2.22), получим dh = du + pdν + νdp. (2.23) Учитывая (2.5), получим
Уравнение (2.24) представляет вторую форму записи первого закона термодинамики. Для изобарического процесса выражение (2.24) примет вид dq = dh. (2.25) После интегрирования (2.25) получим q = h2 – h1. (2.26) Из уравнения (2.25) следует dh = cpdT. (2.27) Уравнение (2.27) справедливо и для любого другого процесса, т.к. энтальпия системы является функцией состояния и ее изменение не зависит от процесса. Энтальпию при 0ºС принимают равной нулю. Энтропия
Теплота не является функцией состояния. Если умножить изменение теплоты на величину 1/T, получим изменение некоторой функции: ds = δq/T, (2.28) которую Клаузиус назвал энтропией. Единицей измерения энтропии, отнесенной к 1 кг газа, является Дж/(кг·К), а для массы газа, не равной одному килограмму, – Дж/К. Запишем формулу (2.28) с учетом формулы (2.5): ds = (du + pdν)/T = cνdT/T + Rdν/ν. (2.29) После интегрирования формулы (2.29) получим s2 – s1 = cνln(T2/T1) + Rln(ν2/ν1). (2.30) Аналогично можно проинтегрировать уравнение (2.28), если воспользоваться для изменения теплоты уравнением (2.24). В результате получим
Из формул (2.30) и (2.31) следует, что изменение энтропии зависит только от начальных и конечных значений параметров. При нормальных условиях энтропия идеального газа принимается равной 0. Примеры решения задач Задача 1. Определить внутреннюю энергию 5 кмоль идеального одноатомного газа при абсолютной температуре, равной 873 К. Решение. Идеальный одноатомный газ имеет три поступательных скорости движения, и формула для определения внутренней энергии имеет вид u = 3RT/2. Газовая постоянная идеального газа равна 8,314 кДж/(кмоль·К). Следовательно, внутренняя энергия будет равна u = 5 · 8,314 · 873 · 3/2 = 54436 Дж. Задача 2. Чему равна работа процесса, если изменение внутренней энергии 3 кг рабочего тела при подводе теплоты в количестве 100 кДж составило 75 кДж? Решение. Для определения работы процесса воспользуемся зависимостью Q = ∆U + L. Из этой формулы следует L = Q – ∆U. После подстановки численных значений входящих в последнюю формулу величин получим L = 100 – 75 кДж. Задача 3. Чему равна энтропия 5 кг воздуха при избыточном давлении р = 19,62 × 104 Па и температуре 1000°С. Принять теплоемкость Ср = const при температуре 1000°С. Решение. По формуле (2.31) изменение энтропии равно s2 – s1 = = cpln(T2/T1) – Rln(p2/p1). Газовая постоянная воздуха R = = 0,287 кДж/(кг·К). По термодинамическим таблицам при температуре 1000°С определяем теплоемкость воздуха ср = 1,185 кДж/(кг·К). Определяем абсолютное давление р = 19,62 · 104 + 9,81 · 104 = 29,43 · 104 Па. Известно, что при температуре 0ºС энтропия принимается равной 0. Таким образом, после подстановки численных значений величин, входящих в формулу (2.30), будем иметь s2 – s1 = 1,185ln(1273/273) – – 0,287ln(29,43 · 104/9,81 · 104) = 1,62 кДж/(кг·К). Для пяти килограммов энтропия будет равна s = 1,62 · 5 = = 8,1 кДж/кг.
Изохорный процесс
1. Характерной особенностью процесса является то, что он осуществляется при постоянном объеме, т.е. ν = const. 2. Уравнение состояния процесса получим из уравнения состояния идеального газа (1.8): p/T = const. 3. Таким образом, между давлением и температурой в изохорном процессе существует прямо пропорциональная зависимость: p2/p1 = = T2/T1. 4. Графическое изображение изохорного процесса в pv и Ts диаграммах представлено на рис. 3.1. 5. Определение теплоты и изменения энтропии процесса: – теплоту, подводимую к системе, определим, используя математическую формулировку первого закона термодинамики (2.5) dq = du + + pdν. В изохорном процессе dν = 0, поэтому dq = du; – в изохорном процессе отношение ν2/ν1 = 1, поэтому уравнение (2.30) принимает вид s2 – s1 = cνln(T2/T1), или в дифференциальной форме ds = cνdT/T. (3.1)
Рис. 3.1. Изображение изохорного процесса в pν- и Ts-диаграммах
6. В изохорном процессе объем не изменяется и работа равна нулю. 7. Теплоемкость изохорного процесса принято обозначать сν. 8. Доля теплоты, расходуемая на увеличение внутренней энергии, определяется по формуле α = du/δq, т.к. в изохорном процессе dq = du, получим α = 1, т.е. вся подведенная к термодинамической системе теплота идет на изменение внутренней энергии. Долю теплоты, которая идет на совершение внешней работы, можно определить по формуле α' = δl/δq = 1 – α. Учитывая, что α = 1, получим α' = 0. Изобарный процесс
1. Характерной особенностью процесса является то, что он осуществляется при постоянном давлении, т.е. p = const. 2. Уравнение состояния процесса получим из уравнения состояния идеального газа (1.8): ν/T = const. 3. Таким образом, между объемом и температурой в изобарном процессе существует прямо пропорциональная зависимость: ν2/ν1 = = T2/T1. 4. Графическое изображение изобарного процесса в pν- и Ts-диаграммах показано на рис. 3.2. 5. Определение теплоты и изменения энтропии процесса: – теплоту определим из уравнения (2.24): Δq = dh – νdp. В изобарном процессе dp = 0, поэтому вся подвденная теплота идет только на изменение энтальпии: δq = dh;
Рис. 3.2. Изображение изобарного процесса в рv- и Ts-диаграммах
– в изобарном процессе p2/p1 = 1, поэтому уравнение (2.31) в дифференциальной форме принимает вид ds = cpdT/T. 6. Работа процесса определяется интегрированием выражения dl = pdν в пределах от ν1 до ν2: l = p(ν2 – ν1). (3.2) 7. Теплоемкость изобарического процесса обозначают cp. 8. Доля теплоты, которая расходуется на увеличение внутренней энергии: α = 1/к, доля теплоты, которая идет на выполнение внешней работы: α' = 1 – 1/к = (к – 1)/к. Изотермический процесс
1. Характерная особенность процесса: T = const. 2. Уравнение состояния процесса: pν = const. 3. Связь между объемом и давлением имеет вид: ν2/ν1 = p1/p2.
Рис. 3.3. Изображение изотермического процесса в рv- и Ts-диаграммах
4. Графическое изображение изотермического процесса в pν- и Ts-диаграммах представлено на рис. 3.3. 5. Определение теплоты и изменения энтропии процесса: – теплота процесса равна работе: δq = δl = pdν; – из уравнений (2.30) и (2.31): учитывая, что T2/T1 = 1, s2 – s1 = = Rln(ν2/ν1) = –Rln(p2/p1) или в дифференциальной форме: ds = Rlnν = –Rlnp. (3.3) 6. Работу изотермического процесса определяют по формуле L = RTln(ν2/ν1) = RTln(p1/p2). (3.4) 7. Теплоемкость изотермического процесса равна ¥. 8. Доля теплоты, которая расходуется на увеличение внутренней энергии: α = du/δq = 0/δq = 0, доля теплоты, которая идет на выполнение внешней работы: α' = 1 – 0 = 1. Таким образом, вся подведенная в изотермическом процессе теплота идет на выполнение работы. Адиабатный процесс 1. Характерной особенностью процесса является то, что он осуществляется при отсутствии теплообмена системы с внешней средой: δq = 0. 2. Уравнение состояния процесса: pvк = const. (3.5) 3. Связь между давлением и объемом: p1ν1к = р2ν2к, или р2/р1 = (ν1/ν2)к. (3.6) Связь между температурой и объемом: Т2/Т1 = (ν1/ν2)к–1. (3.7) Связь между давлением и температурой:
4. Графическое изображение адиабатного процесса в рν- и Ts-диаграммах представлено на рис. 3.4.
Рис. 3.4. Изображение адиабатного процесса в рv- и Ts-диаграммах
5. Определение теплоты и изменения энтропии процесса: – из характеристики адиабатного процесса: δq = 0; – изменение энтропии системы: ds = 0. (3.9) 6. Работа адиабатного процесса определяется по одной из формул: l = (p1ν1 – p2ν2)/(к – 1); l = RT1[1 – p2/p1)(к – 1)/к/(к – 1). (3.10) 7. Теплоемкость адиабатного процесса равна нулю. 8. Доля теплоты, которая расходуется на увеличение внутренней энергии: α = du/0 = ∞, долю теплоты, которая идет на выполнение внешней работы: α' = 1 – ∞ = –∞. Политропный процесс
1. Характерной особенностью процесса является то, что он осуществляется при постоянной теплоемкости с и постоянном показателе политропы n. 2. Уравнение состояния процесса: Pνn = const. (3.11) 3. Связь между давлением и объемом: p1ν1n = р2ν2n, или р2/р1 = (ν1/ν2)n. (3.12) Связь между температурой и объемом: Т2/Т1 = (ν1/ν2)(n – 1)/n. (3.13) Связь между давлением и температурой: Т2/Т1 = (p2/p1)n – 1. (3.14) В формулах (3.11)–(3.14) n = (c – cp)/(c – cν) – показатель политропы. Из уравнения политропного процесса, задавая показателю политропы значения, получим: n = 0, p = const – изобарный процесс; n = 1, pν = const – изотермический процесс; n = к, pνк = const – адиабатный процесс; n = ∞, ν = const – изохорный процесс. 4. Графическое изображение политропного процесса в pν- и
Рис. 3.5. Изображение политропных процессов в рv- и Ts-диаграммах 5. Определение теплоты и изменения энтропии процесса: – теплота в политропном процессе: ∆q = cν(n – к)dT/(n – 1); – изменение энтропии системы: ds = cdT/T. (3.15) 6. Работа политропного процесса (но вместо показателя адиабаты к необходимо подставлять показатель политропы n): l = (p1ν1 – p2ν2)/(n – 1); l = RT1[1 – p2/p1)(n – 1)/n/(n – 1). (3.16) 7. Теплоемкость политропного процесса: с = сν(n – к)/(n – 1). (3.17) Анализ уравнения (3.17) показывает, что в диапазоне 1 < n < ктеплоемкость отрицательна, при этом δQ и dT имеют разные знаки. Работа совершается при подводе теплоты по всем политропам диапазона, кроме адиабаты, т.е. изменение теплоты положительно. Температура рабочего тела в процессе расширения понижается и, таким образом, изменение температуры является отрицательной величиной. 8. Доля теплоты, которая расходуется на увеличение внутренней энергии: α = (n – 1)/(n – к), а доля теплоты, которая идет на выполнение внешней работы: α' = (1 – к)/(n – к). Примеры решения задач Задача 1. В изобарном процессе к термодинамической системе, рабочим телом в которой является СО2, подводится теплота в количестве q = 50 кДж/кг. Определить количество теплоты, расходуемое на выполнение работы и на изменение внутренней энергии. Решение. Доля теплоты, расходуемой на изменение внутренней энергии, в изобарном процессе определяется по формуле α = 1/к. Для трех и более атомных газов показатель адиабаты к = 1,29. Следовательно, доля теплоты на изменение внутренней энергии составит Задача 2. В закрытом сосуде емкостью 0,5 м3 содержится азот при абсолютном давлении 0,5 МПа и температуре 15ºС. Определить абсолютное давление и температуру в сосуде после подвода к азоту 750 кДж тепла. Теплоемкость азота постоянна. Решение. Процесс изохорный. Массу азота в сосуд
|
||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 332; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.12.88 (0.012 с.) |

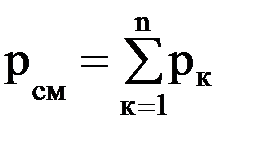 , (1.16)
, (1.16)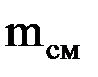 =
= 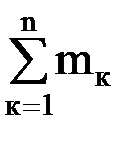 – масса смеси.
– масса смеси.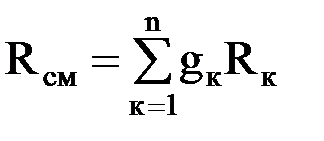 , (1.18)
, (1.18)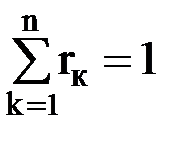 .
.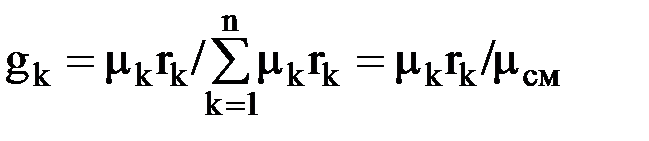 , (1.20)
, (1.20)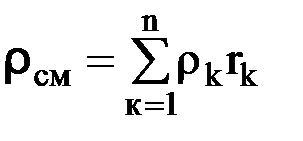 . (1.22)
. (1.22)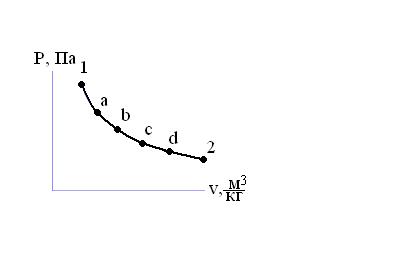
 = u2 – u1, где u1 – численное значение внутренней энергии в начальном состоянии; u2 – численное значение внутренней энергии в конечном состоянии.
= u2 – u1, где u1 – численное значение внутренней энергии в начальном состоянии; u2 – численное значение внутренней энергии в конечном состоянии.
 дляm = 1 кг; (2.3)
дляm = 1 кг; (2.3) для m ¹ 1 кг, (2.4)
для m ¹ 1 кг, (2.4) , (2.18)
, (2.18) . (2.19)
. (2.19) и объемные теплоемкости
и объемные теплоемкости  отдельных газов, то объемная теплоемкость смеси определяется по формуле
отдельных газов, то объемная теплоемкость смеси определяется по формуле . (2.20)
. (2.20) . (2.24)
. (2.24) . (2.31)
. (2.31)


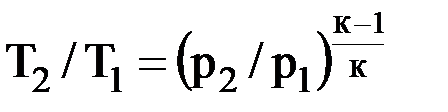 . (3.8)
. (3.8)




