
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальное уравнение теплопроводностиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Дифференциальное уравнение теплопроводности описывает зависимость температуры от времени и текущих координат рассматриваемой точки. Для вывода этой зависимости выделим в температурном поле элемент в виде параллелепипеда со сторонами dx, dy, dz (рис. 8.8). Тепловой поток, входящий в выделенный элемент через поверхность dxdy в направлении оси z, согласно уравнению Фурье, будет равен
Рис. 8.8. К выводу дифференциального уравнения теплопроводности
Аналогично получают величину приращения теплового потока вдоль осей х и у:
Просуммировав уравнения (8.18)–(8.20), получим изменение теплового потока в выделенном элементе:
где dν = dxdyz – объем выделенного элемента; ∆ = ∂2/∂x2 + ∂2/∂y2 + + ∂2/∂z2 – оператор Лапласа. Теплота в элементе идет на изменение внутренней энергии: du = cρ(∂t/∂τ)dν, (8.22) где с – теплоемкость; r – плотность; ∂t/∂τ – производная температуры по времени. Приравняв правые части уравнений (8.21) и (8.22), получим ∂t/∂τ = а (∂2t/∂x2 + ∂2t/∂y2 + ∂2t/∂z2), (8.23) где а – коэффициент температуропроводности, м2/с. При стационарном (установившемся) процессе теплопроводности ∂t/∂τ = 0уравнение (8.23) принимает вид: ∂2t/∂x2 + ∂2t/∂y2 + ∂2t/∂z2 = 0. Решение уравнения (8.23) зависит от начальных и граничных условий, которые определяют однозначность решения задачи. Дифференциальное уравнение конвективного теплообмена
В случае конвективного теплообмена производная по времени зависит также от скорости движения теплоносителя. В общем случае скорость движения изменяется в трех направлениях – х, у, z, поэтому уравнение конвективного теплообмена имеет вид [6]:
В уравнении (8.24): u – проекция скорости на ось х; v – проекция скорости на ось у; w – проекция скорости на ось z. Для упрощения обычно вводят обозначение D/Dτ = ∂t/∂τ + u∂/∂x + + ν∂/∂x + w∂/∂x, с учетом которого уравнение (8.24) можно записать следующим образом: Dt/Dτ = a∆t. (8.25) Оператор Dt/Dτ – субстанциональная производная. Система, состоящая только из одного уравнения и четырех неизвестных (t, u, v, w), незамкнута. Чтобы ее замкнуть, используют уравнения Навье – Стокса и неразрывности. Система, состоящая из уравнения (8.24), уравнений Навье – Стокса и неразрывности является замкнутой, но ее решение для получения коэффициента a представляет весьма сложную задачу, так как входящие в нее уравнения являются нелинейными, многомерными, содержат значительное количество физических параметров. Поэтому для определения коэффициента теплоотдачи a используют эмпирический подход, при этом при планировании и обработке экспериментов используется теория подобия, что позволяет уменьшить количество переменных путем объединения исходных параметров в критерии (числа) подобия. Критерии подобия безразмерные, имеют определенный физический смысл, обозначаются как числа П (Пи) (wτ/l = = П1, RI/U = П2, ma/F = П3 и т.д.) или первыми буквами фамилий ученых, внесших существенный вклад в изучение процессов теплопереноса и гидродинамики. Критерии подобия устанавливаются различными способами: преобразованием уравнений, описывающих данный процесс, к безразмерному виду; путем анализа размерностей; при помощи масштабных преобразований. Если в критерий не входят искомые величины, он называется определяющим. Критерий, в который входят искомые величины, называется неопределяющим. Основные критерии подобия, используемые В теплотехнике
В теплотехнических расчетах наибольшее использование получили следующие критерии подобия: Критерий Нуссельта: Nu = αℓ/λ (8.26) представляет собой отношение между потоком теплоты от жидкости к поверхности тела и потоком теплоты теплопроводностью в теплоносителе у стенки. Критерий содержит коэффициент теплоотдачи a. При известном числе Nuкоэффициент теплоотдачи a определяется по формуле α = Nu λ/ℓ. (8.27) Критерий Рейнольдса: Re = uℓ/ν. (8.28) При течении жидкости в трубах ламинарный режим на стабилизированном участке наблюдается до Критерий Пекле: Pe = uℓ/a (8.29) характеризует отношение между потоком теплоты, переносимой движущимся теплоносителем (конвективным), и потоком теплоты теплопроводностью при одинаковом температурном напоре. Критерий Прандтля равен отношению критерия Пекле к критерию Рейнольдса, т.е. Pr = Pe/Re = ν/a. (8.30) Критерий характеризует соотношение между силами вязкости и конвективным потоком теплоты. Для одноатомных газов численное значение критерия равно 0,67, для двухатомных 1. Для капельных жидкостей значение критерия находится в пределах 1–2500, для жидких металлов предел изменения Прандтля 0,005–0,05. Значение числа Pr приводится в справочниках. Критерий Грасгофа: Критерий Грасгофа определяется по формуле Gr = βpgℓ3∆t/ν2, (8.31) где βp = (1/ν0)(∂ν/∂T)p – коэффициент объемного расширения, К–1; для идеального газа βр = 1/Т; Критерий Грасгофа характеризует гидродинамическое подобие при свободном движении теплоносителя. Он представляет отношение подъемной силы к силе вязкости. Чем выше критерий Грасгофа, тем более интенсивно свободное движение. Критерий Био: Bi = αℓ/λст,(8.32) где ℓ – характерный размер тела, м; λст – коэффициент теплопроводности твердого тела, Вт/(м·К). Критерий характеризует связь между полем температур в твердом теле и условиями теплоотдачи на его поверхности. Коэффициент теплоотдачи a определяют из экспериментально полученных критериальных уравнений следующего вида: Nu = aReβPrγ(Pr/Prc)θ(GrPr)μ. (8.33) Численные значения коэффициентов a, b, g, θ, mможно определять по рекомендациям, изложенным в литературе [1, 2, 3, 4, 5]. Свободное движение теплоносителя Свободное движение теплоносителя осуществляется под действием силы тяжести, вызванной разностью плотностей нагретых и более холодных слоев. Такое движение наблюдается, например, в системах охлаждения пусковых двигателей, при естественной вентиляции воздуха в помещении. В случае свободного движения теплоносителя в большом объеме расчет числа Нуссельта ведут по критериальному уравнению [5]: Nu = C(Gr · Pr)μ · ε. (8.34) В этом уравнении коэффициенты С, e, μ (табл. 8.1) зависят от условий теплоотдачи. Определяющей температурой произведения критериев Gr · Pr является средняя температура теплоносителя в объеме и у стенки: t = 0,5(tc + tж). Таблица 8.1 Численные значения коэффициентов С, e и μ
Теплоотдача при кипении и конденсации Расчет теплоотдачи при кипении используется при расчете производства пара в котельных установках. Интенсивность теплоотдачи зависит от режима кипения. Различают два режима кипения – пузырьковый и пленочный. Пузырьковый режим кипения наблюдается в начале процесса кипения, при этом подводимая теплота от стенки с температурой tст передается примыкающему к ней слою жидкости, в котором температура равна также tст. Температура жидкости изменяется по толщине слоя. Максимальный градиент температур наблюдается в слое жидкости толщиной 3–5 мм, непосредственно примыкающему к поверхности нагрева, а затем изменение температуры незначительно. Разность ∆t = tст – tж называется температурным напором. Центры парообразования зарождаются непосредственно на обогреваемой стенке. При подводе теплоты размеры пузырьков увеличиваются. При определенном соотношении сил поверхностного натяжения и силы тяжести происходит их отрыв от нагреваемой поверхности. К образующимся пузырькам пара теплота подводится от жидкости. Движение пузырьков пара приводит к турбулизации и перемешиванию жидкости и интенсификации теплообмена. При дальнейшем подводе теплоты достигается критический напор ∆t = tст – tж и наступает пленочный режим кипения, при котором пузырьки пара сливаются в сплошную паровую пленку, которая имеет малый коэффициент теплопроводности, и интенсивность теплоотдачи резко падает. Численные значения q, Dt и a, при которых жидкость переходит от пузырькового кипения в пленочный, зависит от рода жидкости, интенсивности перемешивания и других факторов. Для определения коэффициента теплоотдачи можно использовать критериальную зависимость [5]: Nu = CRenPrж0,33. (8.35) Численные значения постоянных С и n в случае кипения неметаллических жидкостей равны: при Re £ 0,01 C = 0,0625, n = 0,5 при Re > 0,01 С = 0,125, n = 0,65. Определяющий размер вычисляется по формуле ℓ = Rкр · (cp∆t/r) · (ρж/ρп), (8.36) где Rкр – критический радиус пузырька; cp∆t – энтальпия перегретой жидкости; r – теплота парообразования; ρж, ρп – плотность жидкой и паровой фаз соответственно. Процесс конденсации пара происходит при охлаждении пара до температуры ниже температуры насыщения при данном давлении. Выделяющееся при этом тепло равно теплоте парообразования. Различают капельную и пленочную конденсацию. Для определения коэффициента теплоотдачи при пленочной конденсации для ламинарного движения можно использовать следующие критериальные уравнения [8]: – для вертикально расположенных труб и стенок: Nu = 0,42K00,28(Prн/Prст)0,25; (8.37) – для горизонтально расположенных труб: Nu = 0,72(K0Prн/Prст)0,25. (8.38) В формулах (8.37) и (8.38) К0 = Ga · Кn · Prн – критерий конденсации; Ga = gℓ3/νн2 – критерий Галилея и критерий Кn = r/(cж · ∆t);
Массообмен В сельскохозяйственном производстве значительное применение получили массообменные процессы: фильтрация влаги в почве, сушка материалов, кондиционирование воздуха. Перенос энергии и вещества осуществляется материальными носителями. Если в изолированной системе содержатся компоненты с неоднородным распределением концентраций, то в ней возникает перенос массы компонентов смеси, стремящейся к установлению равновесного (равномерного) поля концентраций. Перенос массы, также как и перенос теплоты, характеризуется понятиями: «поле», «поток», «сопротивление» и т.д. Перенос вещества в смеси, обусловленный тепловым хаотическим движением микрочастиц вещества (молекул, ионов, атомов), называется молекулярной диффузией. Молекулярная диффузия вследствие неоднородного распределения концентраций в смеси называется концентрационной диффузией. При перемещении, т.е. конвекции, масса компонента переносится макроскопическими элементами смеси. Перенос массы за счет совместного действия молекулярной диффузии и конвективного переноса вещества называется конвективным массообменом. Конвективный массообмен между жидкой (твердой) поверхностью и окружающей средой называется массоотдачей. Плотность потока массы при концентрационной диффузии определяют уравнением, аналогичным уравнению Ньютона – Рихмана: Ji = ρ · βM · (ciп – ci0), (8.39) где bМ – коэффициент массоотдачи, отнесенный к разности концентраций диффундирующего вещества, м/с; сiп и сio – концентрации вещества на поверхности массоотдачи и в окружающей среде. Поток массы от поверхности площадью F определяют по формуле Ji = F · ρ · βM · (ciп – ci0). (8.40)
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 1148; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.174 (0.011 с.) |

 dxdy. Тепловой поток на выходе элемента: dQz+∆z = = –λ(∂t/∂z)dzdxdy – λ(∂2t/∂z2)dzdxdy. Разность тепловых потоков в направлении оси z:
dxdy. Тепловой поток на выходе элемента: dQz+∆z = = –λ(∂t/∂z)dzdxdy – λ(∂2t/∂z2)dzdxdy. Разность тепловых потоков в направлении оси z: . (8.18)
. (8.18)
 ; (8.19)
; (8.19)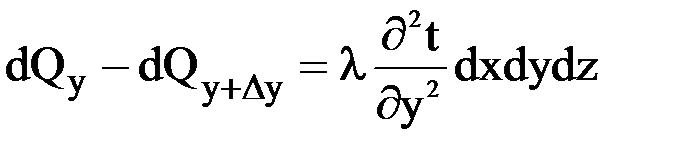 . (8.20)
. (8.20) (8.21)
(8.21) =
=  . (8.24)
. (8.24) , а при Re > 104 устанавливается развитый турбулентный режим (здесь l – внутренний диаметр трубы).
, а при Re > 104 устанавливается развитый турбулентный режим (здесь l – внутренний диаметр трубы). – разность температур в двух точках (потока и стенки), К.
– разность температур в двух точках (потока и стенки), К. r = 103–109
r = 103–109
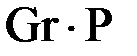 r => 109
r => 109
 )2]
)2]
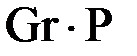 r £ 103
103 £
r £ 103
103 £  r £ 108
r £ 108



