
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теплопроводность диэлектриковСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Теплопроводность твердых тел имеет разную природу в зависимости от типа твердого тела. В диэлектриках, не имеющих свободных электрических зарядов, перенос энергии теплового движения осуществляется фононами. Теплопроводность диэлектриков называют иногда решеточной теплопроводностью, подразумевая, что она обусловлена фононами. Рассмотрим механизм теплопроводности диэлектриков. Считая, что кристалл содержит фононный газ, можно рассматривать явление теплопроводности как явление переноса энергии отдельными фононами. Если бы атомы совершали строго гармонические колебаний, распространяющиеся в решетке в виде системы не взаимодействующих между собой упругих волн, то эти волны распространялись бы в кристалле не рассеиваясь, то есть, не встречая никакого сопротивления, подобно распространению света в вакууме. Если в таком кристалле создать разность температур, то атомы из области, где температура больше, колеблющиеся с большими амплитудами, передавали бы свою энергию соседним атомам, и фронт волны распространялся бы в кристалле со скоростью звука. В отсутствии сопротивления даже при бесконечно малой разности температур тепловой поток мог бы достигать сколь угодно большой величины. Теплопроводность такого кристалла была бы бесконечно большой. В реальных кристаллах колебания атомов носят негармонический характер, что приводит к тому, что нормальные колебания решетки утрачивают независимый характер и взаимодействуют друг с другом, обмениваясь энергией и меняя направление распространения (рассеиваясь). Описание процесса рассеяния нормальных колебаний удобно вести на языке фононов. В случае если нормальные колебания решетки являются независимыми, фононы образуют идеальный газ – газ невзаимодействующих фононов. Переход к негармоническим колебаниям эквивалентен введению взаимодействия между фононами. В кинетической теории газов выводится, что коэффициент теплопроводности газов равен
где l – средняя длина свободного пробега молекул газа, Применим эту формулу к фононному газу, подставив в нее сV – теплоемкость фононного газа,
Температурная зависимость коэффициента теплопроводности решетки определяется зависимостью от температуры длины свободного пробега и теплоемкости. Если экспериментально получить значения К, сV и Экспериментальные данные свидетельствуют о том, что теплопроводность кристаллов на два-три порядка превышает теплопроводность газов (табл.1). Кроме того, теплопроводность металлических кристаллов превышает теплопроводность диэлектрических (табл.1). Например, коэффициент теплопроводности алюминия равен 238 Вт/(м . К), у кварца он не превышает 5 Вт/(мК), а для большинства газов при атмосферном давлении и комнатной температуре примерно равен 30. 10-3 Вт/(м. К). Теплопроводность металлов В металлах в отличие от диэлектриков перенос теплоты осуществляется не только фононами, но и свободными электронами. Поэтому теплопроводность металлов К в общем случае складывается из теплопроводности решетки КРЕШ (обусловленной фононами) и теплопроводности Ке, обусловленной свободными электронами К = КРЕШ + Ке. (9) Теплопроводность электронного газа можно определить на основании (7), подставив в эту формулу
Оценим относительную долю, приходящуюся на решеточную теплопроводность металла. Учитывая соотношения (8) и (10) получим:
Для чистых металлов се/сV» 0,01,
Следовательно, теплопроводность чистых металлов почти полностью определяется теплопроводностью их электронного газа, на долю решеточной проводимости приходится лишь несколько процентов. Этим объясняется высокая теплопроводность металлов по сравнению с неметаллами, в которых фононы – единственные переносчики тепла. Наличие в металлах электронного газа позволяет ожидать, что между электропроводностью твердых тел и их электронной теплопроводностью должна существовать связь. В 1853 году немецкими физиками Г. Видеманом и Р. Францем было экспериментально установлено, что отношение коэффициента теплопроводности К к удельной электропроводности s для металлов при одинаковой температуре постоянно:
В 1881 году датский физик Л. Лоренц экспериментально показал, что это отношение пропорционально температуре Т
где L – число Лоренца, одинаковое практически для всех металлов при комнатной и более высоких температурах. На базе квантовой статистики для числа Лоренца было получено соотношение
где
Выражение (15) получило название закона Видемана-Франца. Практическая часть Идея метода В данной работе для определения коэффициента теплопроводности К используется уравнение Фурье (3). Величины dQ/dt, dT/dх измеряются опытным путем. Внешний вид установки для проведения измерений коэффициента теплопроводности представлен на рис. 3. Исследуемый материал представляет собой сплошной медный или алюминиевый стержень круглого сечения. Стержень покрыт изолирующей пленкой, поэтому можно пренебречь отдачей тепла через боковую поверхность и считать, что тепло распространяется только вдоль стержня. Если существует различие температур между различными частями тела, происходит передача тепла. В этом эксперименте создается одномерный температурный градиент по длине металлического стержня. Для достижения этого верхний конец стержня контактирует с калориметром, в котором кипит вода. Для улучшения контакта стержня и верхнего калориметра используется специальная смазка. Нижний конец стержня опущен в в калориметр с холодной водой (рис. 3). Количество теплоты d Qстержня, переносимое за времяdt, в направлении перпендикулярном поперечному сечению стержня S при наличии температурного градиента dT/dl по длине стержня можно в соответствии с уравнением Фурье (3) найти как
где К – коэффициенттеплопроводности исследуемого вещества, S – площадь поперечного сечения стержня. Вода, находящаяся в нижнем калориметре, служит приемником тепла, переносимого через исследуемый стержень от его горячего конца к холодному. Термометр, погруженный в нижний калориметр, позволяет определить увеличение температуры воды. По длине стержня сделаны небольшие углубления. В эти углубления устанавливают температурные датчики, подключаемые к устройству для измерения температуры. Для улучшения контакта этих датчиков со стержнем необходимо использовать специальную смазку. С помощью датчиков, установленных по длине стержня, можно фиксировать непосредственно разность температур между этими точками для определения градиента температуры. Датчики размещают между наиболее удаленными углублениями на поверхности стержня.
Через некоторое время после начала кипения воды в верхнем калориметре в стержне устанавливается стационарный процесс переноса тепла, характеризуемый постоянством температуры в каждом сечении стержня. Такое состояние возможно, если через любое поперечное сечение за равные промежутки времени проходит одинаковое количество тепла (dQстержня/dt = const), и градиент температуры dT/dl можно считать одинаковым для всех сечений стержня. Он может быть определен в виде:
где l – расстояние между двумя сечениями стержня, ΔТ – разность температур в этих сечениях. Для определения стационарного процесса переноса тепла необходимо фиксировать разность температур между верхней и нижней частью стержня с помощью установленных датчиков. Результаты измерений нужно представить графически в виде зависимости DТ от времени t. Примерный вид зависимости DТ(t) показан на рис. 4. Измерения коэффициента теплопроводности можно начинать, когда DТ практически перестанет изменяться. Из рис. 4 видно, что для представленного графика это происходит спустя примерно 300 секунд после начала измерений.
Рис. 4. Примерный вид зависимости DТ(t). Однако необходимо также учитывать, что вода нагревается (
Подставляя формулы (17) и (18) в уравнение Фурье (16), получим
Выразив К из (19), получим рабочую формулу для определения коэффициента теплопроводности:
Количество теплоты, получаемое водой, находящейся в нижнем калориметре из окружающей среды можно определить, проведя предварительные измерения по определению температуры холодной воды, помещенной в калориметр в течение некоторого промежутка времени. Количество теплоты QОКР, полученное этой водой, в любой момент времени можно рассчитать для как
где Dq = q – qо, q и qо – температуры воды, соответственно в начальный момент времени и момент времени t, С – теплоемкость калориметра. Результаты вычислений необходимо представить в виде графика зависимости QОКР от времени. Примерный вид зависимости QОКР(t) показан на рис. 5. Тангенс угла наклона этого графика будет равен dQОКР/dt. Для определения dQВОДЫ/dt поступают следующим образом. За время t теплота Q будет передана воде, находящейся в нижнем калориметре. При этом вода нагреется от То до Т. Значения температуры воды в нижнем калориметре фиксируются с помощью измерителя температуры PHYWE 4-2. Зная массу воды mВ, находящуюся в нижнем калориметре, можно записать, что
или
где сВ – удельная теплоемкость воды, С – теплоемкость калориметра, То и Т – показания термодатчика, погруженного в нижний калориметр, в начальный момент времени и момент времени t, соответственно. По результатам измерений строится график зависимости количества теплоты, полученного водой Qводы от времени t. dQводы/dt определяется по тангенсу угла наклона графика Qводы(t) аналогично графику, представленному на рис. 5.
Рис. 5. Примерный вид зависимости Qокр(t). Примечание: Упражнения и задания, отмеченные *, выполняются студентами физических специальностей. Упражнение 1*. Нахождение теплоемкости нижнего калориметра 1. Взвесьте нижний калориметр. 2. Определите комнатную температуру qкомн и запишите это значение в лабораторный журнал. Температура нижнего калориметра будет такой же. 3. Отмерьте мерным стаканом примерно 300—350 мл воды из-под крана. 4. Определите температуру воды q1 (примечание: температура воды должна быть немного ниже комнатной). Измерение температуры производится с помощью датчика температуры, подключенного к входу Т3 прибора для измерения температуры PHYWE 4-2. Датчик необходимо опустить в калориметр и зафиксировать при помощи зажимов таким образом, чтобы он не касался дна и стенок калориметра. 5. Заполните нижний калориметр этой водой. 6. Определите температуру воды q2 после помещения ее в калориметр с помощью датчика погружного типа. 7. Рассчитайте теплоемкость калориметра С, используя уравнение теплового баланса:
8. Вылейте воду из калориметра и насухо вытрите его. Упражнение 2*. Расчет тепловых потерь, связанных с теплообменом с окружающей средой. 1. Заполните нижний калориметр определенным количеством холодной воды. Запишите объем воды, помещенной в калориметр. Рассчитайте массу воды.
|
|||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 3175; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.247.237 (0.01 с.) |

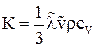 , (7)
, (7) – средняя скорость их теплового движения, сV – удельная теплоемкость газа при постоянном объеме, r – плотность газа.
– средняя скорость их теплового движения, сV – удельная теплоемкость газа при постоянном объеме, r – плотность газа. =
=  – средняя длину свободного пробега фононов, вместо
– средняя длину свободного пробега фононов, вместо  – средняя скорость фононов, r – плотность тела. Скорость фононов
– средняя скорость фононов, r – плотность тела. Скорость фононов  . (8)
. (8) – среднюю длину свободного пробега электронов,
– среднюю длину свободного пробега электронов,  – средняя скорость электронов, се – теплоемкость электронного газа.
– средняя скорость электронов, се – теплоемкость электронного газа. . (10)
. (10)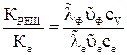 . (11)
. (11)
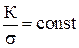 . (12)
. (12) , (13)
, (13) , (14)
, (14) – постоянная Больцмана;
– постоянная Больцмана;  - заряд электрона. Учитывая, что у большинства металлов КРЕШ << Ке, в выражении (12) можно заменить К на Ке, а также используя (13) и (14), соотношение (12) можно записать как
- заряд электрона. Учитывая, что у большинства металлов КРЕШ << Ке, в выражении (12) можно заменить К на Ке, а также используя (13) и (14), соотношение (12) можно записать как . (15)
. (15) , (16)
, (16)



















 (17)
(17)
 ), получая теплоту не только от стержня (
), получая теплоту не только от стержня (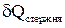 ), но и из окружающей среды (
), но и из окружающей среды ( ). Поэтому нагрев воды только за счет теплоты, полученной от стержня можно учесть, записав следующее соотношение
). Поэтому нагрев воды только за счет теплоты, полученной от стержня можно учесть, записав следующее соотношение . (18)
. (18) . (19)
. (19) . (20)
. (20)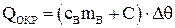 , (21)
, (21) (22)
(22) (23)
(23)
 , (24)
, (24)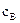 – удельная теплоемкость воды (сВ = 4190 Дж/(кг. К);
– удельная теплоемкость воды (сВ = 4190 Дж/(кг. К); – масса воды; qкомн - комнатную температура; q1 – исходная температура воды; q2 - температура воды после помещения в калориметр.
– масса воды; qкомн - комнатную температура; q1 – исходная температура воды; q2 - температура воды после помещения в калориметр.


