
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение коэффициента теплопроводности металлаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Лабораторная работа №62 Определение коэффициента теплопроводности металла Составители: А.И. Назаров, к.ф.-м.н., д.п.н., профессор О. В. Сергеева, к.ф.-м.н., доцент Рецензент: И.А. Малиненко, к.ф.-м.н., доцент Цель работы: 1. Изучить основы теории теплопроводности металлов. 2. Определить коэффициент теплопроводности для меди и алюминия. 3. Проверить выполнение закона Видемана-Франца. Оборудование: 1. Калориметры, объемом 500 мл 2. Медный и алюминиевый стержни 3. Теплопроводящая паста, 50 г 4. Марлевый мешочек 5. Электроплитка 6. Цифровой термометр, тип 4-2 7. Температурный датчик погружного типа 8. Температурные датчики контактного типа 9. Секундомер 10. Штативы с держателями 11. Стеклянный стакан 12. Магнитная мешалка 13. Кипятильник 14. Весы электронные 15. Мерный цилиндр Теоретическое введение Понятие о теплопроводности в твердых телах. Теплопрово́дность — это перенос теплоты структурными частицами вещества (молекулами, атомами, электронами) в процессе их теплового движения. Такой теплообмен может происходить в любых телах с неоднородным распределением температур, но механизм переноса теплоты будет зависеть от агрегатного состояния вещества. При тепловом контакте двух тел, имеющих различные температуры T1 и T2, происходит передача теплоты от тела с более высокой температурой к телу с более низкой температурой. Такая же передача теплоты происходит между различными частями одного и того же тела, если температуры этих частей неодинаковы. Различают три механизма передачи теплоты: теплопроводность, конвекция и излучение. Излучение рассматривают в оптике. В жидкостях и газах передача теплоты возможна путем теплопроводности и конвекции. В твердом теле конвекция не может возникнуть, так как невозможно перемещение массы вещества вместе с теплом. Поэтому перенос тепла в твердом теле осуществляется только теплопроводностью.
Рис. 1. Процесс теплопроводности, одномерный случай. Механизм переноса тепла в твердом теле описывается так же, как и в газе. Если через единицу площади сечения S перпендикулярно к его плоскости в единицу времени переносится количество тепла dQ, то величина q называется плотностью теплового потока и определяется как
Плотность теплового потока связана с разностью температур, вызывающей перенос вдоль направления х (рис.1) (одномерный случай), соотношением
где К – коэффициент теплопроводности, dT/dx – градиент температуры в направлении х. Смысл градиента температуры заключается в том, что он равен изменению температуры от одной точки к другой, отнесенному к расстоянию между ними. Градиентом скалярной величины является вектор, направленной в сторону ее быстрейшего возрастания. Существование градиента температуры является необходимым условием для возникновения теплопроводности. Знак минус в уравнении (2) означает, что поток тепла направлен в сторону противоположную по направлению градиенту температуры. Если возрастанию х (dx>0) соответствует понижение температуры (dТ < 0), то поток тепла направлен в направлении возрастания х, чтобы уменьшить существующий градиент температуры, который его вызвал. В тех случаях, когда вещество, в котором существует градиент температуры, предоставлено самому себе, к нему извне не подводится энергия, теплопроводность приводит к выравниванию температуры. Такой процесс теплопроводности называют нестационарным. Стационарная теплопроводность наблюдается, если поддерживается постоянный градиент температуры. Объединив соотношения (1) и (2), получим уравнение, которое описывает процесс теплопроводности и называется уравнением Фурье:
Коэффициент К зависит от физической природы вещества и его состояния. Коэффициент теплопроводности численно равен количеству тепла, переносимому за 1 секунду через единицу площади, перпендикулярной направлению распространения тепла, если градиент температуры равен единице. Как следует из формулы (3), коэффициент теплопроводности измеряется в системе СИ в единицах Дж/(м·с·К) или Вт/(м·К). Значения коэффициента теплопроводности для некоторых материалов приведены в табл.1. Как видно из таблицы, металлы обладают большими коэффициентами теплопроводности, они являются хорошими проводниками теплоты. Твердые вещества, являющиеся диэлектриками, как, например, асбест, дерево, лед, и газы, являются плохими проводниками теплоты, поэтому некоторые из них применяются в качестве тепловых изоляторов. На плохой теплопроводности газов, например, основано применение в строительстве пористых материалов. Таблица 1
Величина коэффициента теплопроводности К не может быть вычислена так, как это делается для идеального газа – системы более простой, состоящей из невзаимодействующих частиц. Приближенно коэффициент теплопроводности можно вычислить с помощью квантовых представлений. Фононы и их свойства Атомы твердых тел совершают тепловые колебания около положения равновесия. Вследствие их сильного взаимодействия между собой характер этих колебаний оказывается весьма сложным и точное его описание представляет огромные трудности. Поэтому прибегают к приближенным методам и упрощениям. Вместо того, чтобы рассматривать отдельные колебания частиц. Рассматривают их коллективное движение в кристалле, как в пространственно упорядоченной системе. Такое упрощение основано на том, что вследствие действия сил взаимодействия колебание, возникшее у одной частицы, немедленно передается соседним частицам и в кристалле возбуждается коллективное движение в форме упругой волны, охватывающей все частицы кристалла. Такое коллективное движение называют нормальным колебанием решетки. Каждое нормальное колебание несет с собой энергию и импульс. Энергия нормального колебания решетки равна энергии осциллятора, имеющего массу, равную массе колеблющихся атомов, и колеблющегося с частотой, равной частоте нормального колебания. Нормальные осцилляторы не имеют ничего общего с реальными атомами, кроме одинаковой массы. Каждый осциллятор представляет собой одно из нормальных колебаний решетки. В колебательном движении участвуют все атомы кристалла, совершая его с одной и той же частотой w. Энергия квантового осциллятора определяется следующим соотношением
где w – частота колебаний осциллятора, n – квантовое число,
Рис.2. Энергетический спектр линейного гармонического осциллятора. Квантовая теория позволяет сопоставить распространяющимся в твердом теле сл скоростью звука колебаниям некоторые фиктивные частицы – фононы. Минимальная порция энергии, которую может поглотить или испустить решетка при тепловых колебаниях, соответствует переходу возбуждаемого нормального колебания с данного энергетического уровня на близлежащий соседний и определяется как e = где n – частота фонона. Эту порцию или квант энергии тепловых колебаний решетки называют энергией фонона. Поле упругих волн, заполняющих кристалл, можно трактовать как газ, образованный квантами нормальных колебаний решетки – фононами, обладающими энергией, определяемой по (5) и импульсом р: р = где u – скорость фонона (скорость волны), l – длина упругой звуковой волны. Вектор импульса фонона совпадает с направлением распространения волны. Энергию колебаний атомов кристалла можно представить как сумму энергий отдельных фононов, а кристалл можно считать резервуаром, наполненным своеобразным газом невзаимодействующих частиц – фононов. Основное отличие фононов от настоящих частиц в том, что они могут существовать только внутри кристалла. Фононы не могут существовать в вакууме, как, например, электроны, фотоны. Но там, где они существуют, они ведут себя как настоящие частицы, подчиняясь законам сохранения, проявляя свойства специфических квантовых частиц, перенося в пространстве импульс и энергию. Теплопроводность металлов В металлах в отличие от диэлектриков перенос теплоты осуществляется не только фононами, но и свободными электронами. Поэтому теплопроводность металлов К в общем случае складывается из теплопроводности решетки КРЕШ (обусловленной фононами) и теплопроводности Ке, обусловленной свободными электронами К = КРЕШ + Ке. (9) Теплопроводность электронного газа можно определить на основании (7), подставив в эту формулу
Оценим относительную долю, приходящуюся на решеточную теплопроводность металла. Учитывая соотношения (8) и (10) получим:
Для чистых металлов се/сV» 0,01,
Следовательно, теплопроводность чистых металлов почти полностью определяется теплопроводностью их электронного газа, на долю решеточной проводимости приходится лишь несколько процентов. Этим объясняется высокая теплопроводность металлов по сравнению с неметаллами, в которых фононы – единственные переносчики тепла. Наличие в металлах электронного газа позволяет ожидать, что между электропроводностью твердых тел и их электронной теплопроводностью должна существовать связь. В 1853 году немецкими физиками Г. Видеманом и Р. Францем было экспериментально установлено, что отношение коэффициента теплопроводности К к удельной электропроводности s для металлов при одинаковой температуре постоянно:
В 1881 году датский физик Л. Лоренц экспериментально показал, что это отношение пропорционально температуре Т
где L – число Лоренца, одинаковое практически для всех металлов при комнатной и более высоких температурах. На базе квантовой статистики для числа Лоренца было получено соотношение
где
Выражение (15) получило название закона Видемана-Франца. Практическая часть Идея метода В данной работе для определения коэффициента теплопроводности К используется уравнение Фурье (3). Величины dQ/dt, dT/dх измеряются опытным путем. Внешний вид установки для проведения измерений коэффициента теплопроводности представлен на рис. 3. Исследуемый материал представляет собой сплошной медный или алюминиевый стержень круглого сечения. Стержень покрыт изолирующей пленкой, поэтому можно пренебречь отдачей тепла через боковую поверхность и считать, что тепло распространяется только вдоль стержня. Если существует различие температур между различными частями тела, происходит передача тепла. В этом эксперименте создается одномерный температурный градиент по длине металлического стержня. Для достижения этого верхний конец стержня контактирует с калориметром, в котором кипит вода. Для улучшения контакта стержня и верхнего калориметра используется специальная смазка. Нижний конец стержня опущен в в калориметр с холодной водой (рис. 3). Количество теплоты d Qстержня, переносимое за времяdt, в направлении перпендикулярном поперечному сечению стержня S при наличии температурного градиента dT/dl по длине стержня можно в соответствии с уравнением Фурье (3) найти как
где К – коэффициенттеплопроводности исследуемого вещества, S – площадь поперечного сечения стержня. Вода, находящаяся в нижнем калориметре, служит приемником тепла, переносимого через исследуемый стержень от его горячего конца к холодному. Термометр, погруженный в нижний калориметр, позволяет определить увеличение температуры воды. По длине стержня сделаны небольшие углубления. В эти углубления устанавливают температурные датчики, подключаемые к устройству для измерения температуры. Для улучшения контакта этих датчиков со стержнем необходимо использовать специальную смазку. С помощью датчиков, установленных по длине стержня, можно фиксировать непосредственно разность температур между этими точками для определения градиента температуры. Датчики размещают между наиболее удаленными углублениями на поверхности стержня.
Через некоторое время после начала кипения воды в верхнем калориметре в стержне устанавливается стационарный процесс переноса тепла, характеризуемый постоянством температуры в каждом сечении стержня. Такое состояние возможно, если через любое поперечное сечение за равные промежутки времени проходит одинаковое количество тепла (dQстержня/dt = const), и градиент температуры dT/dl можно считать одинаковым для всех сечений стержня. Он может быть определен в виде:
где l – расстояние между двумя сечениями стержня, ΔТ – разность температур в этих сечениях. Для определения стационарного процесса переноса тепла необходимо фиксировать разность температур между верхней и нижней частью стержня с помощью установленных датчиков. Результаты измерений нужно представить графически в виде зависимости DТ от времени t. Примерный вид зависимости DТ(t) показан на рис. 4. Измерения коэффициента теплопроводности можно начинать, когда DТ практически перестанет изменяться. Из рис. 4 видно, что для представленного графика это происходит спустя примерно 300 секунд после начала измерений.
Рис. 4. Примерный вид зависимости DТ(t). Однако необходимо также учитывать, что вода нагревается (
Подставляя формулы (17) и (18) в уравнение Фурье (16), получим
Выразив К из (19), получим рабочую формулу для определения коэффициента теплопроводности:
Количество теплоты, получаемое водой, находящейся в нижнем калориметре из окружающей среды можно определить, проведя предварительные измерения по определению температуры холодной воды, помещенной в калориметр в течение некоторого промежутка времени. Количество теплоты QОКР, полученное этой водой, в любой момент времени можно рассчитать для как
где Dq = q – qо, q и qо – температуры воды, соответственно в начальный момент времени и момент времени t, С – теплоемкость калориметра. Результаты вычислений необходимо представить в виде графика зависимости QОКР от времени. Примерный вид зависимости QОКР(t) показан на рис. 5. Тангенс угла наклона этого графика будет равен dQОКР/dt. Для определения dQВОДЫ/dt поступают следующим образом. За время t теплота Q будет передана воде, находящейся в нижнем калориметре. При этом вода нагреется от То до Т. Значения температуры воды в нижнем калориметре фиксируются с помощью измерителя температуры PHYWE 4-2. Зная массу воды mВ, находящуюся в нижнем калориметре, можно записать, что
или
где сВ – удельная теплоемкость воды, С – теплоемкость калориметра, То и Т – показания термодатчика, погруженного в нижний калориметр, в начальный момент времени и момент времени t, соответственно. По результатам измерений строится график зависимости количества теплоты, полученного водой Qводы от времени t. dQводы/dt определяется по тангенсу угла наклона графика Qводы(t) аналогично графику, представленному на рис. 5.
Рис. 5. Примерный вид зависимости Qокр(t). Примечание: Упражнения и задания, отмеченные *, выполняются студентами физических специальностей. Упражнение 1*. Нахождение теплоемкости нижнего калориметра 1. Взвесьте нижний калориметр. 2. Определите комнатную температуру qкомн и запишите это значение в лабораторный журнал. Температура нижнего калориметра будет такой же. 3. Отмерьте мерным стаканом примерно 300—350 мл воды из-под крана. 4. Определите температуру воды q1 (примечание: температура воды должна быть немного ниже комнатной). Измерение температуры производится с помощью датчика температуры, подключенного к входу Т3 прибора для измерения температуры PHYWE 4-2. Датчик необходимо опустить в калориметр и зафиксировать при помощи зажимов таким образом, чтобы он не касался дна и стенок калориметра. 5. Заполните нижний калориметр этой водой. 6. Определите температуру воды q2 после помещения ее в калориметр с помощью датчика погружного типа. 7. Рассчитайте теплоемкость калориметра С, используя уравнение теплового баланса:
8. Вылейте воду из калориметра и насухо вытрите его. Упражнение 2*. Расчет тепловых потерь, связанных с теплообменом с окружающей средой. 1. Заполните нижний калориметр определенным количеством холодной воды. Запишите объем воды, помещенной в калориметр. Рассчитайте массу воды. Список литературы 1. Кикоин А. К., Кикоин И. К. Молекулярная физика. М.: Лань, 2007. 2. Сивухин Д.В. Общий курс физики / М.: Наука, 1990. Т.2. 3. Иродов И.Е. Физика макросистем / М.: Наука, 2004. 4. Гершензон Е.М., Малов Н.Н., Мансуров А.Н. Молекулярная физика / М.: АСАDEMA, 2000. 5. Детлаф А.А., Яворский Б.М. Курс физики / М.: Высшая школа, 1981. Т. 2, 3. 6. Трофимова Т. И. Курс физики / М.: Высшая школа, 1998. 7. Шебалин О.Б. Молекулярная физика / М.: Высшая школа, 1978. 8. Епифанов Г.И. Физика твердого тела / М.: Высшая школа, 1977. 9. Бабичев А.П., Бабушкина Н.А., Братковский А.М. и др. Физические величины. Справочник / М.: Энергоатомиздат, 1991. 10. Физический энциклопедический словарь / М.: Советская энциклопедия, 1983.
Лабораторная работа №62 Определение коэффициента теплопроводности металла Составители: А.И. Назаров, к.ф.-м.н., д.п.н., профессор О. В. Сергеева, к.ф.-м.н., доцент Рецензент: И.А. Малиненко, к.ф.-м.н., доцент Цель работы: 1. Изучить основы теории теплопроводности металлов. 2. Определить коэффициент теплопроводности для меди и алюминия. 3. Проверить выполнение закона Видемана-Франца. Оборудование: 1. Калориметры, объемом 500 мл 2. Медный и алюминиевый стержни 3. Теплопроводящая паста, 50 г 4. Марлевый мешочек 5. Электроплитка 6. Цифровой термометр, тип 4-2 7. Температурный датчик погружного типа 8. Температурные датчики контактного типа 9. Секундомер 10. Штативы с держателями 11. Стеклянный стакан 12. Магнитная мешалка 13. Кипятильник 14. Весы электронные 15. Мерный цилиндр Теоретическое введение Понятие о теплопроводности в твердых телах. Теплопрово́дность — это перенос теплоты структурными частицами вещества (молекулами, атомами, электронами) в процессе их теплового движения. Такой теплообмен может происходить в любых телах с неоднородным распределением температур, но механизм переноса теплоты будет зависеть от агрегатного состояния вещества. При тепловом контакте двух тел, имеющих различные температуры T1 и T2, происходит передача теплоты от тела с более высокой температурой к телу с более низкой температурой. Такая же передача теплоты происходит между различными частями одного и того же тела, если температуры этих частей неодинаковы. Различают три механизма передачи теплоты: теплопроводность, конвекция и излучение. Излучение рассматривают в оптике. В жидкостях и газах передача теплоты возможна путем теплопроводности и конвекции. В твердом теле конвекция не может возникнуть, так как невозможно перемещение массы вещества вместе с теплом. Поэтому перенос тепла в твердом теле осуществляется только теплопроводностью.
Рис. 1. Процесс теплопроводности, одномерный случай. Механизм переноса тепла в твердом теле описывается так же, как и в газе. Если через единицу площади сечения S перпендикулярно к его плоскости в единицу времени переносится количество тепла dQ, то величина q называется плотностью теплового потока и определяется как
Плотность теплового потока связана с разностью температур, вызывающей перенос вдоль направления х (рис.1) (одномерный случай), соотношением
где К – коэффициент теплопроводности, dT/dx – градиент температуры в направлении х. Смысл градиента температуры заключается в том, что он равен изменению температуры от одной точки к другой, отнесенному к расстоянию между ними. Градиентом скалярной величины является вектор, направленной в сторону ее быстрейшего возрастания. Существование градиента температуры является необходимым условием для возникновения теплопроводности. Знак минус в уравнении (2) означает, что поток тепла направлен в сторону противоположную по направлению градиенту температуры. Если возрастанию х (dx>0) соответствует понижение температуры (dТ < 0), то поток тепла направлен в направлении возрастания х, чтобы уменьшить существующий градиент температуры, который его вызвал. В тех случаях, когда вещество, в котором существует градиент температуры, предоставлено самому себе, к нему извне не подводится энергия, теплопроводность приводит к выравниванию температуры. Такой процесс теплопроводности называют нестационарным. Стационарная теплопроводность наблюдается, если поддерживается постоянный градиент температуры. Объединив соотношения (1) и (2), получим уравнение, которое описывает процесс теплопроводности и называется уравнением Фурье:
Коэффициент К зависит от физической природы вещества и его состояния. Коэффициент теплопроводности численно равен количеству тепла, переносимому за 1 секунду через единицу площади, перпендикулярной направлению распространения тепла, если градиент температуры равен единице. Как следует из формулы (3), коэффициент теплопроводности измеряется в системе СИ в единицах Дж/(м·с·К) или Вт/(м·К). Значения коэффициента теплопроводности для некоторых материалов приведены в табл.1. Как видно из таблицы, металлы обладают большими коэффициентами теплопроводности, они являются хорошими проводниками теплоты. Твердые вещества, являющиеся диэлектриками, как, например, асбест, дерево, лед, и газы, являются плохими проводниками теплоты, поэтому некоторые из них применяются в качестве тепловых изоляторов. На плохой теплопроводности газов, например, основано применение в строительстве пористых материалов. Таблица 1
Величина коэффициента теплопроводности К не может быть вычислена так, как это делается для идеального газа – системы более простой, состоящей из невзаимодействующих частиц. Приближенно коэффициент теплопроводности можно вычислить с помощью квантовых представлений. Фононы и их свойства Атомы твердых тел совершают тепловые колебания около положения равновесия. Вследствие их сильного взаимодействия между собой характер этих колебаний оказывается весьма сложным и точное его описание представляет огромные трудности. Поэтому прибегают к приближенным методам и упрощениям. Вместо того, чтобы рассматривать отдельные колебания частиц. Рассматривают их коллективное движение в кристалле, как в пространственно упорядоченной системе. Такое упрощение основано на том, что вследствие действия сил взаимодействия колебание, возникшее у одной частицы, немедленно передается соседним частицам и в кристалле возбуждается коллективное движение в форме упругой волны, охватывающей все частицы кристалла. Такое коллективное движение называют нормальным колебанием решетки. Каждое нормальное колебание несет с собой энергию и импульс. Энергия нормального колебания решетки равна энергии осциллятора, имеющего массу, равную массе колеблющихся атомов, и колеблющегося с частотой, равной частоте нормального колебания. Нормальные осцилляторы не имеют ничего общего с реальными атомами, кроме одинаковой массы. Каждый осциллятор представляет собой одно из нормальных колебаний решетки. В колебательном движении участвуют все атомы кристалла, совершая его с одной и той же частотой w. Энергия квантового осциллятора определяется следующим соотношением
где w – частота колебаний осциллятора, n – квантовое число,
Рис.2. Энергетический спектр линейного гармонического осциллятора. Квантовая теория позволяет сопоставить распространяющимся в твердом теле сл скоростью звука колебаниям некоторые фиктивные частицы – фононы. Минимальная порция энергии, которую может поглотить или испустить решетка при тепловых колебаниях, соответствует переходу возбуждаемого нормального колебания с данного энергетического уровня на близлежащий соседний и определяется как e = где n – частота фонона. Эту порцию или квант энергии тепловых колебаний решетки называют энергией фонона. Поле упругих волн, заполняющих кристалл, можно трактовать как газ, образованный квантами нормальных колебаний решетки – фононами, обладающими энергией, определяемой по (5) и импульсом р: р = где u – скорость фонона (скорость волны), l – длина упругой звуковой волны. Вектор импульса фонона совпадает с направлением распространения волны. Энергию колебаний атомов кристалла можно представить как сумму энергий отдельных фононов, а кристалл можно считать резервуаром, наполненным своеобразным газом невзаимодействующих частиц – фононов. Основное отличие фононов от настоящих частиц в том, что они могут существовать только внутри кристалла. Фононы не могут существовать в вакууме, как, например, электроны, фотоны. Но там, где они существуют, они ведут себя как настоящие частицы, подчиняясь законам сохранения, проявляя свойства специфических квантовых частиц, перенося в пространстве импульс и энергию.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 1473; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.247.17 (0.016 с.) |


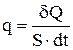 . (1)
. (1) , (2)
, (2) . (3)
. (3) (n = 0, 1, 2, 3…), (4)
(n = 0, 1, 2, 3…), (4) – нормированная постоянная Планка, равная
– нормированная постоянная Планка, равная 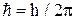 , h – постоянная Планка. На рис. 2 представлен энергетический спектр линейного гармонического осциллятора. Он состоит из дискретных энергетических уровней, отстоящих друг от друга на расстоянии, равном
, h – постоянная Планка. На рис. 2 представлен энергетический спектр линейного гармонического осциллятора. Он состоит из дискретных энергетических уровней, отстоящих друг от друга на расстоянии, равном  .
.
 – среднюю длину свободного пробега электронов,
– среднюю длину свободного пробега электронов,  – средняя скорость электронов, се – теплоемкость электронного газа.
– средняя скорость электронов, се – теплоемкость электронного газа. . (10)
. (10)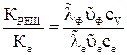 . (11)
. (11) » 5 . 103 м/с,
» 5 . 103 м/с,  » 10-9 м,
» 10-9 м, 
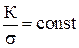 . (12)
. (12) , (13)
, (13) , (14)
, (14) – постоянная Больцмана;
– постоянная Больцмана;  - заряд электрона. Учитывая, что у большинства металлов КРЕШ << Ке, в выражении (12) можно заменить К на Ке, а также используя (13) и (14), соотношение (12) можно записать как
- заряд электрона. Учитывая, что у большинства металлов КРЕШ << Ке, в выражении (12) можно заменить К на Ке, а также используя (13) и (14), соотношение (12) можно записать как . (15)
. (15) , (16)
, (16)



















 (17)
(17)
 ), получая теплоту не только от стержня (
), получая теплоту не только от стержня (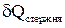 ), но и из окружающей среды (
), но и из окружающей среды ( ). Поэтому нагрев воды только за счет теплоты, полученной от стержня можно учесть, записав следующее соотношение
). Поэтому нагрев воды только за счет теплоты, полученной от стержня можно учесть, записав следующее соотношение . (18)
. (18) . (19)
. (19) . (20)
. (20)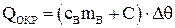 , (21)
, (21) (22)
(22) (23)
(23)
 , (24)
, (24)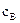 – удельная теплоемкость воды (сВ = 4190 Дж/(кг. К);
– удельная теплоемкость воды (сВ = 4190 Дж/(кг. К); – масса воды; qкомн - комнатную температура; q1 – исходная температура воды; q2 - температура воды после помещения в калориметр.
– масса воды; qкомн - комнатную температура; q1 – исходная температура воды; q2 - температура воды после помещения в калориметр.


