
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теплопроводность при наличии внутренних источников теплотыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте В ряде случаев внутри объектов исследования могут протекать процессы, в результате которых будет выделяться или поглощаться теплота. Выделение теплоты в этом случае характеризуется мощностью источников теплоты qu, Вт/м3. Для стационарного режима теплопроводности дифференциальное уравнение теплопроводности при наличии внутренних источников теплоты имеет вид: Теплопроводность однородной пластины. Рассмотрим длинную пластину, толщина которой 2 d мала по сравнению с двумя другими размерами. Источники теплоты равномерно распределены по объему и равны qu =const. Заданы коэффициенты теплоотдачи a и температура жидкости tж, причем a = const и tж = const. Благодаря равномерному охлаждению температуры обеих поверхностей пластины одинаковы.
При указанных условиях температура пластины будет изменяться только вдоль оси х. Температуру на оси пластины обозначим t0, на ее поверхности – tс. Необходимо определить температуры t0 и tс, распределение температуры в пластине и количество теплоты, отданное в окружающую среду. Дифференциальное уравнение в рассматриваемом случае принимает вид:
Граничные условия: при х = ± d имеем Поскольку граничные условия для обеих сторон пластины одинаковы, температурное поле внутри пластины должно быть симметричным относительно плоскости х = 0. Это означает, что можно далее рассматривать лишь одну половину пластины, например, правую и записать граничные условия для нее в виде: х = 0; х = d; После интегрирования дифференциального уравнения получим:
Постоянные интегрирования С1 и С2 определяются из граничных условий по выражению для первой производной: при х = 0 получаем С1 = 0; при х = d получаем Подставим это значение в исходное значение для граничного условия х = d
Подставив это выражение в уравнение полученное после второго интегрирования при х = d получим:
Подставив значения постоянных С1 и С2 в исходное выражение, найдем уравнение температурного поля:
Из полученного уравнения следует, что температура в плоской стенке в случае симметричной задачи распределяется по параболическому закону. В рассматриваемой задаче тепловой поток изменяется вдоль оси х:
При х = 0 плотность теплового потока q = 0. Тепловой поток с единицы поверхности пластины при х = d
Общее количество теплоты, отданное всей поверхностью в единицу времени (вся поверхность F равна двум боковым поверхностям F 1):
Теплопроводность однородного цилиндрического стержня. Рассмотрим круглый цилиндр, радиус которого мал по сравнению с длиной цилиндра. При этих условиях температура будет изменяться только вдоль радиуса. Внутренние источники теплоты равномерно распределены по объему тела. Заданы температура окружающей среды tж = const и постоянный по всей поверхности коэффициент теплоотдачи.
при r = r 0 Необходимо найти уравнение температурного поля и тепловой поток, а также значения температур на оси t0 и на поверхности tc. Проинтегрируем дифференциальное уравнение теплопроводности. При этом произведем замену
Тогда уравнение теплопроводности запишется в виде:
После интегрирования получим:
После второго интегрирования получим:
Постоянные интегрирования С1 и С2 определяются из граничных условий при r = 0 получаем С1 = 0; при r = r 0 получаем Подставив последнее выражение в граничные условия, получим:
Подставив это выражение в уравнение полученное после второго интегрирования при r = r 0 получим:
Подставив значения постоянных С1 и С2 в исходное выражение, найдем уравнение температурного поля:
Полученное выражение показывает, что распределение температуры в круглом стержне подчиняется параболическому закону. Из полученного уравнения при r = 0 найдем температуру на оси цилиндра:
Плотность теплового на поверхности цилиндра равна:
Полный тепловой поток с поверхности цилиндра равна:
Контрольные вопросы
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 692; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 .
.
 .
. .
. ;
;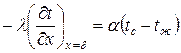 .
. ;
;  .
. .
. Þ
Þ  .
. Þ
Þ  .
. Þ
Þ  .
. .
. .
.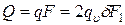 .
.
 .
Граничные условия:
при r = 0
.
Граничные условия:
при r = 0  ;
;
 .
.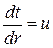 .
.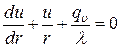 Þ
Þ  .
. Þ
Þ  .
. .
. .
. Þ
Þ  .
. .
. .
. .
. .
.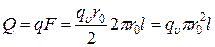 .
.


