Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Численное решение квазилинейных многомерных уравнений теплопроводности с разрывными коэффициентамиСодержание книги
Поиск на нашем сайте
Введение Актуальность В настоящее время одной из актуальных задач нефтегазовой отрасли является всестороннее изучение возможности использования армированных полимерных труб (АПТ) в газораспределительных сетях до 1,2 МПа и выше [1-4]. Для обоснования эффективности и изменения нормативной базы по применению АПТ, отстающей от требований производства, наряду с исследованием механического поведения трубопроводов в различных условиях эксплуатации разрабатываются способысоединения армированных труб. АПТ состоит из трех слоев: внутреннего и внешнего из полиэтилена и промежуточного – армирующего (рис. 1), полученного намоткой арамидными нитями. Сварка как способ соединения является приоритетным при монтаже конструкций из армированных труб. Наличие армирующих нитей определяет требование, чтобы обрезанный торец трубы был защищен от окружающей и транспортируемой среды. Это достигается, например, выполнением двух стандартных операций: сваркой встык с последующим удалением наружного грата и усилением сварного шва при помощи муфтовой сварки [2]. При этом для выполнения стыковой сварки концы армировки срезаются на определенную глубину. Другой способ защиты армирующих нитей заключается в соединении на концы АПТ специальных сварочных гильз с закладными нагревателями и последующей муфтовой сварке труб. В данной работе рассматривается второй способ сварки, поскольку при этом используется сварка с помощью деталей с закладными нагревателями, более удобный с точки зрения проведения автоматической сварки. Согласно нормативным документам сварку полиэтиленовых труб для газопроводов можно проводить при температурах окружающего воздуха (ОВ) от -15 °С до 45 °С [5]. При более низких температурах ОВ сварочные работы рекомендуется выполнять в отапливаемых помещениях (укрытиях), обеспечивающих соблюдение заданного температурного интервала. Однако такая сварка связана с большими энергетическими, непроизводительными затратами и длительной подготовкой, что недопустимо в аварийных ситуациях. Актуальной проблемой является разработка методов и средств оперативной сварки АПТ в регионах с холодным климатом, где температуры ОВ достигают значений ниже минус 15 °С. В работе [6] предложен способ стыковой сварки полиэтиленовых труб при температурах воздуха ниже нормативных. При низких температурах ОВ технологические режимы, обеспечивающие такую же динамику температурного поля, что и при допустимых температурах ОВ, определяются на основе математического моделирования теплового процесса сварки [7–9]. Перспективным является развитие предложенного подхода регулирования динамикой температурного поля с использованием математического моделирования теплового процесса для сварки АПТ с помощью гильз. В данной работе рассматривается этап нагрева, на котором при сварке гильзы в условиях низких температур необходимо обеспечить такую же границу проплавления, что и при допустимых температурах воздуха. Цель работы Целью работы является разработка алгоритма численного решения задачи определения нестационарного температурного поля при приварке сварочной гильзы в полимерных армированных трубах. Для достижения цели поставлены следующие задачи: · Поставить задачу Стефана для определения нестационарного температурного поля при приварке сварочной гильзы в полимерных армированных трубах с учетом теплоты фазового перехода при оплавлении и кристаллизации полиэтилена; · Изучить методы численного решения фронтовой задачи Стефана и выбрать наиболее эффективный метод для решения поставленной задачи; · Построить алгоритм численного решения задачи.
Глава I Численное решение квазилинейных многомерных уравнений теплопроводности с разрывными коэффициентами
Разностная схема — это конечная система алгебраических уравнений, поставленная в соответствие какой-либо дифференциальной задаче, содержащей дифференциальное уравнение и дополнительные условия (например: краевые условия и/или начальное распределение). Таким образом, разностные схемы применяются для сведения дифференциальной задачи, имеющей континуальный характер, к конечной системе уравнений, численное решение которых принципиально возможно на вычислительных машинах. Алгебраические уравнения, поставленные, в соответствие дифференциальному уравнению получаются применением разностного метода, что отличает теорию разностных схем от других численных методов решения дифференциальных задач. Аппроксимация. Научный метод, состоящий в замене одних объектов другими, в том или ином смысле близкими к исходным, но более простыми. Аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов. Устойчивость. Условия аппроксимации не достаточно для того, чтобы результат разностной схемы приближался к точному ответу при h→0. В случае схем, коэффициенты которых не зависят от решения дифференциального уравнения, нужно выполнение условия устойчивости. Такие схемы можно представить как некоторый линейный оператор, который преобразует значения функции в момент t в значения функции в момент t+τ. Условие устойчивости требует, чтобы собственные числа (вообще говоря комплексные) этого оператора не превосходили по модулю 1+ch, где с — некоторая константа, при h→0. Если это условие не выполнено, то погрешности схемы быстро возрастают и результат тем хуже, чем меньше шаг. Если выполнены как условие аппроксимации, так и условие устойчивости, то результат разностной схемы сходится к решению дифференциального уравнения.
Методы сквозного счета
Двухфазная задача Стефана Классическая задача Стефана допускает обобщенную формулировку в виде одного нелинейного уравнения теплопроводности, при которой реализуются необходимые условия на границе фазового перехода. Это дает возможность строить вычислительные алгоритмы приближенного решения задач с фазовыми превращениями без явного выделения свободной границы. О таких методах мы говорим как о методах сквозного счета. Рассматривается модельная двухфазная задача Стефана в прямоугольнике Запишем в каждой подобласти уравнение теплопроводности
В начальный момент задается некоторое распределение температуры:
Температуру фазового перехода принимаем равной нулю и поэтому свободная граница
На ней выполнены два условия сопряжения, отражающие непрерывность температуры и закон сохранения тепла:
где λ — энтальпия фазового перехода, a Рассматриваемая двухфазная задача Стефана (1)-(6) может быть записана в виде одного общего уравнения теплопроводности во всей области
Здесь коэффициенты теплоемкости и теплопроводности разрывны и имеют вид
В соответствии с (2) и (3) уравнение (7) дополняется условиями
Особенность задачи Стефана проявляется в наличии слагаемого с δ функцией в левой части уравнения (7). Выделение или поглощение тепла при фазовом переходе соответствует наличию сосредоточенной теплоемкости на границе фазового перехода. Сама краевая задача (7)-(9) не очень сильно отличается от рассмотренных выше квазилинейных задач теплопроводности. Это позволяет нам перейти к построению соответствующих разностных схем.
Разностная схема со сглаженными коэффициентами
Простейший подход к приближенному решению задачи Стефана в формулировке (7)-(9) состоит в том, что коэффициенты уравнения (7) сглаживаются, т. е. совершается переход к обычной задаче теплопроводности. В уравнении (7) теплоемкость
При необходимости проводится сглаживание и коэффициента теплопроводности (
В вычислительной практике получили распространение различные аппроксимационные формулы для
В качестве второго примера может отметить параболическую аппроксимацию, когда
для которой условие
также, очевидно, выполнено. Как показывают численные эксперименты, точность разностного решения слабо зависит от выбора той или иной аппроксимационной формулы для δ -функции, в частности, от выбора (12) либо (13). Более существенное влияние оказывает величина параметра сглаживания В методах сквозного счета разностную схему строят на основе использования уравнения (11), считая коэффициенты этого уравнения достаточно гладкими. Сама граница фазового перехода не выделяется, не участвует в построении разностной схемы. При необходимости свободная граница идентифицируется как нулевая изотерма после того, как решение найдено. Для решения задачи (8), (9), (11) применяются рассмотренные ранее разностные методы. Применим, например, чисто неявную разностную схему
здесь
Граничные и начальные условия (8), (9) дают
Для определенности положим
Реализация нелинейной разностной схемы (14)—(19) осуществляется на основе итерационных методов. Простейший из них связан с итерационным уточнением коэффициентов. Новое приближение находится из решения линейной разностной задачи
Как правило, достаточно нескольких итераций (20), (21), чтобы обеспечить хорошую точность. Вместо итерационного процесса (20), (21) можно использовать метод Ньютона, который приводит к несамосопряженной сеточной эллиптической задаче для нового приближения.
Глава II
Постановка задачи
Расчетная схема трубы с гильзой представлена на рис. 1. Рис. 1. Расчетная схема трубы с гильзой: 1 – стенка трубы; 2 – армирующий слой; 3 – воздух внутри трубы; 4 – сварочная гильза
Не теряя общности, будем считать, что гильза и основной материал трубы изготовлены из одного и того же материала. Предполагается, что распределение температуры в трубе и гильзе однородно по окружности, воздух внутри трубы неподвижен. Математическая задача ставится следующим образом. Область W, занятая гильзой и отрезком трубы, в момент времени t >0 разбивается некоторой гладкой поверхностью Г(t), подлежащей определению, на две подобласти
где T(r,z,t) – температура в момент времени t; с(Т) – коэффициент теплоемкости; r(Т) – удельная плотность; l(Т) – коэффициент теплопроводности; tm – время расчета; r, z – цилиндрические координаты; r1 – внутренний радиус трубы и гильзы; r2 – внешний радиус гильзы со спиралью; r3 – внешний радиус трубы. Индекс i= 1 для твердой фазы материала трубы; i= 2 для жидкой фазы материала трубы; i =3 для воздуха. Нагревательный элемент рассматривается как сосредоточенный источник тепла:
где Q(t) – мощность источника; z1, z2 – координаты начала и конца спирали соответственно. Распределение температуры в трубе и гильзе в начальный момент времени однородно, температура стенки равна температуре окружающего воздуха Т0:
На границе трубы и гильзы задается условие идеального теплового контакта:
На левой границе гильзы при z = 0 задается конвективный теплообмен с окружающим воздухом:
Учитывая низкую теплопроводность полиэтилена, примем, что на некотором удалении от зоны сварки температура трубы не изменяется на протяжении всего времени протекания процесса. Таким образом, на другом торце трубы задается условие:
На внутренней поверхности трубы и гильзы задается условие:
На внешней поверхности трубы происходит конвективный теплообмен с окружающим воздухом:
При r = 0 задается условие ограниченности решения:
Для учета теплоты фазового перехода при плавлении (кристаллизации) воспользуемся традиционной постановкой задачи Стефана. На границе раздела фаз кроме равенства температуры материала температуре фазового перехода
задается условие Стефана
где
Рис. 2 Конструкция трубы
Рис. 3. Подготовленная внутренняя поверхность трубы и монтаж сварочной гильзы: 1 – трубы; 2 – сварочная гильза
Алгоритм задачи Стефана
Для решения задачи Стефана используем метод сглаживания коэффициентов с применением разностных схем сквозного счета [14], тем самым совершаем переход к обычной задаче теплопроводности.
Здесь коэффициенты теплоемкости и теплопроводности имеют вид:
или
Далее задачу теплопроводности приведем к цепочке одномерных задач. Расщепление по r и z. Заключение.
· Предложена математическая модель теплового процесса приварки сварочной гильзы в полиэтиленовую армированную трубу для газопроводов; · Разработан алгоритм численного решения двумерной задачи Стефана для определения нестационарного температурного поля при приварке сварочной гильзы в полимерных армированных трубах;
Список использованной литературы
1. Пепеляев В.С., Тараканов А.И. Полиэтиленовые трубы, армированные синтетическими нитями для нефтепромысловых трубопроводов // Интервал. Передовые нефтегазовые технологии. – 2006. - №9. –С. 33-37. 2. Пепеляев В.С., Тараканов А.И. Полиэтиленовые армированные трубы для газопроводов с рабочим давлением свыше 1,2 Мпа // Полимергаз. – 2006. -№4. –С. 14-18. 3. Пепеляев В.С., Тараканов А.И. Выбор методики испытаний промысловых трубопроводов из полиэтиленовых армированных синтетическими нитями труб // Оборудование и технологии для нефтегазового комплекса. – 2007. -№3. –С. 78-80. 4. Галичанин Е.Н. Применение новых технологий в транспортировке углеводородного сырья // Нефть. Газ. Промышленность. – 2007. -№1(29). –С. 52-55. 5. СП 42-103-2003. Проектирование и строительство газопроводов из полиэтиленовых труб и реконструкция изношенных газопроводов. – М.:Полимергаз, ФГУП ЦПП, 2004. -86 с. 6. Пат. РФ. №2343331 RUF16L 13/00, 47/00. Способ сварки полимерных труб / Старостин Н.П., Герасимов А.И., Аммосова О.А.; Институт проблем нефти и газа СО РАН. – 2006144681/06; заявл. 14.12.2006; опубл. 10.01.2009, Бюл. №1. 7. Старостин Н.П., Аммосова О.А. Математическое моделирование теплового процесса при сварке полиэтиленовых труб встык при температурах воздуха ниже нормативных // Вестник машиностроения. – 2009. 8. Старостин Н.П., Аммосова О.А. Контактная сварка полимерных труб оплавлением при низких температурах окружающей среды. Математическое моделирование теплового процесса // Сварочное производство. -2007. -№1. –С. 17-20. 9. Старостин Н.П., Аммосова О.А. Контактная сварка полиэтиленовых труб оплавлением при низких температурах окружающей среды Ч.2. Исследование процесса охлаждения // Сварочное производство. – 2008. – № 9. – С. 31–34. 10. Самарский А.А., Моисеенко Б.Д. Экономичная схема сквозного счета для многомерной задачи Стефана // Журн. вычислит. матем. и мат. физики. – 1965. – Т. 5., №5. – С.816–827. 11. Старостин Н.П., Егорова М.П., Герасимов А.И. Температурный режим при электромуфтовой сварке полиэтиленовых труб для газопроводов // Нефтегазовое дело, 2009.http://www.ogbus.ru/authors/Starostin/Starostin_3.pdf 12. Родионов А.К., Бабенко Ф.И., Коваленко Н.А. Трещиностойкость сварных стыковых соединений полиэтиленовых труб // Материалы. Технологии. Инструменты. – 2003.. – Т. 8. – № 3. – С. 19–20. 13. Самарский А.А. Теория разностных схем. М. Наука, 1983. –С. 69-97. 14. Самарский А.А. Вабищевич П.Н. Вычислительная теплопередача. Москва – 2003. –С. 341-362. 15. Охлопков Н.М. Численные методы и вычислительные алгоритмы. Часть 1. Якутск, ЯГУ, 1994. 16. Охлопков Н.М. Численные методы и вычислительные алгоритмы. Часть 2. Якутск, ЯГУ, 1995. 17. Охлопков Н.М. Численные методы и вычислительные алгоритмы. Часть 3. Якутск, ЯГУ, 1996. 18. Охлопков Н.М. Численные методы решения краевых задач математической физики. Якутск, ЯГУ, 1993. 19. Васильев В.И., Максимов А.М. Тепломассоперенос в промерзающих и протаивающих грунтах. Москва 1997. –С. 116-136. 20. Бондарев Э.А., Васильев В.И. Задача Стефана с неизвестной температурой фазового перехода. 1984. Минск –T.7. –С. 155-159. 21. Мейрманов A.M. Зaдaчa Cтeфaнa. - Hoвoсибиpск: Нayкa, 1986. –С. 240. 22. Авдонин Н.А. Математическое описание процессов кристаллизации. –Рига: Зинатне, 1980. –С. 169. 23. Самарский А.А., Гулuн А.B. Численные методы. М: Наука, 1989. –С.432. 24. Бакирова О.И. О некоторых методах решения задачи Стефана. 1983. №3. –С. 491-500.
Введение Актуальность В настоящее время одной из актуальных задач нефтегазовой отрасли является всестороннее изучение возможности использования армированных полимерных труб (АПТ) в газораспределительных сетях до 1,2 МПа и выше [1-4]. Для обоснования эффективности и изменения нормативной базы по применению АПТ, отстающей от требований производства, наряду с исследованием механического поведения трубопроводов в различных условиях эксплуатации разрабатываются способысоединения армированных труб. АПТ состоит из трех слоев: внутреннего и внешнего из полиэтилена и промежуточного – армирующего (рис. 1), полученного намоткой арамидными нитями. Сварка как способ соединения является приоритетным при монтаже конструкций из армированных труб. Наличие армирующих нитей определяет требование, чтобы обрезанный торец трубы был защищен от окружающей и транспортируемой среды. Это достигается, например, выполнением двух стандартных операций: сваркой встык с последующим удалением наружного грата и усилением сварного шва при помощи муфтовой сварки [2]. При этом для выполнения стыковой сварки концы армировки срезаются на определенную глубину. Другой способ защиты армирующих нитей заключается в соединении на концы АПТ специальных сварочных гильз с закладными нагревателями и последующей муфтовой сварке труб. В данной работе рассматривается второй способ сварки, поскольку при этом используется сварка с помощью деталей с закладными нагревателями, более удобный с точки зрения проведения автоматической сварки. Согласно нормативным документам сварку полиэтиленовых труб для газопроводов можно проводить при температурах окружающего воздуха (ОВ) от -15 °С до 45 °С [5]. При более низких температурах ОВ сварочные работы рекомендуется выполнять в отапливаемых помещениях (укрытиях), обеспечивающих соблюдение заданного температурного интервала. Однако такая сварка связана с большими энергетическими, непроизводительными затратами и длительной подготовкой, что недопустимо в аварийных ситуациях. Актуальной проблемой является разработка методов и средств оперативной сварки АПТ в регионах с холодным климатом, где температуры ОВ достигают значений ниже минус 15 °С. В работе [6] предложен способ стыковой сварки полиэтиленовых труб при температурах воздуха ниже нормативных. При низких температурах ОВ технологические режимы, обеспечивающие такую же динамику температурного поля, что и при допустимых температурах ОВ, определяются на основе математического моделирования теплового процесса сварки [7–9]. Перспективным является развитие предложенного подхода регулирования динамикой температурного поля с использованием математического моделирования теплового процесса для сварки АПТ с помощью гильз. В данной работе рассматривается этап нагрева, на котором при сварке гильзы в условиях низких температур необходимо обеспечить такую же границу проплавления, что и при допустимых температурах воздуха. Цель работы Целью работы является разработка алгоритма численного решения задачи определения нестационарного температурного поля при приварке сварочной гильзы в полимерных армированных трубах. Для достижения цели поставлены следующие задачи: · Поставить задачу Стефана для определения нестационарного температурного поля при приварке сварочной гильзы в полимерных армированных трубах с учетом теплоты фазового перехода при оплавлении и кристаллизации полиэтилена; · Изучить методы численного решения фронтовой задачи Стефана и выбрать наиболее эффективный метод для решения поставленной задачи; · Построить алгоритм численного решения задачи.
Глава I Численное решение квазилинейных многомерных уравнений теплопроводности с разрывными коэффициентами
Разностная схема — это конечная система алгебраических уравнений, поставленная в соответствие какой-либо дифференциальной задаче, содержащей дифференциальное уравнение и дополнительные условия (например: краевые условия и/или начальное распределение). Таким образом, разностные схемы применяются для сведения дифференциальной задачи, имеющей континуальный характер, к конечной системе уравнений, численное решение которых принципиально возможно на вычислительных машинах. Алгебраические уравнения, поставленные, в соответствие дифференциальному уравнению получаются применением разностного метода, что отличает теорию разностных схем от других численных методов решения дифференциальных задач. Аппроксимация. Научный метод, состоящий в замене одних объектов другими, в том или ином смысле близкими к исходным, но более простыми. Аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов. Устойчивость. Условия аппроксимации не достаточно для того, чтобы результат разностной схемы приближался к точному ответу при h→0. В случае схем, коэффициенты которых не зависят от решения дифференциального уравнения, нужно выполнение условия устойчивости. Такие схемы можно представить как некоторый линейный оператор, который преобразует значения функции в момент t в значения функции в момент t+τ. Условие устойчивости требует, чтобы собственные числа (вообще говоря комплексные) этого оператора не превосходили по модулю 1+ch, где с — некоторая константа, при h→0. Если это условие не выполнено, то погрешности схемы быстро возрастают и результат тем хуже, чем меньше шаг. Если выполнены как условие аппроксимации, так и условие устойчивости, то результат разностной схемы сходится к решению дифференциального уравнения.
|
||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 390; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.85.233 (0.015 с.) |

 . Свободная граница
. Свободная граница  разбивает
разбивает 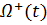 и
и  . В обоих подобластях выполняется уравнение теплопроводности. Как обычно, будем считать, что теплофизические параметры твердой и жидкой фаз постоянны, для обозначения принадлежности к той или иной области будем использовать индекс «+» или «-».
. В обоих подобластях выполняется уравнение теплопроводности. Как обычно, будем считать, что теплофизические параметры твердой и жидкой фаз постоянны, для обозначения принадлежности к той или иной области будем использовать индекс «+» или «-».




 — скорость движения свободной границы по нормали к
— скорость движения свободной границы по нормали к 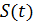 .
. — дельта-функция, тогда вместо уравнений (1) и условий сопряжения (4)-(6) можно рассматривать одно уравнение теплопроводности
— дельта-функция, тогда вместо уравнений (1) и условий сопряжения (4)-(6) можно рассматривать одно уравнение теплопроводности


 и слагаемое
и слагаемое 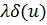 входят одинаковым образом. Заменим δ-функцию
входят одинаковым образом. Заменим δ-функцию  некоторой функцией
некоторой функцией  , которая отлична от нуля только внутри интервала сглаживания
, которая отлична от нуля только внутри интервала сглаживания  , и введем эффективную сглаженную теплоемкость
, и введем эффективную сглаженную теплоемкость
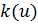 заменяется на
заменяется на 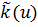 ) и вместо уравнения (7) ищется решение уравнения со сглаженными коэффициентами
) и вместо уравнения (7) ищется решение уравнения со сглаженными коэффициентами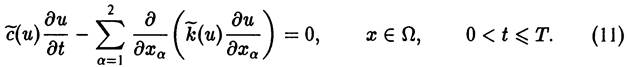

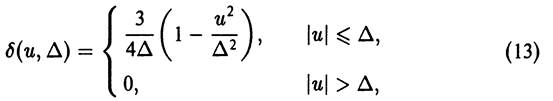

 , который естественно зависит от используемой сетки и определяется, чаще всего, эмпирически в результате методических расчетов.
, который естественно зависит от используемой сетки и определяется, чаще всего, эмпирически в результате методических расчетов.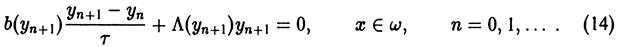



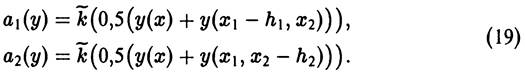


 и
и 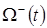 , занятые соответственно жидкой и твердой фазами материала трубы и гильзы. В каждой из областей
, занятые соответственно жидкой и твердой фазами материала трубы и гильзы. В каждой из областей  удовлетворяет двумерному уравнению теплопроводности в цилиндрических координатах:
удовлетворяет двумерному уравнению теплопроводности в цилиндрических координатах: (1)
(1) ,
, (2)
(2) . (3)
. (3) . (4)
. (4) ,
,  (5)
(5) . (6)
. (6) , (7)
, (7)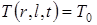 . (8)
. (8)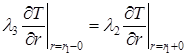 ,
, . (9)
. (9) . (10)
. (10) . (11)
. (11) (12)
(12)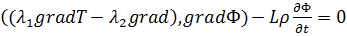 (13)
(13) - уравнение положения границы раздела фаз Г(t) в момент времени t; L,
- уравнение положения границы раздела фаз Г(t) в момент времени t; L, 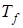 – удельная теплота и температура фазового перехода соответственно.
– удельная теплота и температура фазового перехода соответственно.

 (1)
(1) (2’)
(2’) (3’)
(3’)
 (2’’)
(2’’) (3’’)
(3’’)