Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод суммарной аппроксимацииСодержание книги
Поиск на нашем сайте
Необходимо указать общий метод получения экономичных схем, пригодных для уравнений с переменными и даже разрывными коэффициентами, для квазилинейных нестационарных уравнений в случае произвольной области любого числа измерений.
в произвольной р-мерной области G с границей Г, если заданы
Квазилинейное уравнение теплопроводности соответствует случаю
Конечно, термин «произвольная область» нельзя понимать буквально. Граница Г области должна быть достаточно гладкой, чтобы обеспечить существование гладкого решения u =u(х, t) исходной задачи (1)—(2). При оценке погрешности аппроксимации и точности разностных схем мы всегда предполагаем, что решение исходной задачи для дифференциального уравнения существует и имеет нужные по ходу изложения производные. Все экономичные методы имеют одну общую алгоритмическую идею: процесс отыскания приближенного решения многомерной задачи разбивается на несколько этапов, на каждом из которых решается простая задача. Так, например, для уравнений второго порядка параболического или гиперболического типа такой простой, «первичной», алгебраической задачей является трехточечная разностная задача (разностное уравнение второго порядка), которая решается методом прогонки. Эта трехточечная разностная задача, как правило, может быть трактована как разностная. аппроксимация одномерного (по
Пусть дано многомерное уравнение:
где L—линейный дифференциальный оператор, действующий на u(х,t) как функцию х,
Так, например, если
то Поставим задаче в соответствие цепочку «одномерных» уравнений (первую цепочку).
перепишем в виде
где
полагая при этом
Решением этой задачи назовем значения Каждое из уравнений
заменим разностной схемой:
В простейшем случае это двухслойная схема, связывающая значения
Например, это может быть схема с весами
где
Методы решения задачи Стефана
Задача о фазовом переходе Важный класс нелинейных проблем теплообмена связан с процессами фазовых превращений. Мы рассматриваем переходы твердое тело—жидкость. Для моделирования процессов плавления/кристаллизации чистых веществ используется классическая модель Стефана, которая характеризуется заданием постоянной температуры на границе фазового перехода[24]. Пусть имеются две фазы с коэффициентами теплопроводности и теплоемкости
На границе раздела фаз температура постоянна и равна температуре фазового перехода,
границы фазового перехода ξ удовлетворяет уравнению
если в первой фазе Вводя σ-функцию, уравнение запишем в виде
|
||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 306; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.42.59 (0.005 с.) |

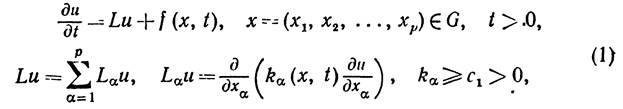
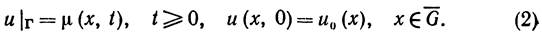
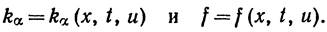
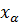 ) дифференциального уравнения. Таким образом, экономичный алгоритм решения сложных задач есть цепочка простых алгоритмов. Отсюда становятся понятными применяемые различными авторами термины для экономичных методов решения многомерных задач — метод переменных направлений (на каждом этапе решается одномерная задача по фиксированному направлению
) дифференциального уравнения. Таким образом, экономичный алгоритм решения сложных задач есть цепочка простых алгоритмов. Отсюда становятся понятными применяемые различными авторами термины для экономичных методов решения многомерных задач — метод переменных направлений (на каждом этапе решается одномерная задача по фиксированному направлению 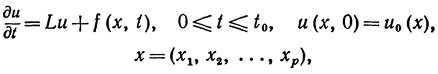
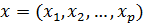 —точка р-мерной области G с границей Г, на которой заданы некоторые граничные условия. Для построения экономичных методов основную роль играет возможность представления оператора L в виде суммы операторов более простой структуры
—точка р-мерной области G с границей Г, на которой заданы некоторые граничные условия. Для построения экономичных методов основную роль играет возможность представления оператора L в виде суммы операторов более простой структуры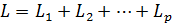
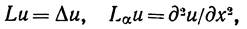
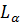 есть оператор второй производной по аргументу
есть оператор второй производной по аргументу 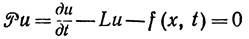
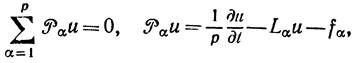
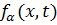 ,
, 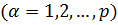 – произвольные функции, удовлетворяющие условию нормировки
– произвольные функции, удовлетворяющие условию нормировки 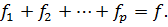 На отрезке
На отрезке 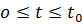 введем равномерную сетку
введем равномерную сетку 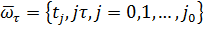 с шагом
с шагом 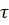 . Каждый интервал разобьем на
. Каждый интервал разобьем на 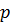 частей, введя точки
частей, введя точки 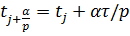 ,
, 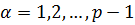 и обозначая
и обозначая 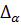 – полуинтервал
– полуинтервал 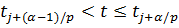 . Будем последовательно решать уравнения
. Будем последовательно решать уравнения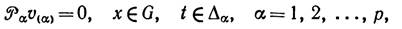
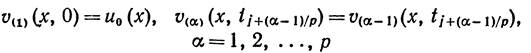
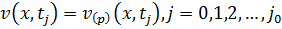 .
.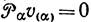 или
или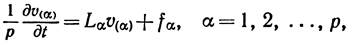
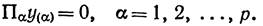
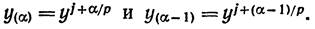
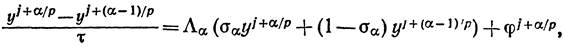
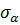 – произвольный параметр,
– произвольный параметр, 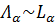 .
.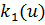 ,
, 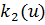 и
и 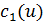 ,
, 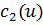 . В каждой фазе температура удовлетворяет уравнению
. В каждой фазе температура удовлетворяет уравнению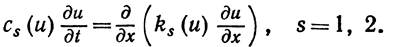
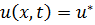 . Скорость движения
. Скорость движения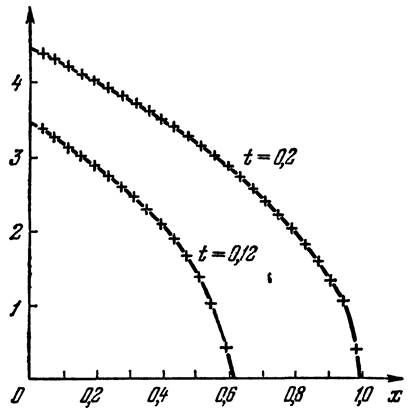
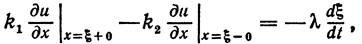
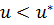 , во второй
, во второй 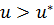 .
.