
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение задачи теплопроводности по радиальной переменнойСодержание книги
Поиск на нашем сайте
Имеем цилиндрически-симметричную задачу теплопроводности:
С начальными условиями:
Краевыми условиями:
В месте расположения спирали задается условие сосредоточенного источника тепла:
Обозначим L:
Введем сетку:
L аппроксимируем:
Задачу аппроксимируем методом баланса. Функции кусочно-непрерывны, поэтому
Возьмем σ=1. Получаем неявную разностную схему,
Разностная схема определена на шаблоне: * * * * Коэффициенты являются нелинейными функциями, таким образом приходим к нелинейному уравнению теплопроводности и для нахождения ее решения используется метод итераций
Относительно Задача в точке
Граничное условие (3) аппроксимируем методом баланса, σ=1:
Аппроксимируем краевое условие (4) приr=0, σ=1:
Получим систему линейных алгебраических уравнений с трехдиагональной матрицей [15-18]. Такая система решается методом прогонки:
Найдем коэффициенты системы:
Решение задачи теплопроводности по осевой переменной
Имеем обычную задачу теплопроводности в декартовых координатах:
С начальными условиями:
Краевыми условиями:
Введем сетку:
Задачу аппроксимируем методом баланса. Функции кусочно-непрерывны, поэтому
Возьмем σ=1. Получаем неявную разностную схему. Коэффициенты являются нелинейными функциями, таким образом приходим к нелинейному уравнению теплопроводности и для нахождения ее решения используется метод итераций:
Граничное условие (3) аппроксимируем методом баланса Возьмем σ=1
Условие (4) первого рода аппроксимируется точно:
Получаем систему линейных алгебраических уравнений с трехдиагональной матрицей. Решаем методом прогонки:
Найдем коэффициенты системы:
В качестве начального приближения берется функция температуры с предыдущего шага по времени: Заключение.
· Предложена математическая модель теплового процесса приварки сварочной гильзы в полиэтиленовую армированную трубу для газопроводов; · Разработан алгоритм численного решения двумерной задачи Стефана для определения нестационарного температурного поля при приварке сварочной гильзы в полимерных армированных трубах;
Список использованной литературы
1. Пепеляев В.С., Тараканов А.И. Полиэтиленовые трубы, армированные синтетическими нитями для нефтепромысловых трубопроводов // Интервал. Передовые нефтегазовые технологии. – 2006. - №9. –С. 33-37. 2. Пепеляев В.С., Тараканов А.И. Полиэтиленовые армированные трубы для газопроводов с рабочим давлением свыше 1,2 Мпа // Полимергаз. – 2006. -№4. –С. 14-18. 3. Пепеляев В.С., Тараканов А.И. Выбор методики испытаний промысловых трубопроводов из полиэтиленовых армированных синтетическими нитями труб // Оборудование и технологии для нефтегазового комплекса. – 2007. -№3. –С. 78-80. 4. Галичанин Е.Н. Применение новых технологий в транспортировке углеводородного сырья // Нефть. Газ. Промышленность. – 2007. -№1(29). –С. 52-55. 5. СП 42-103-2003. Проектирование и строительство газопроводов из полиэтиленовых труб и реконструкция изношенных газопроводов. – М.:Полимергаз, ФГУП ЦПП, 2004. -86 с. 6. Пат. РФ. №2343331 RUF16L 13/00, 47/00. Способ сварки полимерных труб / Старостин Н.П., Герасимов А.И., Аммосова О.А.; Институт проблем нефти и газа СО РАН. – 2006144681/06; заявл. 14.12.2006; опубл. 10.01.2009, Бюл. №1. 7. Старостин Н.П., Аммосова О.А. Математическое моделирование теплового процесса при сварке полиэтиленовых труб встык при температурах воздуха ниже нормативных // Вестник машиностроения. – 2009. 8. Старостин Н.П., Аммосова О.А. Контактная сварка полимерных труб оплавлением при низких температурах окружающей среды. Математическое моделирование теплового процесса // Сварочное производство. -2007. -№1. –С. 17-20. 9. Старостин Н.П., Аммосова О.А. Контактная сварка полиэтиленовых труб оплавлением при низких температурах окружающей среды Ч.2. Исследование процесса охлаждения // Сварочное производство. – 2008. – № 9. – С. 31–34. 10. Самарский А.А., Моисеенко Б.Д. Экономичная схема сквозного счета для многомерной задачи Стефана // Журн. вычислит. матем. и мат. физики. – 1965. – Т. 5., №5. – С.816–827. 11. Старостин Н.П., Егорова М.П., Герасимов А.И. Температурный режим при электромуфтовой сварке полиэтиленовых труб для газопроводов // Нефтегазовое дело, 2009.http://www.ogbus.ru/authors/Starostin/Starostin_3.pdf 12. Родионов А.К., Бабенко Ф.И., Коваленко Н.А. Трещиностойкость сварных стыковых соединений полиэтиленовых труб // Материалы. Технологии. Инструменты. – 2003.. – Т. 8. – № 3. – С. 19–20. 13. Самарский А.А. Теория разностных схем. М. Наука, 1983. –С. 69-97. 14. Самарский А.А. Вабищевич П.Н. Вычислительная теплопередача. Москва – 2003. –С. 341-362. 15. Охлопков Н.М. Численные методы и вычислительные алгоритмы. Часть 1. Якутск, ЯГУ, 1994. 16. Охлопков Н.М. Численные методы и вычислительные алгоритмы. Часть 2. Якутск, ЯГУ, 1995. 17. Охлопков Н.М. Численные методы и вычислительные алгоритмы. Часть 3. Якутск, ЯГУ, 1996. 18. Охлопков Н.М. Численные методы решения краевых задач математической физики. Якутск, ЯГУ, 1993. 19. Васильев В.И., Максимов А.М. Тепломассоперенос в промерзающих и протаивающих грунтах. Москва 1997. –С. 116-136. 20. Бондарев Э.А., Васильев В.И. Задача Стефана с неизвестной температурой фазового перехода. 1984. Минск –T.7. –С. 155-159. 21. Мейрманов A.M. Зaдaчa Cтeфaнa. - Hoвoсибиpск: Нayкa, 1986. –С. 240. 22. Авдонин Н.А. Математическое описание процессов кристаллизации. –Рига: Зинатне, 1980. –С. 169. 23. Самарский А.А., Гулuн А.B. Численные методы. М: Наука, 1989. –С.432. 24. Бакирова О.И. О некоторых методах решения задачи Стефана. 1983. №3. –С. 491-500.
|
||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 187; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.90.161 (0.008 с.) |

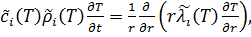 (1)
(1)
 (2)
(2) (3)
(3) (4)
(4) (5)
(5)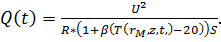 (6)
(6) (7)
(7)
 ,
, .
. (8)
(8)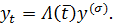 (9)
(9)

 (10)
(10)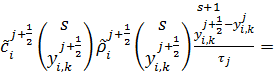
 (11)
(11) разностная схема оказывается линейной.
разностная схема оказывается линейной. имеет в наличии сосредоточенный источник тепла и удовлетворяет условию сопряжения. Уравнение примет вид
имеет в наличии сосредоточенный источник тепла и удовлетворяет условию сопряжения. Уравнение примет вид (12)
(12) (13)
(13) (14)
(14)
 (15)
(15) ,
, .
.
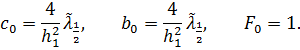

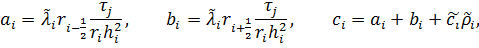



 (1)
(1)
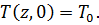 (2)
(2) (3)
(3) (4)
(4)
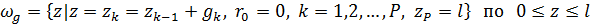 ,
, .
.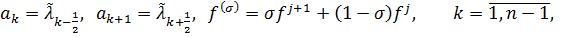

 . (4)
. (4)


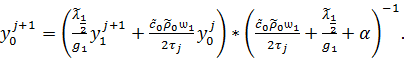 (5)
(5)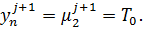






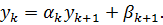
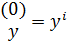 . Прекращаем итерации по условию:
. Прекращаем итерации по условию: 



