
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальное уравнение теплопроводности.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Сделаем допущения: · Тело однородно и изотропно. · Физические параметры постоянны. · Деформация рассматриваемого объема, связанная с изменением температуры, очень мала по сравнению с самим объемом. В основе вывода положен закон сохранения энергии. Количество теплоты
Выделим элементарный объем.
Количество теплоты, отведенное через противоположную грань элементарного параллелепипеда в направлении оси OX запишется
Разница между количеством теплоты, подведенного к элементарному параллелепипеду, и количеством теплоты, отведенного от него за
или
Функция
Взяв два первых члена ряда:
Аналогично для других осей:
Количество теплоты
Для второй составляющей
Третья составляющая в уравнении (*) найдется в зависимости от характера термодинамического процесса изменения системы. Вся теплота подведенная к элементарному объему, уйдет на изменение внутренней энергии вещества, заключенного в этом объеме.
Для внутренней энергии объема.
Подставляя полученное выражение в (*) получим:
или
Учитывая то, что проекции вектора плотности теплового потока на координатные оси OX, OY, OZ:
Подставляя это в (**), получим:
или
Это дифференциальное уравнение теплопроводности. Если теплофизические характеристики постоянны:
Из уравнения видно, что 1.
2.
Так как дифференциальное уравнение теплопроводности выводится на основе общих законов физики, то оно описывает явления теплопроводности в самом общем виде. Для выделения конкретного вопроса и дать его полное математическое описание, к дифференциальному уравнению необходимо присоединить математическое описание всех частных особенностей рассматриваемого процесса. Эти частные особенности, которые совместно с дифференциальным уравнением дают полное математическое описание конкретного процесса теплопроводности называется условиями однозначности или краевыми условиями. Условия однозначности включают в себя: 1. Геометрические условия, характеризующие форму и размеры тела, в котором протекает процесс. 2. Физические условия, характеризующие физические свойства среды и тела 3. Взаимные (начальные) условия, характеризующие распределение температур в изучаемом теле в начальный момент времени 4. Граничные условия, характеризующие взаимодействия рассматриваемого тела с окружающей средой. Граничными условиями задается форма и линейные размеры тела, в котором протекает процесс Физическими условиями задаются физические параметры тела, и может быть задан закон распределения внутренних источников тепла. Начальные условия необходимы при рассмотрении нестационарных процессов и состоят в задании закона распределения температуры внутри тела в начальный момент времени. Граничные условия могут быть заданы несколькими способами Граничные условия первого рода задается распределение температуры на поверхности тела для каждого момента времени
Граничные условия второго рода з адаются значения теплового потока для каждой точки поверхности и любого момента времени
Граничные условия третьего рода задается температура окружающей среды и закон теплообмена между поверхностью тела и окружающей средой. Граничные условия третьего рода характеризуют закон теплообмена между поверхностью и окружающей средой в процессе охлаждения и нагрева.
Иногда ни одно из перечисленных граничных условий задать невозможно. Тогда для определения теплового взаимодействия между телами приходится решать сопряженную задачу. При решении таких задач должны выполняться условия равенства температур и тепловых потоков по обе стороны отграницы раздела. В общем случае условия сопряженности можно записать:
При отсутствии на границе раздела сред процессов с выделением или поглощением теплоты, условия сопряженности принимают вид:
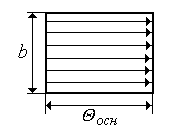
ТЕПЛО.Вопрос№4 Сравнение штыревых и ребристых радиаторов. Оценка производится для одинаковых габаритов либо для одинаковых режимов транзисторов. У штыревых радиаторов выигрыш до 40% в обоих случаях, как при естественной, так и при вынужденной конвекции. 1. высота ребра не должна быть более 40мм. 2. поверхность оребрения (частота рёбер) не должна превышать более чем в 5-6 раз основание радиатора. Идеальное ребро -ребро, у которого температурный напор по всей высоте одинаков.
Практические рекомендации. Оценку эффективности ребра ведут по следующему соотношению:
При повышении числа ребер возрастает теплоотдающая поверхность радиатора, но уменьшается расстояние между ребрами, что приводит к увеличению Конструктивные рекомендации. 1. При охлаждении радиаторов за счёт естественной конвекции воздушные каналы необходимо располагать вертикально. При установке радиаторов на горизонтальное шасси снизу необходимо предусматривать отверстия для подвода воздуха, или поднимать радиатор над шасси на расстояние не менее оптимального межрёберного. 2. При обдуве воздухом каналы необходимо располагать по направлению движения воздуха.
|
||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 560; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.01 с.) |

 введенное в элементарный объем
введенное в элементарный объем  извне за время
извне за время 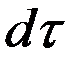 вследствие теплопроводности, а также от внутренних источников, равно изменению внутренней энергии вещества, содержащегося в элементарном объеме.
вследствие теплопроводности, а также от внутренних источников, равно изменению внутренней энергии вещества, содержащегося в элементарном объеме.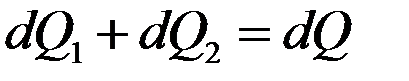 (*)
(*)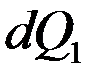 - количество теплоты введенное в элементарный объем путем теплопроводности за время
- количество теплоты введенное в элементарный объем путем теплопроводности за время 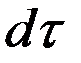
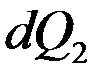 - количество теплоты, которая за время
- количество теплоты, которая за время 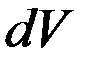 за счет внутренних источников.
за счет внутренних источников. - изменение внутренней энергии вещества в объеме
- изменение внутренней энергии вещества в объеме 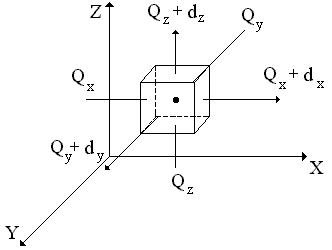
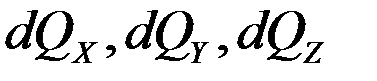 - количество теплоты, подводимое к граням элементарного объема за
- количество теплоты, подводимое к граням элементарного объема за 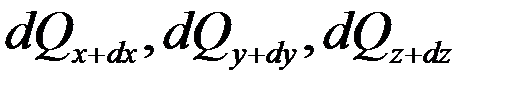 - количество теплоты, подводимое через противоположные грани в тех же направлениях.
- количество теплоты, подводимое через противоположные грани в тех же направлениях.
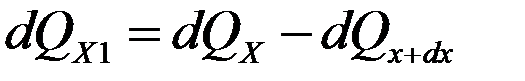
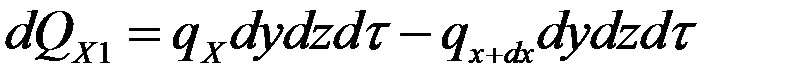
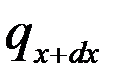 является непрерывной в рассматриваемом интервале и может быть разложена в ряд Тейлора.
является непрерывной в рассматриваемом интервале и может быть разложена в ряд Тейлора.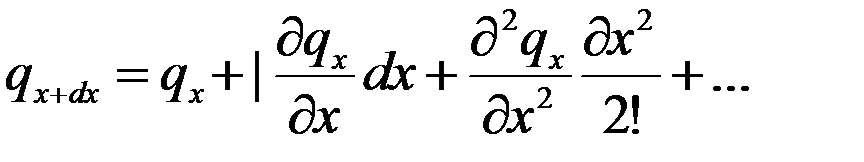
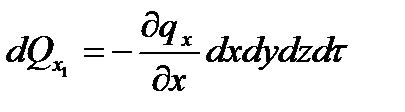
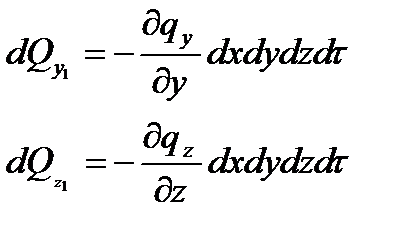
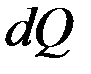 , подведенное в результате теплопроводности к рассматриваемому объекту будет равно:
, подведенное в результате теплопроводности к рассматриваемому объекту будет равно: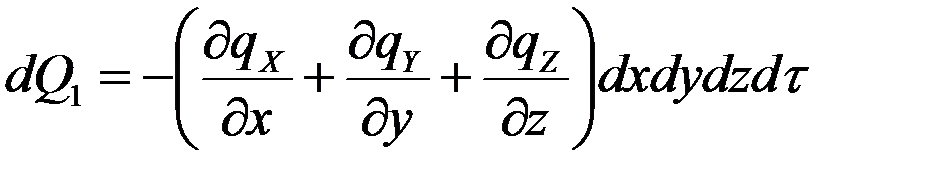
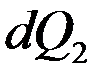 . Количество теплоты, выделенное внутренними источниками в единицу объема среды в единицу времени через
. Количество теплоты, выделенное внутренними источниками в единицу объема среды в единицу времени через 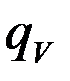 тогда:
тогда: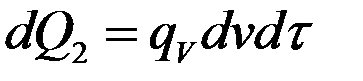
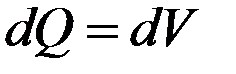
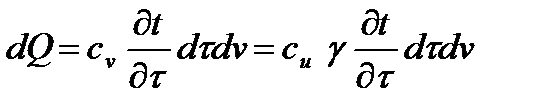
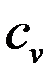 - теплоемкость единицы объема,
- теплоемкость единицы объема, - теплоемкость единицы массы,
- теплоемкость единицы массы,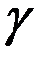 - плотность вещества.
- плотность вещества.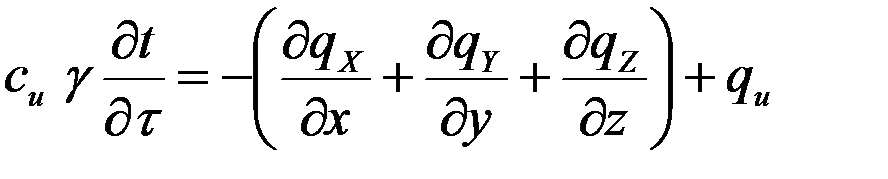 (**)
(**)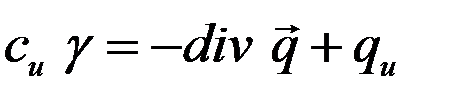

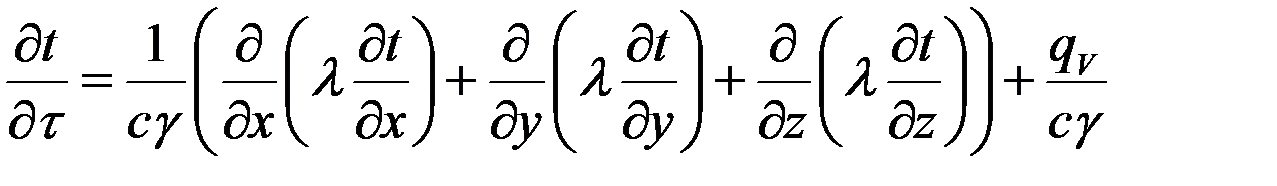
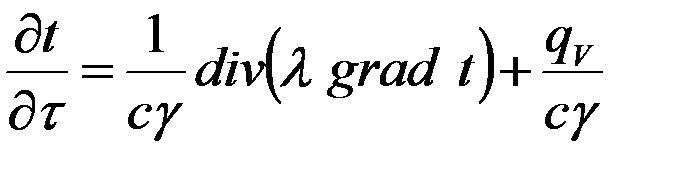

 - изменение температуры со временем.
- изменение температуры со временем.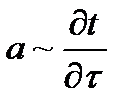 , где a - коэффициент температуропроворности – характеризует скорость изменения температуры.
, где a - коэффициент температуропроворности – характеризует скорость изменения температуры.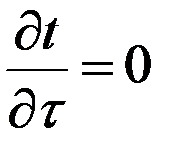 - стационарный тепловой режим
- стационарный тепловой режим - уравнение Пуассона
- уравнение Пуассона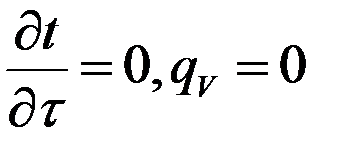 - нет внутренних источников тепла.
- нет внутренних источников тепла.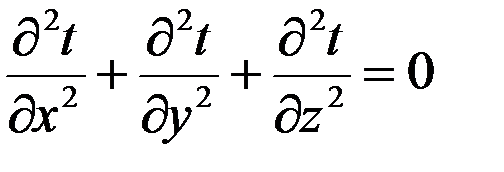 - уравнение Лапласа.
- уравнение Лапласа.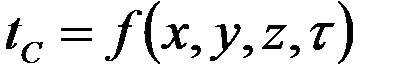
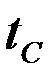 - температура поверхности тела
- температура поверхности тела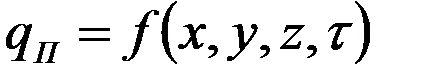
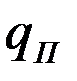 - плотность теплового потока на поверхности тела
- плотность теплового потока на поверхности тела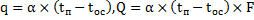

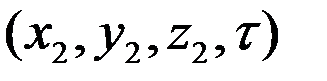 - источники теплоты на поверхности границы
- источники теплоты на поверхности границы - координаты поверхности раздела сред
- координаты поверхности раздела сред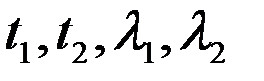 - температуры и коэффициенты теплопроводности сред.
- температуры и коэффициенты теплопроводности сред.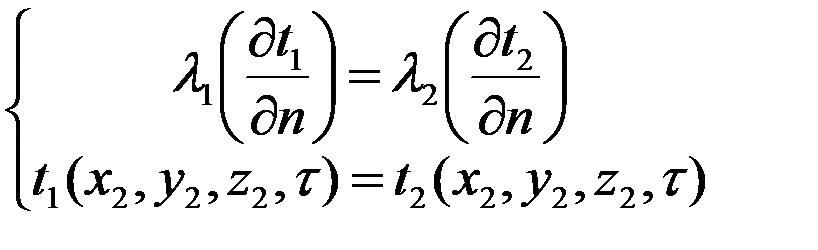
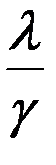 . Чем оно выше, тем эффективнее материал.
. Чем оно выше, тем эффективнее материал.
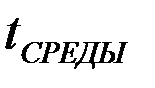 между рёбрами, а следовательно и к уменьшению конвективной составляющей теплообмена. При этом уменьшается также и радиационная составляющая теплообмена за счёт многократного переотражения в пространстве между рёбрами.
между рёбрами, а следовательно и к уменьшению конвективной составляющей теплообмена. При этом уменьшается также и радиационная составляющая теплообмена за счёт многократного переотражения в пространстве между рёбрами.


