
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статический и динамический расчетСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Статический расчет системы
2. Определение координат центра тяжести объекта. Исходным при проектировании системы амортизации являются не только параметры внешних механических воздействий, но и законченная компоновка устройства, т.е. считаются известными габариты устройства (блока), место установки, габариты, масса различных частей блока (узлы, детали), кроме этого существуют ограничения на типоразмер амортизатора. Необходимым является наличие всех характеристик для применяемого типа амортизатора. На первом этапе в блоке аппаратуры выделяются элементарные узлы простейшей геометрической формы. При этом из сборочного чертежа всегда можно определить координаты центра тяжести этого элементарного блока относительно любой выбранной первоначальной системы координат. Для элементарного блока координаты его центра тяжести должны быть достаточно просто определяемыми. Рекомендуется первоначально выбирать систему так, чтобы одна ось проходила через ребро куба.
Масса элементарного блока также должна быть известна. Форма элементарного блока должна быть такова, чтобы определение собственных моментов инерции этого блока было возможно по таблицам (см. п. 2.1). X, Y, Z – координаты центра тяжести блока, относительно выбранной первоначально системы координат.
После определения центра тяжести блока координатные оси переносятся в эту точку и весь последующий расчет ведется относительно этих новых координат.
3. Определение реакций амортизаторов. Различают две схемы нагружения амортизаторов: а) однонаправленная схема; б) пространственная схема нагружения. а) Однонаправленная схема нагружения должна отвечать следующим условиям: - реакция амортизаторов и нагрузка на них образуют систему паралельных сил; - блок в положении равновесия должен устанавливаться без перекосов;
Pi -реакции амортизаторов Эта система возможна при установке блоков без перекосов. В однонаправленной схеме нагружения неизвестной является реакция амортизатора и число неизвестных зависит от количества амортизаторов. Реакции амортизаторов определяются на основе уравнений статистики. Для однонаправленной схемы:
при n = 3, ищем P1, P2, P3, (система из 3-х уравнений). При n = 3 система статически определима, и мы из исходной системы непосредственно находим три неизвестных реакции. При n = 4 система статически неопределима и необходимо четвертое уравнение. Его получают за счет введения дополнительного условия на расположение амортизаторов. Дополнительные условия задаются за счет соответствующего выбора координат установки амортизаторов. Для такой системы P1 = P2 = P3 = P4 = G/4. Здесь дополнительное условие – симметрия амортизаторов – вылилось в подобное решение системы.
Всегда при
2. Здесь дополнительное условие таково:
для того, чтобы система была статически определима необходимо задать n = 3 дополнительных условий.
б) Пространственная схема нагружения.
т.о. для пространственной схемы нагружения неизвестными являются не реакции, а составляющие реакций. При n амортизаторах имеем 3n неизвестных.
Из 6-ти уравнений определяем 6 неизвестных. Т.о. число дополнительных условий, которое необходимо задать 3n –6. Дополнительные условия получаем аналогично как и для схемы а). Итак, считаем, что нам известны либо реакции (для схемы а), либо составляющие реакций (схема б). На этом расчет закончен. Динамический расчет
1. Определение инерционных и жесткостных параметров системы. 1.1 Определение инерционных параметров. mi масса – инерционный параметр системы при поступательном движении; Ixx, Iyy, Izz – моменты инерции при поворотном движении; m – определяется суммирование масс различных частей, узлов, деталей блока.
Iii – собственный момент инерции всего блока относительного его центральных осей. Они определяются следующим образом:
1.2 Жесткостные параметры системы. Cg – суммарная жесткость системы (динамическая).
Представляется в виде суммы динамических жесткостей системы или поворотных жесткостей. Динамические жесткости амортизаторов определяются по графикам динамической жесткости.
Эти графики сняты экспериментально. А – амплитуда вибрации основания. Cgu – значение динамических жесткостей. Характер зависимости – линейный. График дается для трех значений: Pmin, Pmax, Pmin. Зная график зависимости и амплитуду вибрации основания, можно говорить об определении значений динамических жесткостей амортизаторов. Если графика нет, то Cg = 1,1 … 1,2 C, где С – статическая жесткость, определяемая по графику статической жесткости.
Динамическая жесткость системы определяется только через динамические жесткости амортизаторов и не может быть изменена при выбранном типоразмере амортизатора. Поворотная жесткость определяется еще и координатами установки амортизатора и может быть изменена за счет изменения этих координат.
1.3 Определение парциальных частот. Парциальные частоты определяются через инерционные и жесткостные параметры системы.
1.4 Определение собственных частот системы амортизации. Собственные частоты системы амортизации определяются через парциальные частоты с учетом наличия плоскостей симметрии.
1.5 Расчет коэффициента динамичности.
m - масса блока; kg - коэффициент демпфирования, который определяется по графику (график экспериментальный для различных нагрузок на амортизатор);
- сумма по всем амортизаторам по соответствующим индексам. В зарезонансной зоне можно принять так: В резонансной зоне Для уменьшения коэффициента динамичности в резонансной зоне необходимо увеличить Kg. Для этого в системе предусматривается максимальная связность перемещений, т.е. отсутствие плоскостей симметрии.
1.6 Определение ускорения объекта.
Ориентировочно оценку коэффициента динамичности можно вести по АЧХ амортизатора.
Замечание: jоб – ускорение центра тяжести объекта. В некоторых точках блока за счет поворотных движений ускорение может быть больше.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 1234; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.103.14 (0.012 с.) |



 - сила тяжести блока.
- сила тяжести блока.


 и
и  реакция P1 = P2 = … = Pn = G/n
реакция P1 = P2 = … = Pn = G/n




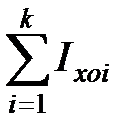 – сумма собственных моментов инерции элементарных блоков относительно центров координатных осей этих блоков. Учитывая, что блоки простейших форм, их моменты инерции рассчитываются по таблицам.
– сумма собственных моментов инерции элементарных блоков относительно центров координатных осей этих блоков. Учитывая, что блоки простейших форм, их моменты инерции рассчитываются по таблицам. – дополнительные моменты инерции, создаваемые блоком относительно координатных осей X, Y или Z.
– дополнительные моменты инерции, создаваемые блоком относительно координатных осей X, Y или Z.



 - собственная частота;
- собственная частота; - воздействующая частота;
- воздействующая частота;
 - в закрытой области.
- в закрытой области.

 – очень сильная зависимость.
– очень сильная зависимость.





