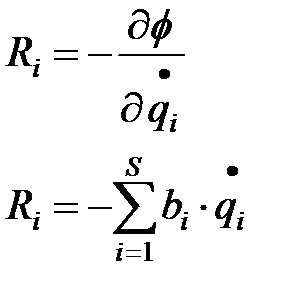Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные виды воздействующих факторов на рэа . Механичекие воздействия их основные виды и применения.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
8. Классификация внешних воздействий:
* Не кинематические ВВФ, а климатические ВВФ.
Механические и внешние воздействующие факторы: 1. Колебания: a. синусоидальная случайная вибрация; b. акустический шум (акустические воздействия характерны для ракетной и бортовой ЭВС, иногда для военной аппаратуры; начинается с c. качка (характеризуется амплитудой, частотой и периодом); d. крен, наклон. 2. Удар – кратковременное воздействие внешней силы: a. механический; b. удар при свободном падении; c. сейсмический удар; d. гидравлический удар; e. аэродинамический удар; f. баллистический удар. 3. Ускорение: a. линейные; b. угловые; c. центростремительные; d. невесомость. 4. Механическое давление: a. статическое; b. динамическое. 5. Сила: a. постоянная; b. переменная. 6. Момент и распределенный момент. 7. Поток жидкости: a. скорость течения; b. скоростной напор.
В процессе эксплуатации и транспортировки РЭА подвергается воздействию следующих механических сил: 1. Вибрация - периодические колебания элементов или конструкции в целом; 2. Удар - кратковременное воздействие внешней силы; 3. Центробежные и линейные ускорения; 4. Акустические воздействия.
Наиболее распространены 1 и 2 виды воздействий; 3-й вид воздействий может быть оценен путем статического расчета за счет суммирования существующих уже статических усилий (вес, ….) и возникающих за счет них ускорений.
Так как в случае 3 все сводится к статическому расчету, в данном курсе эти виды ускорений не рассматриваются. Если при расчете оказывается, что Акустические воздействия характерны для ракетной и бортовой РЭА, иногда для военной аппаратуры. Способы защиты от них особые и решаются индивидуальным порядком. В данном курсе не рассматриваются.
В связи с наличием данных воздействий, к РЭА предъявляются следующие требования:
Энергетические соотношения в системе виброизоляцииции. Уравнение Лагранжа
Допустим, существует система c S степенями свободы. 1. Кинематическая энергия системы «Т».
aij - инерционный (кинетический) параметр системы
2. Потенциальная энергия объекта «П».
Сij – жесткостной параметр системы: qi, qj – деформации упругих элементов (относительные). 3. Диссипативная функция «Ф».
bij – коэффициент демпфирования.
4. Уравнение Лагранжа (уравнение движения объекта).
I II III L=T-П - функция Лагранжа. i – число обобщенных координат, равное числу степеней свободы. I - баланс кинетической и потенциальной энергии в системе. II - потери энергии на диссипацию. III - приток энергии за счет возмущающих сил. В частных случаях Q(t) равно нулю: a) при свободном движении объекта (смещение блока от положения равновесия) b) кинематическое возмущение Данное уравнение позволяет проанализировать движение системы с любой степенью свободы и в любой момент времени. Для системы c S степенями свободы уравнение Лагранжа превращается в систему из S дифференциальных уравнений. При S=6 уравнение Лагранжа – система из 6-ти уравнений. Решение в общем виде подобной системы – сложная задача даже при использовании ЭВМ. При S = 1 - система решается. При S > 1 – применяются упрощенные методы расчета системы.
|
|||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 1329; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.137.244 (0.009 с.) |


 );
);
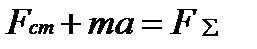
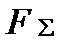 больше критического значения необходимо принимать соответствующие меры.
больше критического значения необходимо принимать соответствующие меры.
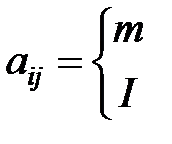

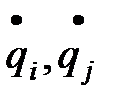 - обобщенные скорости по соответствующим координатам (скорости абсолютные).
- обобщенные скорости по соответствующим координатам (скорости абсолютные).