
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Жесткостные и инерционные параметры систем виброизоляцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
2. Определение инерционных и жесткостных параметров системы. 2.1 Определение инерционных параметров. mi масса – инерционный параметр системы при поступательном движении; Ixx, Iyy, Izz – моменты инерции при поворотном движении; m – определяется суммирование масс различных частей, узлов, деталей блока.
Iii – собственный момент инерции всего блока относительного его центральных осей. Они определяются следующим образом:
1.2 Жесткостные параметры системы. Cg – суммарная жесткость системы (динамическая).
Представляется в виде суммы динамических жесткостей системы или поворотных жесткостей. Динамические жесткости амортизаторов определяются по графикам динамической жесткости.
Эти графики сняты экспериментально. А – амплитуда вибрации основания. Cgu – значение динамических жесткостей. Характер зависимости – линейный. График дается для трех значений: Pmin, Pmax, Pmin. Зная график зависимости и амплитуду вибрации основания, можно говорить об определении значений динамических жесткостей амортизаторов. Если графика нет, то Cg = 1,1 … 1,2 C, где С – статическая жесткость, определяемая по графику статической жесткости.
Динамическая жесткость системы определяется только через динамические жесткости амортизаторов и не может быть изменена при выбранном типоразмере амортизатора. Поворотная жесткость определяется еще и координатами установки амортизатора и может быть изменена за счет изменения этих координат.
1.3 Определение парциальных частот. Парциальные частоты определяются через инерционные и жесткостные параметры системы.
1.7 Определение собственных частот системы амортизации. Собственные частоты системы амортизации определяются через парциальные частоты с учетом наличия плоскостей симметрии.
1.8 Расчет коэффициента динамичности.
m - масса блока; kg - коэффициент демпфирования, который определяется по графику (график экспериментальный для различных нагрузок на амортизатор);
- сумма по всем амортизаторам по соответствующим индексам. В зарезонансной зоне можно принять так: В резонансной зоне Для уменьшения коэффициента динамичности в резонансной зоне необходимо увеличить Kg. Для этого в системе предусматривается максимальная связность перемещений, т.е. отсутствие плоскостей симметрии.
1.9 Определение ускорения объекта.
Ориентировочно оценку коэффициента динамичности можно вести по АЧХ амортизатора.
Замечание: jоб – ускорение центра тяжести объекта. В некоторых точках блока за счет поворотных движений ускорение может быть больше. 23 Свободное движение блока на виброизоляторах, использующих силы вязкого трения. 1. Свободное движение объекта вязким трением с одной степенью свободы.
с - жесткостной параметр системы. а - инерционный параметр системы. Существуют два случая: 1. Малое затухание системы
Т.к. обычно
Примечания: a) b) Затухание практически не искажает значение собственной частоты. c) Затухание свободных колебаний происходит по экспоненте и амплитуда колебаний стремится к 0. Считают, что амплитуда колебаний равна 0 через 10…15 периодов собственных колебаний. 2. Значительные потери
Рассмотренные случаи соответствуют установке виброизоляторов с вязким трением или гистерезисными потерями, для которых справедлива функция:
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 602; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.101.219 (0.008 с.) |



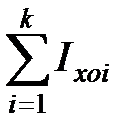 – сумма собственных моментов инерции элементарных блоков относительно центров координатных осей этих блоков. Учитывая, что блоки простейших форм, их моменты инерции рассчитываются по таблицам.
– сумма собственных моментов инерции элементарных блоков относительно центров координатных осей этих блоков. Учитывая, что блоки простейших форм, их моменты инерции рассчитываются по таблицам. – дополнительные моменты инерции, создаваемые блоком относительно координатных осей X, Y или Z.
– дополнительные моменты инерции, создаваемые блоком относительно координатных осей X, Y или Z.



 - собственная частота;
- собственная частота; - воздействующая частота;
- воздействующая частота;
 - в закрытой области.
- в закрытой области.

 – очень сильная зависимость.
– очень сильная зависимость.


 ,
, 
 ,
, 



 - коэффициент затухания.
- коэффициент затухания.

 q0 – начальное смещение.
q0 – начальное смещение.
 - угол отсечки.
- угол отсечки.
 на практике логарифмический декремент Колебаний:
на практике логарифмический декремент Колебаний: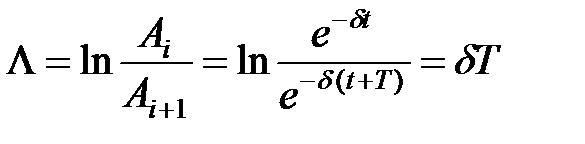
 . Характер движения апериодический. В системах виброизоляцииции практически не встречается.
. Характер движения апериодический. В системах виброизоляцииции практически не встречается.
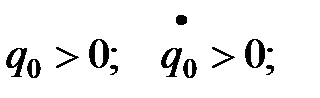 2.
2. 
 .
.


