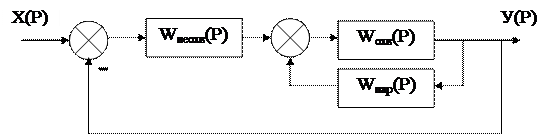Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
По передаточной функции замкнутой системы построим кривую переходного процесса (на эвм).Содержание книги
Поиск на нашем сайте
Передаточная функция замкнутой системы:
Таблица экспериментальных данных.
Кривая переходного процесса замкнутой системы, построенная по экспериментальным данным, полученным на ЭВМ.

        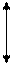    
1. 2. 2.1. 2.2. 2.3. 2.4. Определение основных показателей качества по кривой переходного процесса. 1. Максимальное динамическое отклонение – максимальная разность между заданными и действительными значениями регулируемой величины в переходном режиме. ∆max дин = hуст = 0,31 2. Максимальное перерегулирование – максимальное отклонение переходной характеристики от установившегося значения переходной величины, выраженное в относительных единицах.
Обычно σmax ≤ 20÷30%.
3. Колебательность процесса:
(определяется как отношение разности двух соседних амплитуд, направленных в одну сторону, к большей из них в относительных единицах) Для работоспособных систем ψ ≥ 75÷90%
4. Время регулирования – tрегул – минимальное время от начала нанесения возмущения до момента, когда регулируемая величина будет оставаться близкой к установившемуся значению с заданной точностью; т.е. |h(t) – hуст| ≤ ∆, где ∆ - постоянная величина, значение которой нужно оговаривать (обычно ∆=2÷5% hуст).
∆ = 0,0155 0,2945 ≤ h(t) ≤ 0,3255
Определим по графику время регулирования tрегул = 76.2 Вывод. Данная система автоматического регулирования не отвечает требуемым показателям качества, т.к. величина максимального перерегулирования составляет 74% и колебательность процесса равна 43%. Данная система в статике неработоспособна, т.к. имеет большую статическую ошибку равную 69%. Для того чтобы данная система была работоспособна в статике необходима уменьшить статическую ошибку. Для уменьшения статической ошибки необходима увеличить kраз.. Однако увеличение kраз. ведёт к уменьшению запаса устойчивости, поэтому увеличивать kраз. нужно очень осторожно.
РАЗДЕЛ №2 Синтез системы автоматического регулирования. Последовательная коррекция
При последовательной коррекции корректирующее звено включают в прямую цепь регулирования. Схема последовательной коррекции имеет вид:
При выборе последовательного корректирующего звена необходимо помнить, что дифференцирующие звенья увеличивают запас устойчивости системы и увеличивают ее быстродействие, интегрирующие – улучшают статику системы, но уменьшают запас устойчивости системы, безинерционные – уменьшают статическую ошибку системы (и, если К>1 и уменьшают при этом запас устойчивости системы). В данном случае, мне необходимо уменьшить статическую ошибку. При этом величина максимального перерегулирования не должна превысить 25%, колебательность должна быть больше 75%, а время регулирования не должно превышать 60с. Из этих соображений я выбираю безинерционное звено, тогда Wисх. (р) и Wпосл. (р) будут иметь вид:
Заменим Wисх. (р) и Wпосл. (р) на эквивалентную функцию Wск. (р)
Рассмотрим влияние этого звена на статику системы:
То есть введение безинерционного звена в прямую цепь регулирования уменьшает статическую ошибку до 0%. Влияние безинерционного звена на динамику рассмотрим с помощью АФЧХ скорректированной системы:
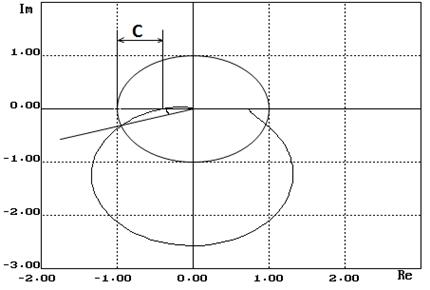
Таблица для построения годографа Найквиста.
Как видно из годографа Найквиста система имеет запас устойчивости по модулю равный 0.69 и запас устойчивости по фазе равный 86о. Теперь по передаточной функции замкнутой системы построим кривую переходного процесса (на ЭВМ) Передаточная функция замкнутой системы:
Построим для данной передаточной функции кривую переходного процесса по точкам, полученным из расчета на ЭВМ. Таблица экспериментальных данных.
Определение основных показателей качества по кривой переходного процесса. 1) Максимальное динамическое отклонение.
2) Время Регулирования
3) Величина максимального перерегулирования.
4) Колебательность процесса.
Вывод.
Применяя последовательную коррекцию к данной системе автоматического регулирования, и взяв в качестве корректирующего безинерционное звено, равное Параллельная коррекция. Структурная схема САР имеет вид:
Передаточная функция системы имеет вид:
В качестве охватываемого звена выбираем безинерционное звено, имеющее вид:
Тогда передаточная функция не охватываемого звена будет иметь:
1. 2. 2.1. Отрицательная жесткая обратная связь.
  В качестве параллельной функции выбираем В качестве параллельной функции выбираем
Таблица для построения годографа Найквиста.
Как видно из годографа Найквиста система имеет запас устойчивости по модулю равный 0,6 и запас устойчивости по фазе равный 17о. Таблица экспериментальных данных.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 385; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.164.200 (0.011 с.) |

 Построим для данной передаточной функции кривую переходного процесса по точкам, полученным из расчета на ЭВМ.
Построим для данной передаточной функции кривую переходного процесса по точкам, полученным из расчета на ЭВМ.


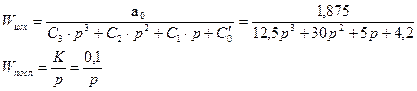

 ;
;








 , удалось уменьшить статическую ошибку до 0 (улучшить статику), увеличить запас устойчивости по фазе до 86о (улудшилась динамика). Теперь система отвечает требуемым показателям качества, т.к. величина максимального перерегулирования составляет 1%, колебательность процесса равна 100% и время максимального перерегулирования не превышает 60с. Данная система является в статике работоспособной и отвечает основным критериям в динамике.
, удалось уменьшить статическую ошибку до 0 (улучшить статику), увеличить запас устойчивости по фазе до 86о (улудшилась динамика). Теперь система отвечает требуемым показателям качества, т.к. величина максимального перерегулирования составляет 1%, колебательность процесса равна 100% и время максимального перерегулирования не превышает 60с. Данная система является в статике работоспособной и отвечает основным критериям в динамике.