
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение статизма системы.Содержание книги Поиск на нашем сайте
Для оценки качества системы в статике применяют относительную статическую ошибку – статизм, которую определяют как отношение абсолютной статической ошибки к заданному значению регулируемой величины.
Для работоспособной системы статизм не должен превышать (2 ¸ 5%). Данная система в статике неработоспособна, т. к. статизм равен 61%.
Исследование замкнутой системы на устойчивость с применением критериев Гурвица, Михайлова и Найквиста.
1. 2. Алгебраический критерий Гурвица. Алгебраический критерий устойчивости позволяет судить об устойчивости системы по коэффициентам характеристического уравнения. Система автоматического регулирования будет устойчива, если все коэффициенты её характеристического уравнения имеют одинаковые знаки, а главный диагональный определитель системы (определитель Гурвица) и его диагональные миноры будут положительными.
Передаточная функция замкнутой системы:
Характеристическое уравнение замкнутой системы:
Коэффициенты характеристического уравнения:
Главный диагональный определитель системы (определитель Гурвица):
Замкнутая система устойчива по Гурвицу, так как выполняются необходимые и достаточные условия устойчивости. Найдём значение границы устойчивости:
1. 2. 2.1. Частотный критерий Михайлова. Частотные критерии устойчивости позволяют судить об устойчивости систем автоматического управления по виду их частотных характеристик. САР устойчива, если при изменении частоты от 0 до ∞ годограф вектора ее характеристического уравнения (годограф Михайлова) проходит последовательно против часовой стрелки n квадрантов, не пропуская ни одного. Передаточная функция замкнутой системы:
Характеристическое уравнение замкнутой системы:
Коэффициенты характеристического уравнения:
Заменив в характеристическом уравнении оператор р на оператор jω, получим вектор Нзам(jω).
Найдем частоту
Найдем частоту
Таблица для построения годографа Михайлова.
Годограф Михайлова проходит через три квадранта, не пропуская ни одного, следовательно, система устойчива по Михайлову. Ширина годографа Михайлова: Re(0) – Re(w**)= 14,290 – (-1,650) = 15,94
1. 2. 2.1. 2.2. Частотный критерий Найквиста. Этот критерий позволяет судить об устойчивости замкнутых САР по амплитудно-фазовой характеристике разомкнутой САР. Замкнутая САР устойчива, если: · устойчива разомкнутая САР и её АФЧХ не охватывает точку с координатами (-1, j0); · не устойчива разомкнутая САР и её АФЧХ охватывает точку с координатами (-1, j0). Передаточная функция разомкнутой системы:
Амплитудо-фазо-частотная характеристика системы:
Найдем частоту w* при которой годограф Найквиста пересечет мнимую полуось.
Таблица для построения годографа Найквиста.
Замкнутая система устойчива (по Найквисту), т. к. устойчивая разомкнутая САР и её АФЧХ не охватывает точку с координатами (-1, j0).
Годограф Найквиста полученный на компьютере
1. 2. 2.1. 2.2. 1. 2. 2.1. 2.2. Определение запаса устойчивости замкнутой системы по модулю и фазе. Запас устойчивости по модулю определяется отрезком отрицательной действительной полуоси от точки В данном случае годограф Найквиста пересекает отрицательную действительную полуось:
Запас устойчивости по фазе определяется углом В данном случае годограф Найквиста пересекается с единичной окружностью, и следовательно:
1. 2. 2.1. 2.2. 2.3.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 984; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.188.241 (0.007 с.) |


 ;
;


 ;
;  ;
;  ;
;  ;
;

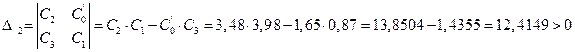
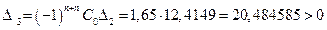
 выполняется первое условие (все коэффициенты характеристического уравнения имеют одинаковые знаки).
выполняется первое условие (все коэффициенты характеристического уравнения имеют одинаковые знаки). выполняется второе условие (диагональный определитель, составленный из коэффициентов характеристического уравнения и его диагональные миноры положительны).
выполняется второе условие (диагональный определитель, составленный из коэффициентов характеристического уравнения и его диагональные миноры положительны).



 ;
;  ;
;  ;
; 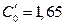



 при которой годограф Михайлова пересечет мнимую полуось.
при которой годограф Михайлова пересечет мнимую полуось.


 при которой годограф Михайлова пересечет действительную полуось.
при которой годограф Михайлова пересечет действительную полуось.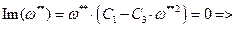









 ;
;




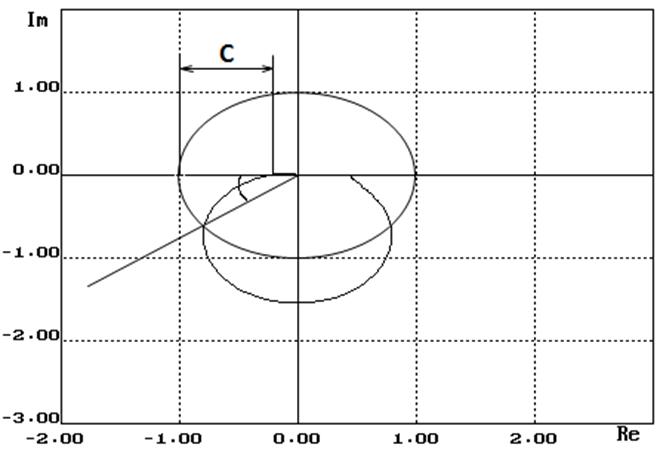
 до точки пересечения АФЧХ оси абсцисс.
до точки пересечения АФЧХ оси абсцисс.
 между отрицательной действительной полуосью и лучом, проведенным из начала координат в точку пересечения окружности единичного радиуса с АФЧХ разомкнутой системы
между отрицательной действительной полуосью и лучом, проведенным из начала координат в точку пересечения окружности единичного радиуса с АФЧХ разомкнутой системы



