
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Анализ системы автоматического регулирования.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте ПОЯСНИТЕЛЬНАЯ ЗАПИСКА к курсовому проекту (работе) по ____________________________________ наименование учебной дисциплины на тему:_________________________________________________________ ________________________________________________________________ Автор проекта (работы)____________________________________________ подпись, дата, инициалы, фамилия Специальность ___________________________________________________ номер, наименование Обозначение курсового проекта (работы) _________Группа______________ Руководитель проекта _________________ __________________________ подпись, дата инициалы, фамилия
Проект (работа) защищен (а) ___________ Оценка________________
Члены комиссии: ______________________ ________________ подпись, дата инициалы, фамилия
______________________ ________________ подпись, дата инициалы, фамилия
______________________ ________________ подпись, дата инициалы, фамилия г. Тверь, 2007 ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ТВЕРСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» (ГОУВПО «ТГТУ»)
Кафедра ЭВМ
ЗАДАНИЕ НА КУРСОВОЙ ПРОЕКТ (РАБОТУ)
Студент____________________________ код________ группа ___________ фамилия, инициалы 1.Тема __________________________________________________________ ________________________________________________________________ 2. Срок представления проекта (работы) к защите "____"__________2007 г. 3. Исходные данные для проектирования (научного исследования) ________________________________________________________________________________________________________________________________ 4. Содержание пояснительной записки курсового проекта (работы) 4.1._____________________________________________________________ 4.2._____________________________________________________________ 4.3._____________________________________________________________ 4.4._____________________________________________________________ 4..._____________________________________________________________ 5. Перечень графического материала: ________________________________ ________________________________________________________________
Руководитель проекта (работы) ________________ _________________ подпись, дата инициалы, фамилия
Задание принял к исполнению ____________ "___"______2007 г. подпись
Содержание Оглавление Задание. 4 I. Анализ системы автоматического регулирования. 4 II. Синтез системы автоматического регулирования. 4 РАЗДЕЛ №1 Анализ системы автоматического регулирования. 4 1. Структурные преобразования. 4 1.1.Приведение системы к одноконтурной, определение числовых значений параметров САР. 4 1.2. Передаточные функции разомкнутой и замкнутой систем. 4 1.3. Определение статизма системы. 4 2. Исследование замкнутой системы на устойчивость с применением критериев Гурвица, Михайлова и Найквиста. 4 2.1. Алгебраический критерий Гурвица. 4 2.2. Частотный критерий Михайлова. 4 2.3. Частотный критерий Найквиста. 4 2.4. По передаточной функции замкнутой системы построим кривую переходного процесса 4 РАЗДЕЛ №2 Синтез системы автоматического регулирования. 4 1. Последовательная коррекция. 4 2. Параллельная коррекция. 4 2.1. Отрицательная жесткая обратная связь. 4 2.2. Положительная гибкая обратная связь. 4 2.3. Отрицательная гибкая обратная связь. 4
Задание
I. Анализ системы автоматического регулирования.
Исходные данные. 1. Структурная схема исследуемой САР
2. Передаточные функции звеньев САР (табл.1). Таблица №1
3. Параметры звеньев (передаточные коэффициенты и постоянные времени) (табл.2). Таблица №2
Требуется: 1. Провести структурное преобразование САР, превратив систему в одноконтурную. При этом звенья САР, охваченные местными обратными связями, заменить эквивалентными звеньями и определить для них передаточные функции. Определить числовые значения параметров эквивалентных звеньев. 2. По передаточным функциям звеньев одноконтурных САР определить передаточные функции и характеристические уравнения разомкнутой и замкнутой систем. 3. Определить передаточный коэффициент системы и статизм системы. 4. Исследовать замкнутую систему на устойчивость при помощи критерия устойчивости Гурвица. Определить значение критического коэффициента усиления системы. Если замкнутая САР неустойчива, то изменив значение одного (или обоих) коэффициентов обратных связей (β1, β2) или значение одного из коэффициентов усиления звеньев (к1, к2, к3) добиться ее устойчивости. 5. Скорректированную (исходную, если система устойчива) систему исследовать на устойчивость частотными критериями Михайлова и Найквиста. По критерию Михайлова найти значение критического коэффициента усиления системы, по критерию Найквиста определить запас устойчивости замкнутой САР по модулю и фазе. 6. На основании математического описания системы построить кривую переходного процесса замкнутой САР. Для расчета кривой переходного процесса на ЭВМ целесообразно воспользоваться программным средством «ТАУ». 7. По кривой переходного процесса определить основные показатели качества: время регулирования – tрег, величину перерегулирования – σmax, колебательность процесса – ψ, и сделать вывод, отвечает исследуемая САР требуемым показателям качества (σmax ≤ 20%, ψ ≥ 75 ÷ 90%) или нет.
II. Синтез системы автоматического регулирования.
Исходные данные: 1. Структурная схема одноконтурной САР, полученная в разделе I. 2. Переходная характеристика исследованной замкнутой САР и показатели ее качества (коэффициент статизма, время регулирования – tрег, перерегулирование – σmax и колебательность процесса – ψ).
Требуется:
1. Ввести в исследуемую систему последовательное корректирующее звено по схеме (рис.1.):
Wисх(P) – передаточная функция исходной разомкнутой системы; Wпосл(P) – передаточная функция вводимого корректирующего звена.
Рис.1. Схема последовательной коррекции
Введение корректирующего звена должно обеспечить статическую ошибку системы (коэффициент статизма) ≤ 2 ÷ 5%, колебательность переходного процесса ψ ≥ 75 ÷ 90%, а время регулирования tрег меньше 20с
2. Изучить влияние местной обратной связи (параллельного корректи-рующего звена) на динамику и статику системы. С этой целью привести исследуемую САР к виду на рис.2.:
Рис.2. Схема параллельной коррекции
При этом передаточную функцию исходной разомкнутой системы представить в виде: Wисх(P)= Wнеохв(P)•Wохв(P),
где: Wохв(P) – передаточная функция звеньев, охватываемых местной обратной связью; Wохв(P) – передаточная функция остальных звеньев исходной системы; Wпар(P) – передаточная функция корректирующего звена.
В качестве охватываемых выбирать инерционные и интегрирующие звенья.
а) В качестве Wпар(P) выбрать безинерционное звено (жесткая отрицательная обратная связь):
Wпар(P) = -кос, где 1< кос<5,
и изучить его влияние на статику и динамику системы. б) Ввести гибкую обратную связь (положительную и отрицательную) и изучить ее влияние на статику и динамику системы:
где 1< кос<5, T ≤ кос . По результатам синтеза САР сделать выводы. РАЗДЕЛ №1 1.1. 1.2. Передаточные функции разомкнутой и замкнутой систем. Передаточная функция разомкнутой системы:
Передаточная функция замкнутой системы:
Числовые коэффициенты:
Подставляя числовые значения, получим передаточную функцию Wраз(p) равную:
Подставляя числовые значения, получим передаточную функцию Wзам(p) равную:
2.1. 2.1. 2.2. 2.1. 2.2. 1. 2. 2.1. 2.2. 2.1. 2.2. 2.3. 2.1. 2.2. 2.3. 2.4. Вывод. Данная система автоматического регулирования не отвечает требуемым показателям качества, т.к. величина максимального перерегулирования составляет 74% и колебательность процесса равна 43%. Данная система в статике неработоспособна, т.к. имеет большую статическую ошибку равную 69%. Для того чтобы данная система была работоспособна в статике необходима уменьшить статическую ошибку. Для уменьшения статической ошибки необходима увеличить kраз.. Однако увеличение kраз. ведёт к уменьшению запаса устойчивости, поэтому увеличивать kраз. нужно очень осторожно. РАЗДЕЛ №2 Последовательная коррекция
При последовательной коррекции корректирующее звено включают в прямую цепь регулирования. Схема последовательной коррекции имеет вид:
При выборе последовательного корректирующего звена необходимо помнить, что дифференцирующие звенья увеличивают запас устойчивости системы и увеличивают ее быстродействие, интегрирующие – улучшают статику системы, но уменьшают запас устойчивости системы, безинерционные – уменьшают статическую ошибку системы (и, если К>1 и уменьшают при этом запас устойчивости системы). В данном случае, мне необходимо уменьшить статическую ошибку. При этом величина максимального перерегулирования не должна превысить 25%, колебательность должна быть больше 75%, а время регулирования не должно превышать 60с. Из этих соображений я выбираю безинерционное звено, тогда Wисх. (р) и Wпосл. (р) будут иметь вид:
Заменим Wисх. (р) и Wпосл. (р) на эквивалентную функцию Wск. (р)
Рассмотрим влияние этого звена на статику системы:
То есть введение безинерционного звена в прямую цепь регулирования уменьшает статическую ошибку до 0%. Влияние безинерционного звена на динамику рассмотрим с помощью АФЧХ скорректированной системы:
Таблица для построения годографа Найквиста.
Как видно из годографа Найквиста система имеет запас устойчивости по модулю равный 0.69 и запас устойчивости по фазе равный 86о. Теперь по передаточной функции замкнутой системы построим кривую переходного процесса (на ЭВМ) Передаточная функция замкнутой системы:
Построим для данной передаточной функции кривую переходного процесса по точкам, полученным из расчета на ЭВМ. Таблица экспериментальных данных.
Вывод. Применяя последовательную коррекцию к данной системе автоматического регулирования, и взяв в качестве корректирующего безинерционное звено, равное Параллельная коррекция. Структурная схема САР имеет вид:
Передаточная функция системы имеет вид:
В качестве охватываемого звена выбираем безинерционное звено, имеющее вид:
Тогда передаточная функция не охватываемого звена будет иметь:
1. 2. 2.1. Отрицательная жесткая обратная связь.
  В качестве параллельной функции выбираем В качестве параллельной функции выбираем
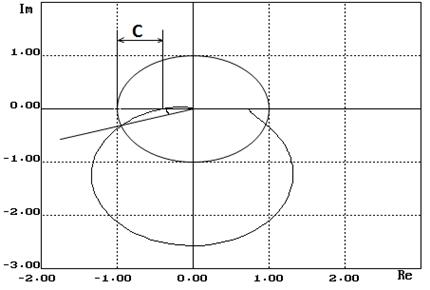
Таблица для построения годографа Найквиста.
Как видно из годографа Найквиста система имеет запас устойчивости по модулю равный 0,6 и запас устойчивости по фазе равный 17о. Таблица экспериментальных данных.
2.1. ПОЯСНИТЕЛЬНАЯ ЗАПИСКА к курсовому проекту (работе) по ____________________________________ наименование учебной дисциплины на тему:_________________________________________________________ ________________________________________________________________ Автор проекта (работы)____________________________________________ подпись, дата, инициалы, фамилия Специальность ___________________________________________________ номер, наименование Обозначение курсового проекта (работы) _________Группа______________ Руководитель проекта _________________ __________________________ подпись, дата инициалы, фамилия
Проект (работа) защищен (а) ___________ Оценка________________
Члены комиссии: ______________________ ________________ подпись, дата инициалы, фамилия
______________________ ________________ подпись, дата инициалы, фамилия
______________________ ________________ подпись, дата инициалы, фамилия г. Тверь, 2007 ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ТВЕРСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» (ГОУВПО «ТГТУ»)
Кафедра ЭВМ
ЗАДАНИЕ НА КУРСОВОЙ ПРОЕКТ (РАБОТУ)
Студент____________________________ код________ группа ___________ фамилия, инициалы 1.Тема __________________________________________________________ ________________________________________________________________ 2. Срок представления проекта (работы) к защите "____"__________2007 г. 3. Исходные данные для проектирования (научного исследования) ________________________________________________________________________________________________________________________________ 4. Содержание пояснительной записки курсового проекта (работы) 4.1._____________________________________________________________ 4.2._____________________________________________________________ 4.3._____________________________________________________________ 4.4._____________________________________________________________ 4..._____________________________________________________________ 5. Перечень графического материала: ________________________________ ________________________________________________________________
Руководитель проекта (работы) ________________ _________________ подпись, дата инициалы, фамилия
Задание принял к исполнению ____________ "___"______2007 г. подпись
Содержание Оглавление Задание. 4 I. Анализ системы автоматического регулирования. 4 II. Синтез системы автоматического регулирования. 4 РАЗДЕЛ №1 Анализ системы автоматического регулирования. 4 1. Структурные преобразования. 4 1.1.Приведение системы к одноконтурной, определение числовых значений параметров САР. 4 1.2. Передаточные функции разомкнутой и замкнутой систем. 4 1.3. Определение статизма системы. 4 2. Исследование замкнутой системы на устойчивость с применением критериев Гурвица, Михайлова и Найквиста. 4 2.1. Алгебраический критерий Гурвица. 4 2.2. Частотный критерий Михайлова. 4 2.3. Частотный критерий Найквиста. 4 2.4. По передаточной функции замкнутой системы построим кривую переходного процесса 4 РАЗДЕЛ №2 Синтез системы автоматического регулирования. 4 1. Последовательная коррекция. 4 2. Параллельная коррекция. 4 2.1. Отрицательная жесткая обратная связь. 4 2.2. Положительная гибкая обратная связь. 4 2.3. Отрицательная гибкая обратная связь. 4
Задание
I. Анализ системы автоматического регулирования.
Исходные данные. 1. Структурная схема исследуемой САР
2. Передаточные функции звеньев САР (табл.1). Таблица №1
3. Параметры звеньев (передаточные коэффициенты и постоянные времени) (табл.2). Таблица №2
Требуется: 1. Провести структурное преобразование САР, превратив систему в одноконтурную. При этом звенья САР, охваченные местными обратными связями, заменить эквивалентными звеньями и определить для них передаточные функции. Определить числовые значения параметров эквивалентных звеньев. 2. По передаточным функциям звеньев одноконтурных САР определить передаточные функции и характеристические уравнения разомкнутой и замкнутой систем. 3. Определить передаточный коэффициент системы и статизм системы. 4. Исследовать замкнутую систему на устойчивость при помощи критерия устойчивости Гурвица. Определить значение критического коэффициента усиления системы. Если замкнутая САР неустойчива, то изменив значение одного (или обоих) коэффициентов обратных связей (β1, β2) или значение одного из коэффициентов усиления звеньев (к1, к2, к3) добиться ее устойчивости. 5. Скорректированную (исходную, если система устойчива) систему исследовать на устойчивость частотными критериями Михайлова и Найквиста. По критерию Михайлова найти значение критического коэффициента усиления системы, по критерию Найквиста определить запас устойчивости замкнутой САР по модулю и фазе. 6. На основании математического описания системы построить кривую переходного процесса замкнутой САР. Для расчета кривой переходного процесса на ЭВМ целесообразно воспользоваться программным средством «ТАУ». 7. По кривой переходного процесса определить основные показатели качества: время регулирования – tрег, величину перерегулирования – σmax, колебательность процесса – ψ, и сделать вывод, отвечает исследуемая САР требуемым показателям качества (σmax ≤ 20%, ψ ≥ 75 ÷ 90%) или нет.
II. Синтез системы автоматического регулирования.
Исходные данные: 1. Структурная схема одноконтурной САР, полученная в разделе I. 2. Переходная характеристика исследованной замкнутой САР и показатели ее качества (коэффициент статизма, время регулирования – tрег, перерегулирование – σmax и колебательность процесса – ψ).
Требуется:
1. Ввести в исследуемую систему последовательное корректирующее звено по схеме (рис.1.):
Wисх(P) – передаточная функция исходной разомкнутой системы; Wпосл(P) – передаточная функция вводимого корректирующего звена.
Рис.1. Схема последовательной коррекции
Введение корректирующего звена должно обеспечить статическую ошибку системы (коэффициент статизма) ≤ 2 ÷ 5%, колебательность переходного процесса ψ ≥ 75 ÷ 90%, а время регулирования tрег меньше 20с
2. Изучить влияние местной обратной связи (параллельного корректи-рующего звена) на динамику и статику системы. С этой целью привести исследуемую САР к виду на рис.2.:
Рис.2. Схема параллельной коррекции
При этом передаточную функцию исходной разомкнутой системы представить в виде: Wисх(P)= Wнеохв(P)•Wохв(P),
где: Wохв(P) – передаточная функция звеньев, охватываемых местной обратной связью; Wохв(P) – передаточная функция остальных звеньев исходной системы; Wпар(P) – передаточная функция корректирующего звена.
В качестве охватываемых выбирать инерционные и интегрирующие звенья.
а) В качестве Wпар(P) выбрать безинерционное звено (жесткая отрицательная обратная связь):
Wпар(P) = -кос, где 1< кос<5,
и изучить его влияние на статику и динамику системы. б) Ввести гибкую обратную связь (положительную и отрицательную) и изучить ее влияние на статику и динамику системы:
где 1< кос<5, T ≤ кос . По результатам синтеза САР сделать выводы. РАЗДЕЛ №1 Анализ системы автоматического регулирования. 1. Структурные преобразования.
1.1. Приведение системы к одноконтурной, определение числовых значений параметров САР. Структурное преобразование системы необходимо начать с преобразования звена с передаточной характеристикой W1(p) и соответствующим коэффициентом обратной связи β1. Это объединение на структурной схеме, приведенной ниже, и изображено пунктирной линией. Передаточную характеристику преобразованного звена назовем Wэкв1(p).
Так как звено с передаточной характеристикой Wэкв1(p) является встречно параллельным, то передаточная характеристика будет определяться выражением:
Тогда передаточная характеристика Wэкв1(p) равна:
Теперь соединим последовательно звенья с передаточными функциями W2(p) и W3 (p), а после, преобразуем встречно параллельное соединение передаточной функции Wэкв2(p) и коэффициента обратной связи β2. Это объединение на структурной схеме, приведенной ниже, и изображено пунктирной линией. Передаточную характеристику преобразованного звена назовем Wэкв2(p).
Передаточную характеристику преобразованного звена Wэкв2(p) определим как произведение передаточных функций Wэкв1(p) и W2(p).
Подставляя числовые значения, получим значения передаточных функций Wэкв1(p), Wэкв2(p):
После преобразования структурная схема системы приобретёт вид, который приведен ниже.
Теперь следует объединить звенья с передаточными характеристиками Wэкв1(p) и Wэкв2(p) в одно звено с передаточной характеристикой Wэкв(p). Это объединение будет являться заключительным, приводящим данную систему к одноконтурной, а значит передаточная характеристика Wэкв(p) будет являться передаточной функцией всей системы. На структурной схеме, приведенной ниже, это объединение изображено пунктирной линией.
Так как звенья располагаются последовательно, то их передаточная функция определяется как произведение передаточных функций звеньев.
1. 1.1. 1.2. Передаточные функции разомкнутой и замкнутой систем. Передаточная функция разомкнутой системы:
Передаточная функция замкнутой системы:
Числовые коэффициенты:
Подставляя числовые значения, получим передаточную функцию Wраз(p) равную:
Подставляя числовые значения, получим передаточную функцию Wзам(p) равную:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 709; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.009 с.) |







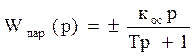 ,
,






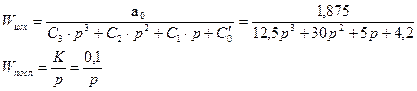

 ;
;




 , удалось уменьшить статическую ошибку до 0 (улучшить статику), увеличить запас устойчивости по фазе до 86о (улудшилась динамика). Теперь система отвечает требуемым показателям качества, т.к. величина максимального перерегулирования составляет 1%, колебательность процесса равна 100% и время максимального перерегулирования не превышает 60с. Данная система является в статике работоспособной и отвечает основным критериям в динамике.
, удалось уменьшить статическую ошибку до 0 (улучшить статику), увеличить запас устойчивости по фазе до 86о (улудшилась динамика). Теперь система отвечает требуемым показателям качества, т.к. величина максимального перерегулирования составляет 1%, колебательность процесса равна 100% и время максимального перерегулирования не превышает 60с. Данная система является в статике работоспособной и отвечает основным критериям в динамике.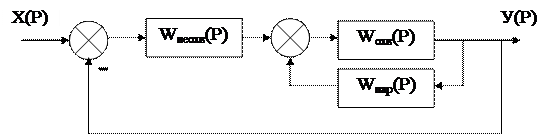







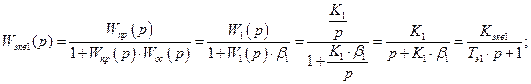


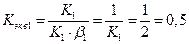











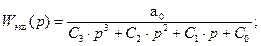



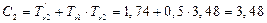
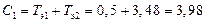
 .
.



