
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теория автоматического управленияСодержание книги Поиск на нашем сайте
ТЕОРИЯ автоматического УПРАВЛЕНИЯ Рабочая программа, методические указания и контрольные задания для студентов специальности 220301 «Автоматизация технологических процессов и производств (в нефтегазовой отрасли)»
Томск 2013 УДК 681.5
Теория автоматического управления: рабочая программа, метод. указания и контр. задания для студентов спец. 220301 «Автоматизация технологических процессов и производств (в нефтегазовой отрасли)» ИДО / Сост.
Рабочая программа, методические указания и контрольные задания рассмотрены и рекомендованы к изданию методическим семинаром кафедры интегрированных компьютерных систем управления
Зав. кафедрой ИКСУ, доцент, к. т. н. ______________ А. В. Лиепиньш
Аннотация Рабочая программа, методические указания и контрольные задания по дисциплине «Теория автоматического управления» предназначены для студентов специальности 220301 «Автоматизация технологических процессов и производств (в нефтегазовой отрасли)». Данная дисциплина изучается два семестра. Приведено содержание основных тем дисциплины, указаны перечень лабораторных работ и темы практических занятий. Приведены варианты заданий для контрольной работы и курсовой работы. Даны методические указания по выполнению контрольной и курсовой работ.
1.1. Цель преподавания дисциплины Курс «Теория автоматического управления» включен в учебные планы с целью усвоения студентами современных знаний по теории автоматического управления, принципов построения и методов исследования систем автоматического управления (САУ) и подготовки студентов к практической деятельности по проектированию, разработке, исследованию и эксплуатации систем этого класса. 1.2. Задачи изучения дисциплины Успешно изучивший дисциплину «Теория автоматического управления» студент должен иметь представление: · об основных принципах управления и тенденциях развития систем управления техническими объектами и их элементной базы; · о принципах математического и имитационного моделирования автоматических систем управления; знать и уметь использовать: · классификацию систем управления; их модели и основные характеристики; · методы анализа и синтеза систем автоматического управления; · средства вычислительной техники и численные методы для решения задач анализа и синтеза систем управления; · методы расчетов статических и динамических характеристик функциональных устройств систем автоматического управления; иметь опыт: · создания и реализации моделей САУ и их исследования; · использования систем автоматизированного проектирования и исследования современных систем управления; · использования пакетов прикладных программ по моделированию и расчету линейных и нелинейных моделей автоматических систем; · экспериментальных исследований автоматических и автоматизированных систем управления; · чтения и анализа основных типов схем систем автоматического управления. Вышеуказанные цели преподавания и задачи изучения дисциплины «Теория автоматического управления» достигаются за счет совместной с преподавателями и другими студентами, а также индивидуальной познавательной деятельности студентов. С этой целью используется полный набор современных способов и средств обучения: лекции, лабораторные и практические занятия, самостоятельная работа студентов по курсу; персональные ЭВМ и специальное лабораторное оборудование; учебники, учебные пособия, автоматизированные обучающие системы и методические указания к лабораторным работам и практическим занятиям; комплекты контрольных заданий для проверки знаний студентов и другие методические разработки обеспечивающей данный курс кафедры ИКСУ и других вузов страны. Практические навыки при изучении «Теории автоматического управления» студент приобретает во время практических занятий, при выполнении лабораторных работ, контрольной и курсовой работ. 1.3. Перечень дисциплин, усвоение которых студентами необходимо Учебный материал данной дисциплины базируется на знаниях, полученных студентами в курсах «Математические основы кибернетики», «Высшая математика», «Программное обеспечение персональных ЭВМ», а также на знаниях из таких естественно - научных и общетехнических дисциплин, как «Физика», «Теоретическая электротехника», «Теоретическая механика». СОДЕРЖАНИЕ ТЕОРЕТИЧЕСКОГО РАЗДЕЛА ДИСЦИПЛИНЫ Седьмой семестр Введение Предмет и задачи курса, его связь с другими дисциплинами. Роль теории управления в решении задач автоматизации технических объектов, технологических линий и автономных технических систем. 2.2. Основные понятия, определения Автоматические устройства и системы, их классификация по назначению. Управляемые объекты и их классификация. Управляемые величины, управляющие и возмущающие воздействия в объектах управления. Обобщенная структурная схема систем управления. Типовые задачи автоматического управления и регулирования: автоматическая стабилизация, программное управление, автоматическое слежение, экстремальное регулирование. Основные принципы построения САУ. Управления жесткое, по возмущению, по отклонению, адаптивное; сферы их применения и сопоставительный анализ. Классификация систем управления. Системы прямого и непрямого управления, непрерывного и дискретного действия, одномерные и многомерные по входам и выходам. Системы связанного и несвязанного управления. Обыкновенные, адаптивные и игровые системы. Методические указания Системы автоматического управления (САУ) являются сложными техническими объектами, которые могут иметь разнообразные функциональные назначения, различные принципы действия, исполнения и т. д. Поэтому для классификации САУ приходится использовать разнообразные критерии, позволяющие выделить те свойства систем, которые представляют наибольший интерес в определенных условиях или задачах. Среди многообразия классификационных признаков следует выделить два важнейших: · непрерывность (дискретность) сигналов в системе; · линейность (нелинейность) связи между входным и выходным сигналами элементов системы. Первый из этих признаков делит все системы на непрерывные, дискретные и релейные. Непрерывная система характеризуется тем, что все элементы, входящие в систему, имеют непрерывные выходные сигналы при подаче на их вход непрерывных во времени сигналов. В дискретной системе выходной сигнал хотя бы одного звена имеет вид импульсов при подаче на его вход непрерывного сигнала. Наконец, в системах релейного действия имеется хотя бы одно звено, сигнал на выходе которого изменяется скачком при непрерывном входном сигнале. По литературе ознакомиться с примерами систем непрерывного, дискретного и релейного действия. На этой основе желательно придумать свои примеры. Второй из выделенных признаков разделяет все системы (точнее, их математические модели) на два больших класса: линейные и нелинейные. Линейной система называется тогда, когда она описывается линейными уравнениями (алгебраическими, дифференциальными или разностными). Пусть некоторая система описывается уравнением
Первое соотношение означает, что в линейной системе реакция на сумму сигналов равна сумме реакций на отдельные сигналы. Из второго следует, что при изменении входного сигнала в
а оператор Следует обратить особое внимание на выделение систем стабилизации, программного управления и следящих систем, т.к. они построены по принципу обратной связи и поэтому имеют высокие качественные показатели.
2.2.2. Контрольные вопросы 1. Как называется автоматический регулятор совместно с объектом регулирования? 2. Как называется система автоматического регулирования, предназначенная для поддержания постоянной выходной величины? 3. Как называется система автоматического регулирования, выходная величина которой изменяется по заранее определенному закону? 4. Как изменяется во времени входной сигнал следящей системы (остается постоянным; изменяется по закону, который заранее известен; изменяется по закону, который заранее не известен)? 5. Определите назначение следящей системы. 6. В чем отличие системы непрерывного действия от дискретной системы? 7. Линейным или непрерывным является звено, описываемое уравнением 2.3. Математические модели и типовые характеристики Возможные виды математических моделей элементов и систем управления. Непрерывные и дискретные; линейные и нелинейные; стационарные и нестационарные; статические и динамические; детерминированные и стохастические математические модели. Типовые математические модели состояний и процессов в элементах и системах управления в форме «вход – выход»; в форме «вход – состояние – выход». Преобразование моделей. Методические указания Этот раздел по-прежнему связан с классификацией САУ. Однако она проводится на более глубоком уровне – на уровне математических описаний систем, которые принято называть математическими моделями. Следует обратить внимание на два вида моделей: в форме передаточных функций и в форме уравнений состояния (систем дифференциальных уравнений первого порядка). Используя сведения из курса «Математические основы кибернетики», обобщите понятия временных и частотных характеристик, которые также являются моделями звеньев и систем, на обыкновенные линейные стационарные САУ. 2.3.2. Контрольные вопросы 1. Чем отличаются дифференциальные уравнения стационарной и нестационарной систем? 2. Как получить статическую модель системы по ее дифференциальному уравнению? 3. Как осуществляется переход от модели САУ в форме передаточной функции к описанию уравнений состояния? 4. Какова будет размерность матрицы состояния, если передаточная функция системы имеет порядок 5. Для линейной стационарной системы, имеющей Методические указания Следует знать основные понятия, определяющие фундаментальные свойства объектов и систем управления. В практическом плане важнейшим свойством является устойчивость САУ. Поэтому следует знать понятие устойчивости, физическое содержание этого свойства, методы и меры его оценивания. Обратите внимание на практические способы оценивания устойчивости систем – по расположению полюсов замкнутой системы и по частотным характеристикам. Важно знать и уметь оценивать запасы устойчивости, что позволяет сравнивать различные варианты расчетов САУ при проектировании. 2.4.2. Контрольные вопросы 1. О какой устойчивости состояний или процессов в нелинейной САУ можно судить по корням характеристического уравнения ее линеаризованной модели (в малом, в большом, в целом)? 2. Какое математическое выражение из состава дифференциального уравнения системы 3. Вынужденная или свободная составляющая решения дифференциального уравнения системы используется для анализа ее устойчивости? 4. Что можно сказать об устойчивости системы, если характеристический полином ее линеаризованной модели содержит нулевой корень? 5. Устойчива ли САУ второго порядка, если все коэффициенты ее характеристического уравнения положительны? 6. Будет уменьшаться или увеличиваться запас устойчивости САУ при увеличении коэффициента передачи устойчивой в разомкнутом состоянии системы? 7. Определите значения коэффициента передачи
Методические указания В этом разделе изучаются установившиеся режимы в системах управления. Режимы подразделяют на два вида в зависимости от свойств выходного сигнала Если Режим второго вида устанавливается в устойчивой системе при подаче на ее вход сигнала, не отвечающего условию Выделенные два режима имеют важное прикладное значение. При рассмотрении первого режима оценивают величину статической ошибки, которая и является мерой точности в статике. Однако чаще приходится решать обратную задачу: по заданной величине статической ошибки находят значения коэффициента передачи регулятора, при которых ошибка не будет превышать заданного значения. Нужно знать содержание этих задач и уметь их решать, в том числе получая решения, обеспечивающие нулевую статическую погрешность в так называемых астатических системах. Динамические установившиеся режимы также рассматриваются в прямых и обратных задачах. Прямые задачи позволяют, например, оценить ошибки по скорости движения, по ускорению, используя полиноминальные воздействия. Применение гармонических воздействий дает возможность найти максимальную величину ошибки в виде амплитуды установившихся колебаний. Обратные задачи решаются на этапе проектирования САУ, позволяя найти значение коэффициента передачи регулятора, при котором та или иная ошибка не превосходит заданного значения. Следует уметь решать прямую и обратную задачи в случае установившегося динамического режима. 2.5.2. Контрольные вопросы 1. Уменьшится ли величина статической ошибки при увеличении коэффициента передачи регулятора? Поясните ответ решением задачи на примере приведенной системы.
Рис. 2.1 2. Какое условие при размещении интегрирующего звена в прямом канале нужно выполнить, чтобы статическая ошибка за счет влияния возмущения была бы равна нулю? 3. Чему равно установившееся значение выходного сигнала y(t) системы (см. вопрос 1), если а) 4. Чему равен выходной сигнал 5. Чему равна амплитуда ошибки 6. Определите величину статической ошибки в системе (см. вопрос 1), если 7. Запишите выражение для передаточной функции
Рис. 2.2 Методические указания При изучении этого раздела следует обратить внимание на методы определения переходной функции системы: аналитическое решение дифференциальных уравнений, использование операторного метода, моделирование на ЭВМ. В рамках последующих практических занятий нужно будет ознакомиться с программными реализациями некоторых методов и их вариантов. Переходные характеристики являются одной из основных типовых форм, позволяющих сравнивать системы одинакового назначения и выделять среди них лучшие. Практически удобно сопоставлять не сами характеристики, а их ключевые параметры, которые можно оценить количественно. Например, перерегулирование, длительность переходного процесса и др. Эти и другие параметры получили название показателей качества: они могут быть определены не только прямым путем непосредственно по переходной характеристике, но и косвенно – по частотным характеристикам, расположению корней и т.д. На этом основании выделяют прямые и косвенные показатели качества, используя их для сравнения систем. Нужно знать обе группы показателей и уметь их определять. 2.6.2. Контрольные вопросы 1. Определить примерные значения перерегулирования
Рис. 2.3 2. Какие корни характеристического уравнения системы (мнимые, вещественные, комплексно-сопряженные) будут ближайшими к мнимой оси, если переходная характеристика системы имеет представленный в вопросе 1 вид? 3. Какой обычно принимают величину D -зоны, выделенной на рисунке вопроса 1? 4. Какое из значений 5. Найдите примерное значение длительности переходного процесса в системе, имеющей лишь вещественные корни, из которых 2.7. Синтез систем автоматического управления Основные этапы синтеза САУ. Выбор принципов управления и алгоритмов управляющих устройств. Типовые регуляторы и их применение в САУ. Синтез типовых регуляторов и корректирующих устройств по логарифмическим частотным характеристикам. Модальный синтез линейных систем автоматического управления и условия его разрешимости. Алгоритмы модального синтеза и их характеристика. Пакеты прикладных программ для автоматизации синтеза САУ. Методические указания Синтез систем является основной задачей в построении САУ. Поэтому необходимо знать подходы к ее решению, уметь решать ее. Можно выделить два основных условия достижения цели. Необходимо, во-первых, знать принципы построения систем (принципы управления) и способы коррекции свойств САУ и, во-вторых, знать методы расчета параметров корректирующих элементов, вводимых в систему. Начальные сведения по первому из условий были получены при изучении раздела 2.2. В настоящем разделе предусмотрено их развитие. Оно связано с изучением устройств коррекции, вводимых последовательно, параллельно или в виде обратных связей, с выявлением их достоинств и недостатков. Следует обратить внимание на типовые регуляторы, реализуемые на таких корректирующих устройствах: пропорциональные (П), пропорционально-интегральные (ПИ), пропорционально-интегро-дифференциальный (ПИД). Второе условие связано с расчетом САУ. На практике задачу сводят к расчету корректирующих устройств. При этом полагают, что вся система может быть разбита на неизменяемую часть и корректирующее устройство. Первую из них можно считать известной по результатам силового расчета и выбора элементов. Поэтому задача синтеза САУ локализуется на уровне расчета лишь корректирующего устройства. Необходимо иметь представление о методах получения параметров корректирующих устройств, уметь пользоваться методом логарифмических частотных характеристик. Следует знать еще один метод синтеза – модальный. Его использование предполагает получение решения в два этапа. На первом выбирается желаемое расположение полюсов, т.е. такое, при котором выполняются требования по качеству САУ. На втором осуществляется собственно синтез регулятора. Он заключается в нахождении матрицы обратной связи по вектору состояния, которая обеспечивает расположение полюсов замкнутой системы желаемым образом. 2.7.2. Контрольные вопросы 1. Какой участок ЛАЧХ оказывает преимущественное влияние на качество переходного процесса системы? 2. Какой наклон должна иметь среднечастотная асимптота желаемой ЛАЧХ? 3. Запишите выражение для ПИД-закона управления. 4. Известны передаточные функции системы с единичной отрицательной обратной связью: Желаемая ПФ разомкнутой системы и ПФ неизменяемой части:
Найти передаточную функцию корректирующего устройства алгебраическим способом. 5. Решить предыдущую задачу, если вместо передаточной функции
6. Получить уравнение замкнутой системы, если в разомкнутом состоянии она описывается уравнениями 7. Каким условиям должна удовлетворять матрица Восьмой семестр 2.8. Нелинейные системы автоматического управления Типовые нелинейности в элементах и системах управления. Математические модели и структурные схемы нелинейных систем и методы их преобразования. Особенности режимов функционирования нелинейных САУ. Методы анализа процессов в нелинейных САУ. Метод фазового пространства и метод припасовывания. Метод гармонической линеаризации. Критерии устойчивости нелинейных динамических систем. Второй метод А. М. Ляпунова. Метод абсолютной устойчивости В. М. Попова. Методические указания Изучение нелинейных систем начинают с четкого уяснения понятий «нелинейная зависимость», «нелинейное звено». Для облегчения этого этапа все нелинейности разделяют на статические и динамические. Первые полно и точно описываются нелинейными статическими характеристиками, вторые – нелинейными дифференциальными уравнениями. Дальнейшие меры, облегчающие изучение нелинейных САУ, связаны с введением типовых нелинейностей. Они позволяют унифицировать математические описания почти всего многообразия реальных нелинейных элементов. В результате, многие нелинейные системы могут быть представлены в виде последовательно соединенных нелинейной и линейной частей САУ. Это типовая форма и для ее исследования можно применить типовые методики, что значительно упрощает задачу анализа. Для расчета представленных таким образом систем управления используют какой-либо метод из имеющейся сравнительно большой совокупности. Отметим, что наличие многих методов порождено трудностями решения нелинейных задач. Все методы разделяют на две основные группы: точные и приближенные. Из числа точных методов следует знать метод фазовой плоскости, второй (прямой) метод А.М. Ляпунова, метод исследования абсолютной устойчивости В.М Попова. Из группы приближенных нужно знать метод гармонической линеаризации и уметь применять его для определения автоколебаний и устойчивости нелинейных систем. 2.8.2. Контрольные вопросы 1. Распространяется ли на нелинейные системы принцип, в соответствии с которым реакция системы на два внешних воздействия равна сумме реакций системы, полученных для каждого из воздействий порознь? 2. Какую типовую нелинейность можно использовать для описания зависимости силы сухого трения
3. Система описывается уравнением 4. Сколько листов используется при построении фазового портрета системы с нелинейностью, представленной в вопросе 2. 5. Необходимое или достаточное условие проверяется по критерию В.М. Попова? Методические указания Класс дискретных систем в настоящее время становится все более значимым в связи с все более широким применением цифровых устройств для реализации регуляторов, датчиков обратной связи и других элементов САУ. Для изучения дискретных САУ необходимо обратиться к материалам курса «Математические основы кибернетики» и восстановить в памяти сведения по квантованию сигналов по времени и уровню, видам модуляции, разностным уравнениям, применению z -преобразования для описания процессов в импульсных системах. Следует разобраться в терминологии, различая принципиальные особенности импульсных и цифровых систем управления. Для лучшего понимания физического смысла импульсных систем целесообразно подробно рассмотреть их частотные характеристики. Обратите внимание на получение по ним основного результата теоремы Котельникова - Шенона – определение частоты квантования, обеспечивающей неискаженную передачу сигнала дискретным способом. Необходимо знать и уметь находить частоту квантования по частотным и временным характеристикам неизменяемой части системы. Необходимым условием работоспособности дискретной САУ является ее устойчивость. Необходимо уметь анализировать это свойство САУ по корням характеристического уравнения. Нужно знать способ использования билинейного преобразования для привлечения к анализу устойчивости дискретных САУ критериев, разработанных для непрерывных систем. Следует уметь применять билинейное преобразование для синтеза цифровых регуляторов методом ЛАЧХ. 2.9.2 Контрольные вопросы 1. Какой вид квантования реализуется в цифровых системах? 2. Является ли линейной система с широтно-импульсной модуляцией? 3. При каком соотношении между полосой 4. Запишите выражение выходного сигнала 5. Определите передаточную функцию импульсной системы по ее разностному уравнению
6. В каких случаях справедливо равенство
7. Устойчива ли система, имеющая полюсы 8. Определить цену младшего разряда 4-х разрядного аналого-цифрового преобразователя, имеющего максимальный входной сигнал Методические указания Важным этапом в изучении адаптивных систем является ознакомление с их классификацией. Для уяснения особенностей рассматриваемого класса систем желательно привести примеры объектов, управление которыми целесообразно осуществлять с использованием адаптации. Полезно нарисовать схемы систем экстремального управления, использующие запоминание экстремума, синусоидальный поисковый сигнал, способ синхронного детектирования. 2.10.2. Контрольные вопросы 1. Приведите два-три примера объектов, для которых недостаток знаний об объектах делает необходимым использование принципов адаптации. 2. Приведите примеры объектов управления, имеющих экстремальные характеристики. 3. Какие способы определения градиента Вы знаете? 4. Какой из способов определения градиента связан с добавлением малых гармонических составляющих к основным (регулируемым) величинам? 5. Какие способы организации движения к экстремуму Вы знаете? 6. Почему движение к экстремуму по методу Гаусса–Зейделя не является кратчайшим? 7. Изобразите на плоскости (в случае двух регулируемых величин) процессы при поиске экстремума по методу Гаусса–Зейделя, градиента и наискорейшего спуска. СОДЕРЖАНИЕ ПРАКТИЧЕСКОГО РАЗДЕЛА ДИСЦИПЛИНЫ Восьмой семестр 5. Методы исследования нелинейных систем. Метод фазовой плоскости. Метод гармонической линеаризации. (2 часа). Перечень лабораторных работ Седьмой семестр 1. Моделирование линейных систем на АВК - 6 (2 часа). 2. Исследование частотных характеристик линейных систем управления (2 часа). 3. Стабилизация структурно-неустойчивых САУ (3 часа). 4. Исследование принципов построения регуляторов линейных САР (3 часа). Восьмой семестр 5. Исследование переходных процессов в следящей системе с нелинейными звеньями (3 часа). 6. Исследование нелинейных систем методом фазовой плоскости (3 часа). КУРСОВЫЕ РАБОТЫ Общие методические указания Учебным планом предусмотрено выполнение двух курсовых работ в седьмом и восьмом семестрах. Суть курсовых работ состоит в практическом применении знаний, полученных в курсе “Теория автоматического управления”, а также курсах “Математические основы кибернетики”, “Прикладное программирование” и некоторых других, для решения задач построения и исследования системы автоматического управления динамическим объектом. Объем каждой курсовой работы планируется из расчета затрат на нее студентами 50 часов. Ориентировочный объем расчетно-пояснительной записки - 20-30 страниц формата А4. Законченная курсовая работа оформляется в виде пояснительной записки. Пояснительная записка должна соответствовать стандарту ТПУ 2.5.01-2006 «Работы выпускные квалификационные, проекты и работы курсовые. Структура и правила оформления». Пояснительная записка должна включать в указанной ниже последовательности: титульный лист, задание, содержание, введение, основную часть, заключение, список использованных источников, приложения. Основная часть пояснительной записки должна подробно отражать ход и результаты исследования по всем пунктам программы. В ней, однако, не должно быть переписанных текстов из учебников, учебных пособий, монографий или других изданий. Терминология, обозначения и определения должны быть едиными по всей записке и соответствовать общепринятым в научно-технической литературе. Сокращения слов в тексте и подписях под иллюстрациями не допускаются. Все обозначения электрических, механических и других физических величин должны быть приведены в системе СИ.
Курсовая работа №1 Работа состоит из двух частей. Первая часть включает разработку структуры и описание функционирования системы автоматического управления некоторым техническим объектом. Для выполнения этой части работы необходимо познакомиться с описаниями различных систем автоматического управления, которые, как правило, содержатся в большинстве учебников по ТАУ [1, 2, 5, 6, 8, 10] Вторая часть работы включает получение и исследование линейной математической модели замкнутой системы. К основным разделам первой части курсовой работы относятся: - разработка функциональной схемы системы автоматического регулирования заданного технического объекта, включающей устройство сравнения, исполнительный, усилительно-преобразовательный и информационно-измерительный блоки; - описание принципа работы САР с анализом области применения и границ работоспособности предложенной схемы; - выбор элементного состава исполнительного и информационно-измерительного блоков предложенной системы. Вторая часть работы включает: - получение модели динамического объекта в форме операторно-структурной схемы и передаточной функции; - построение и анализ частотных характеристик модели; - анализ точностных и динамических характеристик замкнутой системы при детерминированных входных воздействиях. Исходные данные к выполнению первой курсовой работы изложены в Методических указаниях по выполнению курсовой работы №1 по ТАУ. 4.2.1 Выбор варианта курсовой работы 1 Вариант индивидуального задания для первой части курсовой работы включает тип системы управления динамическим объектом. Для второй части – схему системы автоматического регулирования и ее параметры. Вариант определяется как число, со
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 374; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.27.70 (0.017 с.) |


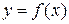 , где
, где  - входной сигнал на систему, а
- входной сигнал на систему, а 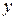 - ее выходной сигнал. Таким образом, систему можно рассматривать как некоторый оператор
- ее выходной сигнал. Таким образом, систему можно рассматривать как некоторый оператор 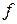 , преобразующий входной сигнал в выходной. Оператор называется линейным, если справедливы два соотношения
, преобразующий входной сигнал в выходной. Оператор называется линейным, если справедливы два соотношения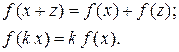
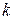 раз, реакция также меняется в
раз, реакция также меняется в  ,
,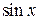 нелинеен, так как
нелинеен, так как 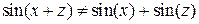 . Линейная модель включает только линейные операторы, а нелинейная, содержит хотя бы один нелинейный оператор.
. Линейная модель включает только линейные операторы, а нелинейная, содержит хотя бы один нелинейный оператор. , где x и y – соответственно входной и выходной сигналы?
, где x и y – соответственно входной и выходной сигналы?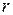 ?
?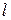 выходов, определите размерность передаточной матричной функции.
выходов, определите размерность передаточной матричной функции.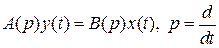 определяет ее устойчивость?
определяет ее устойчивость?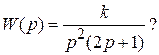
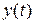 .
.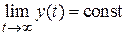 , то установившийся режим называется статическим. Он является характерным для устойчивых систем, на вход которых подан сигнал
, то установившийся режим называется статическим. Он является характерным для устойчивых систем, на вход которых подан сигнал  , удовлетворяющий условию
, удовлетворяющий условию  .
.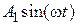 и сигналы, описываемые полиномиальными выражениями вида
и сигналы, описываемые полиномиальными выражениями вида 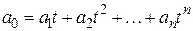 . При подаче их на вход системы на ее выходе можно выделить свободную составляющую, которая со временем затухает, и вынужденную. Последняя не отвечает условию
. При подаче их на вход системы на ее выходе можно выделить свободную составляющую, которая со временем затухает, и вынужденную. Последняя не отвечает условию 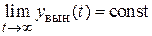 , но, тем не менее, является характеристикой существующего в системе установившегося динамического режима. Так в случае гармонического входного сигнала
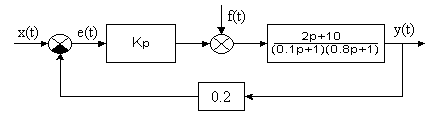
, но, тем не менее, является характеристикой существующего в системе установившегося динамического режима. Так в случае гармонического входного сигнала 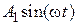 выходной сигнал по истечении времени, достаточного для затухания свободной составляющей, будет иметь вид
выходной сигнал по истечении времени, достаточного для затухания свободной составляющей, будет иметь вид 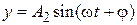 ,
, 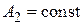 ,
, 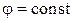 .
.
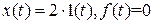 , б)
, б) 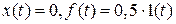 ?
?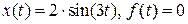 ?
?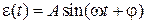 в установившемся режиме системы (см. вопрос 1), если
в установившемся режиме системы (см. вопрос 1), если  ,
, 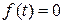 ?
?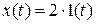 ,
, 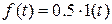 ?
?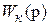 обеспечивающей инвариантность координаты
обеспечивающей инвариантность координаты 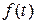 .
.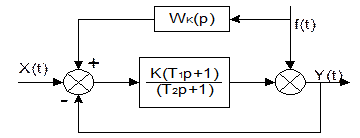
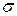 и длительность переходного процесса по характеристике
и длительность переходного процесса по характеристике 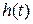 , представленной на рис. 2.3.
, представленной на рис. 2.3.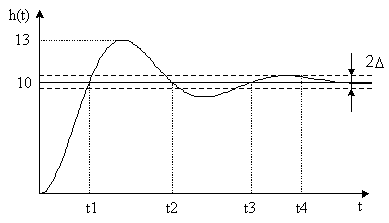
 используется для оценивания длительности переходного процесса?
используется для оценивания длительности переходного процесса?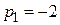 является ближайшим к мнимой оси?
является ближайшим к мнимой оси?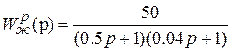 ,
,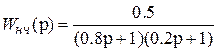 .
.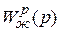 известна желаемая передаточная функция замкнутой системы
известна желаемая передаточная функция замкнутой системы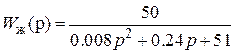 .
.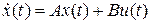 ,
, 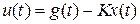 ,
, 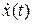 - вектор состояния и его производная,
- вектор состояния и его производная, 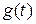 ,
, 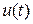 - векторы входного сигнала и управления,
- векторы входного сигнала и управления, 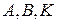 – матрицы.
– матрицы.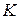 в предыдущей задаче при создании модального регулятора?
в предыдущей задаче при создании модального регулятора? от скорости движения
от скорости движения 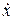 :
:
 ?
?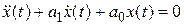 . Найти уравнение фазовых траекторий
. Найти уравнение фазовых траекторий 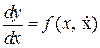 .
.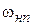 пропускания непрерывной части системы и частотой квантования
пропускания непрерывной части системы и частотой квантования 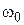 обеспечивается эквивалентность динамических свойств непрерывной системы и ее дискретного аналога?
обеспечивается эквивалентность динамических свойств непрерывной системы и ее дискретного аналога?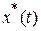 идеального импульсного элемента при подаче входного сигнала
идеального импульсного элемента при подаче входного сигнала 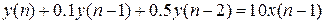 .
.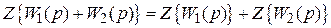 ?
?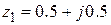 ,
,  ?
?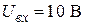 .
.


