Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Фундаментальные свойства управляемых объектов и системСодержание книги
Поиск на нашем сайте
Управляемость и наблюдаемость. Устойчивость динамических систем в малом, в большом и в целом. Асимптотическая устойчивость. Методы оценки устойчивости систем по А. М. Ляпунову. Устойчивость линейных стационарных непрерывных систем. Частотные критерии устойчивости линейных стационарных непрерывных систем. Запасы устойчивости. Критические коэффициенты передачи систем. Методические указания Следует знать основные понятия, определяющие фундаментальные свойства объектов и систем управления. В практическом плане важнейшим свойством является устойчивость САУ. Поэтому следует знать понятие устойчивости, физическое содержание этого свойства, методы и меры его оценивания. Обратите внимание на практические способы оценивания устойчивости систем – по расположению полюсов замкнутой системы и по частотным характеристикам. Важно знать и уметь оценивать запасы устойчивости, что позволяет сравнивать различные варианты расчетов САУ при проектировании. 2.4.2. Контрольные вопросы 1. О какой устойчивости состояний или процессов в нелинейной САУ можно судить по корням характеристического уравнения ее линеаризованной модели (в малом, в большом, в целом)? 2. Какое математическое выражение из состава дифференциального уравнения системы 3. Вынужденная или свободная составляющая решения дифференциального уравнения системы используется для анализа ее устойчивости? 4. Что можно сказать об устойчивости системы, если характеристический полином ее линеаризованной модели содержит нулевой корень? 5. Устойчива ли САУ второго порядка, если все коэффициенты ее характеристического уравнения положительны? 6. Будет уменьшаться или увеличиваться запас устойчивости САУ при увеличении коэффициента передачи устойчивой в разомкнутом состоянии системы? 7. Определите значения коэффициента передачи
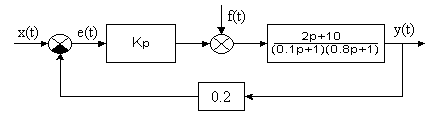
Установившиеся процессы в линейных системах управления Статические режимы в линейных системах управления. Статическое и астатическое управление. Способы определения астатизма в линейных системах. Установившиеся динамические режимы в линейных элементах и системах управления и способы их анализа. Методы повышения точности линейных САУ в установившихся режимах. Методические указания В этом разделе изучаются установившиеся режимы в системах управления. Режимы подразделяют на два вида в зависимости от свойств выходного сигнала Если Режим второго вида устанавливается в устойчивой системе при подаче на ее вход сигнала, не отвечающего условию Выделенные два режима имеют важное прикладное значение. При рассмотрении первого режима оценивают величину статической ошибки, которая и является мерой точности в статике. Однако чаще приходится решать обратную задачу: по заданной величине статической ошибки находят значения коэффициента передачи регулятора, при которых ошибка не будет превышать заданного значения. Нужно знать содержание этих задач и уметь их решать, в том числе получая решения, обеспечивающие нулевую статическую погрешность в так называемых астатических системах. Динамические установившиеся режимы также рассматриваются в прямых и обратных задачах. Прямые задачи позволяют, например, оценить ошибки по скорости движения, по ускорению, используя полиноминальные воздействия. Применение гармонических воздействий дает возможность найти максимальную величину ошибки в виде амплитуды установившихся колебаний. Обратные задачи решаются на этапе проектирования САУ, позволяя найти значение коэффициента передачи регулятора, при котором та или иная ошибка не превосходит заданного значения. Следует уметь решать прямую и обратную задачи в случае установившегося динамического режима. 2.5.2. Контрольные вопросы 1. Уменьшится ли величина статической ошибки при увеличении коэффициента передачи регулятора? Поясните ответ решением задачи на примере приведенной системы.
Рис. 2.1 2. Какое условие при размещении интегрирующего звена в прямом канале нужно выполнить, чтобы статическая ошибка за счет влияния возмущения была бы равна нулю? 3. Чему равно установившееся значение выходного сигнала y(t) системы (см. вопрос 1), если а) 4. Чему равен выходной сигнал 5. Чему равна амплитуда ошибки 6. Определите величину статической ошибки в системе (см. вопрос 1), если 7. Запишите выражение для передаточной функции
Рис. 2.2
|
||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 163; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.191.60 (0.006 с.) |

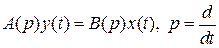 определяет ее устойчивость?
определяет ее устойчивость?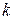 , при которых замкнутая система устойчива, если обратная связь отрицательная единичная и разомкнутая система имеет передаточную функцию
, при которых замкнутая система устойчива, если обратная связь отрицательная единичная и разомкнутая система имеет передаточную функцию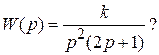
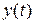 .
.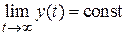 , то установившийся режим называется статическим. Он является характерным для устойчивых систем, на вход которых подан сигнал
, то установившийся режим называется статическим. Он является характерным для устойчивых систем, на вход которых подан сигнал  , удовлетворяющий условию
, удовлетворяющий условию  .
.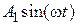 и сигналы, описываемые полиномиальными выражениями вида
и сигналы, описываемые полиномиальными выражениями вида 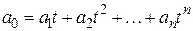 . При подаче их на вход системы на ее выходе можно выделить свободную составляющую, которая со временем затухает, и вынужденную. Последняя не отвечает условию
. При подаче их на вход системы на ее выходе можно выделить свободную составляющую, которая со временем затухает, и вынужденную. Последняя не отвечает условию 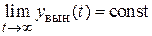 , но, тем не менее, является характеристикой существующего в системе установившегося динамического режима. Так в случае гармонического входного сигнала
, но, тем не менее, является характеристикой существующего в системе установившегося динамического режима. Так в случае гармонического входного сигнала 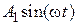 выходной сигнал по истечении времени, достаточного для затухания свободной составляющей, будет иметь вид
выходной сигнал по истечении времени, достаточного для затухания свободной составляющей, будет иметь вид 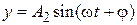 ,
, 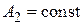 ,
, 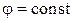 .
.
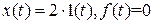 , б)
, б) 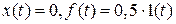 ?
?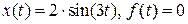 ?
?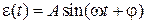 в установившемся режиме системы (см. вопрос 1), если
в установившемся режиме системы (см. вопрос 1), если  ,
, 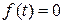 ?
?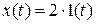 ,
, 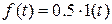 ?
?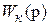 обеспечивающей инвариантность координаты
обеспечивающей инвариантность координаты 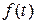 .
.