
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дискретные системы автоматического управленияСодержание книги
Поиск на нашем сайте
Классификация дискретных САУ по способам квантования сигналов. Математическое описание процессов в импульсных и цифровых системах. Использование дискретных операторных преобразований для описания процессов в дискретных САУ. Передаточные функции и частотные характеристики дискретных систем. Спектры дискретных сигналов. Теорема Котельникова-Шеннона и ее использование для анализа свойств дискретных систем. Анализ устойчивости состояний равновесия и процессов в дискретных системах. Методы анализа установившихся и переходных процессов в дискретных САУ. Методические указания Класс дискретных систем в настоящее время становится все более значимым в связи с все более широким применением цифровых устройств для реализации регуляторов, датчиков обратной связи и других элементов САУ. Для изучения дискретных САУ необходимо обратиться к материалам курса «Математические основы кибернетики» и восстановить в памяти сведения по квантованию сигналов по времени и уровню, видам модуляции, разностным уравнениям, применению z -преобразования для описания процессов в импульсных системах. Следует разобраться в терминологии, различая принципиальные особенности импульсных и цифровых систем управления. Для лучшего понимания физического смысла импульсных систем целесообразно подробно рассмотреть их частотные характеристики. Обратите внимание на получение по ним основного результата теоремы Котельникова - Шенона – определение частоты квантования, обеспечивающей неискаженную передачу сигнала дискретным способом. Необходимо знать и уметь находить частоту квантования по частотным и временным характеристикам неизменяемой части системы. Необходимым условием работоспособности дискретной САУ является ее устойчивость. Необходимо уметь анализировать это свойство САУ по корням характеристического уравнения. Нужно знать способ использования билинейного преобразования для привлечения к анализу устойчивости дискретных САУ критериев, разработанных для непрерывных систем. Следует уметь применять билинейное преобразование для синтеза цифровых регуляторов методом ЛАЧХ. 2.9.2 Контрольные вопросы 1. Какой вид квантования реализуется в цифровых системах? 2. Является ли линейной система с широтно-импульсной модуляцией? 3. При каком соотношении между полосой 4. Запишите выражение выходного сигнала 5. Определите передаточную функцию импульсной системы по ее разностному уравнению
6. В каких случаях справедливо равенство
7. Устойчива ли система, имеющая полюсы 8. Определить цену младшего разряда 4-х разрядного аналого-цифрового преобразователя, имеющего максимальный входной сигнал Адаптивные и экстремальные системы Основные задачи и способы адаптации систем управления. Классификация адаптивных систем. Постановка задач экстремального управления. Методы и средства автоматического поиска экстремума функции многих переменных. Экстремальные системы с определением производных по времени, с синхронным детектированием и запоминанием экстремума. Способы организации движений к экстремуму. Метод Гаусса-Зейделя, метод градиента, метод наискорейшего спуска. Методические указания Важным этапом в изучении адаптивных систем является ознакомление с их классификацией. Для уяснения особенностей рассматриваемого класса систем желательно привести примеры объектов, управление которыми целесообразно осуществлять с использованием адаптации. Полезно нарисовать схемы систем экстремального управления, использующие запоминание экстремума, синусоидальный поисковый сигнал, способ синхронного детектирования. 2.10.2. Контрольные вопросы 1. Приведите два-три примера объектов, для которых недостаток знаний об объектах делает необходимым использование принципов адаптации. 2. Приведите примеры объектов управления, имеющих экстремальные характеристики. 3. Какие способы определения градиента Вы знаете? 4. Какой из способов определения градиента связан с добавлением малых гармонических составляющих к основным (регулируемым) величинам? 5. Какие способы организации движения к экстремуму Вы знаете? 6. Почему движение к экстремуму по методу Гаусса–Зейделя не является кратчайшим? 7. Изобразите на плоскости (в случае двух регулируемых величин) процессы при поиске экстремума по методу Гаусса–Зейделя, градиента и наискорейшего спуска. СОДЕРЖАНИЕ ПРАКТИЧЕСКОГО РАЗДЕЛА ДИСЦИПЛИНЫ
|
||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 330; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.219.11 (0.009 с.) |

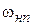 пропускания непрерывной части системы и частотой квантования
пропускания непрерывной части системы и частотой квантования 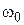 обеспечивается эквивалентность динамических свойств непрерывной системы и ее дискретного аналога?
обеспечивается эквивалентность динамических свойств непрерывной системы и ее дискретного аналога?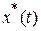 идеального импульсного элемента при подаче входного сигнала
идеального импульсного элемента при подаче входного сигнала  .
.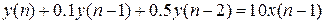 .
.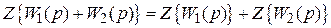 ?
?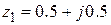 ,
,  ?
?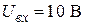 .
.


