
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Передача теплоты через плоскую однослойную и многослойную стенки и граничных условиях III родаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Необходимо найти тепловой поток от горячей жидкости к холодной и температуры на поверхности стенки. Плотность теплового потока от горячей жидкости к стенке определяется по уравнению Ньютона-Рихмана: q = a1 (tж1 – tс1). При стационарном тепловом режиме та же плотность теплового потока, обусловленная теплопроводностью через твердую стенку будет равна:
Тот же тепловой поток передается от второй поверхности стенки к холодной жидкости за счет теплоотдачи: q = a2 (tс2 – tж2). Представленные выражения можно записать в виде:
Складывая почленно полученные равенства, получим:
Отсюда плотность теплового потока равна:
Обозначим Тогда где k – коэффициент теплопередачи, Вт/(м2×К). Коэффициент теплопередачи k характеризует интенсивность передачи теплоты от одной жидкости к другой через разделяющую их стенку и численно равен количеству теплоты, которое передается через единицу поверхности стенки в единицу времени при разности температур между жидкостями в один градус. Величина, обратная коэффициенту теплопередачи, называется полным термическим сопротивлением теплопередачи, (м2×К)/Вт:
где
Для многослойной стенки нужно учитывать термическое сопротивление каждого слоя. Если стенка состоит из n слоев, то полное термическое сопротивление теплопередачи через такую стенку будет равно:
отсюда Плотность теплового потока через многослойную стенку, состоящую из n слоев, будет равна:
Тепловой поток Q через поверхность F твердой стенки равен:
Температуры поверхностей однородной стенки можно найти из уравнений:
Температура на границе любых двух слоев i и i + 1 при граничных условиях третьего рода может быть определена по уравнению:
Лекция Тема: «ТЕПЛОПРОВОДНОСТЬ ПРИ СТАЦИОНАРНОМ РЕЖИМЕ» (продолжение) План. 4. Передача теплоты через цилиндрическую стенку и граничных условиях I рода. 5. Передача теплоты через многослойную цилиндрическую стенку и граничных условиях I рода. 6. Передача теплоты через однослойную и многослойную цилиндрические стенки и граничных условиях III рода 7. Критический диаметр цилиндрической стенки. 8. Передача теплоты через ребристую стенку. 9. Теплопроводность при наличии внутренних источников теплоты.
Передача теплоты из одной подвижной среды (жидкости или газа) к другой через разделяющую их однородную или многослойную твердую стенку любой формы называется теплопередачей. Теплопередача включается в себя теплоотдачу от более горячей жидкости к стенке, теплопроводность в стенке, теплоотдачу от стенки к более холодной среде. Передача теплоты через цилиндрическую стенку И граничных условиях I рода
постоянные температуры tc1 и tc2. В заданном интервале температур l =const. Необходимо найти распределение температур в цилиндрической стенке и тепловой поток через нее. В рассматриваемом случае дифференциальное уравнение теплопроводности удобно записать в цилиндрической системе координат:
При этом ось Oz совмещена с осью трубы. При заданных условиях температура изменяется только в радиальном направлении и температурное поле будет одномерным, поэтому:
Кроме того, так как температуры на наружной и внутренней поверхностях трубы неизменны, изотермические поверхности являются цилиндрическими. Тогда температура не должна изменяться вдоль j, то есть:
Следовательно, дифференциальное уравнение теплопроводности примет вид:
Граничные условия задаются следующим образом: t = tc1 при r = r1; t = tc2 при r = r2. Для решения дифференциального уравнения введем новую переменную:
Тогда дифференциальное уравнение примет вид:
Интегрируя, получаем:
Потенцируя и переходя к первоначальным переменным, получаем:
После интегрирования находим:
Подставим в полученное выражение граничные условия:
Тогда температурное поле будет равно:
Полученное выражение представляет собой уравнение логарифмической кривой. Криволинейное распределение температуры в цилиндрической стенке объясняется следующим. Для плоской стенки плотность теплового потока q остается одинаковой для всех изотермических поверхностей. Для цилиндрической стенки q через любую изотермическую поверхность зависит от радиуса. Для нахождения количества теплоты, проходящего через цилиндрическую поверхность площадью F в единицу времени, воспользуемся законом Фурье:
Очевидно, Тогда Q равно:
Из полученного выражения видно, что так же, как и для плоской стенки, тепловой поток через цилиндрическую оболочку прямо пропорционален разности температур поверхностей стенки. Тепловой поток может быть отнесен либо к единице длины трубы, либо к единице внутренней или внешней поверхности. При этом расчетные формулы для плотности теплового потока, принимают вид:
ql также называется линейной плотностью теплового потока (Вт/м). Как видно из первых двух уравнений плотности теплового потока q1 и q2 (отнесенные к внутренней и внешней поверхности) при передаче теплоты через трубы неодинаковы, причем всегда q1 > q2. Связь между величинами q1, q2 и ql следующая:
|
||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 439; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.88.104 (0.007 с.) |


 .
. ,
, ,
, .
. .
. .
. .
. ,
,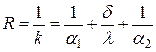 ,
, и
и  - термическое сопротивление стенки.
- термическое сопротивление стенки.
 ,
, .
. .
. .
. ;
;  или
или  .
. .
.
 .
. и
и  .
. и
и 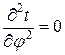 .
. .
.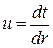 Þ
Þ  .
. .
. Þ
Þ  .
. Þ
Þ  .
.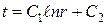 .
. ,
,


 ;
;  .
. ,
, или
или  .
. .
. ;
;  .
. .
. - тепловой поток через единицу внутренней поверхности;
- тепловой поток через единицу внутренней поверхности;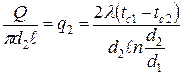 - тепловой поток через единицу наружной поверхности;
- тепловой поток через единицу наружной поверхности; - поток теплоты, проходящий через единицу длины трубы.
- поток теплоты, проходящий через единицу длины трубы. .
.


