
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теплопередача. Основные формулы передачи теплоты и законы.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Теплопередача. Основные формулы передачи теплоты и законы. Теплопередача (теория теплообмена) - называется наука изучающая процессы передачи теплоты между телами, распространение теплоты в пространстве и распределение температуры в твердых, жидких и газообразных телах. Три основные формы передачи теплоты: теплопроводность, конвективный теплообмен и лучистый теплообмен. Теплопроводность представляет собой форму распространения теплоты путем непосредственного соприкосновения отдельных частиц тела, имеющих различную температуру. При этом процесс теплообмена происходит за счет передачи энергии микродвижения одних частиц другим Конвективным теплообменном называется форма переноса теплоты, в пространстве, осуществляемая перемещающимися частицами жидкости (капельная жидкость или газ). При перемещении в пространстве различно нагретых частиц жидкости происходит непосредственное их соприкосновение, поэтому здесь имеет место теплопроводность. Следовательно конвективный теплообмен представляет собой совокупное действие двух процессов – конвекции и теплопроводности. В зависимости от причины вызывающей движение жидкости, различают конвективный теплообмен при свободном движении жидкости (свободная конвекция) и конвективный теплообмен при вынужденном движении жидкости (вынужденная конвекция). Тепловым излучением называется процесс переноса теплоты в пространстве электромагнитными волнами. Лучистым теплообменом, или тепловым излучением называется форма передачи теплоты излучением между телами, который включает последовательное превращение внутренней энергии тела в энергию излучения, распространение ее в пространстве и превращение энергии излучения во внутреннюю энергию другого тела. Температурное поле Совокупность значений температуры
Температурный градиент Если соединить точки тела, имеющие одинаковую температуру, получим поверхность равных температур, называемую изотермической. Изотермической поверхностью тела называется геометрическое место точек, имеющих одинаковую температуру. Температурный градиент есть вектор направленный по нормали к изотермической поверхности в сторону возрастания температуры и численно равный пределу отношения изменения температуры
Тепловой поток Количества теплоты Q, проходящее в единицу времени через изотермическую поверхность F, называется тепловым потоком. Тепловой поток, приходящийся на единицу поверхности, называется удельным тепловым потоком, плотностью теплового потока или тепловой нагрузкой поверхности q. Если градиент температуры для различных точек поверхности различный, то количество теплоты через всю изотермическую поверхность в единицу времени равно
Теплопроводность. Закон Фурье. Коэффициент теплопроводности. Необходимым условием распространения теплоты являетсянеравномерность распределения температуры в рассматриваемой среде. Таким образом, для передачи теплоты теплопроводностью необходимо неравенство нулю температурного градиента в различных точках тела. Закон Фурье:
Согласно закону Фурье количество теплоты проходящий через элемент изотермической поверхности
где Количество теплоты, проходящее в единицу времени через единицу площади изотермической поверхности Дифференциальные уравнения конвективного теплообмена. Основные понятия. Дифференциальное уравнение теплообмена получается при рассмотрении передачи теплоты теплопроводностью через, практический, неподвижный слой жидкости (пограничный слой), который имеет место вблизи твердого тела, омываемого жидкостью (
Дифференциальное уравнение энергии при условии однородности и несжимаемости жидкости, отсутствия внутренних источников теплоты и работы расширения, а также постоянства физических параметров жидкости в пределах элементарного объема формулируется следующим образом:
Дифференциальное уравнение неразрывности получается на основе закона сохранения массы и, для сжимаемой жидкости имеет следующий вид:
Уравнение движения (уравнение Навье-Стокса) получается на базе первого и второго законов Ньютона и в векторной форме записи можно представить в виде
Понятия о теории подобия. Для подобия физических процессов необходимо говорить о подобии физических величин и явлений. Два или несколько явлений будут подобны, если подобны все физические величины, характеризующие эти явления, т.е. подобные между собою явления имеют одинаковые безразмерные комплексы - критерии подобия. Этот вывод свидетельствует о том, что в опытах нужно измерять те величины, которые входят в критерии подобия, характеризующие данный процесс. Важной теоремой теории подобия является утверждение о том, что решение дифференциального уравнения, описывающего данный процесс, может быть представлено в виде функциональной зависимости между критериями подобия, характеризующими этот процесс и полученными из исходного уравнения. Это утверждение говорит о том, опытные данные надо обработать в виде зависимости между критериями подобия. Наряду с приведенными выше двумя теоремами подобия, важным является и утверждение о том, что подобны между собой те явления, которые принадлежат к одному классу, к одному роду и имеют равные определяющие критерии подобия. Этот вывод позволяет полученные в опыте расчетные зависимости распространить на группу явлений, подобных исследованному. Таким образом, теория подобия, при наличии дифференциальных уравнений, описывающих рассматриваемый процесс, позволяет, не решая сами уравнения, получить выражения чисел (критериев) подобия и на их основе получить расчетные зависимости – уравнения подобия. Теплообмен при кипении. Опыт показывает, что температура кипящей жидкости всегда несколько выше температуры кипения ts. Она остается почти постоянной в направлении от свободного уровня к поверхности теплообмена (рис. 14) и лишь в слое толщиной 2 – 5 мм у самой стенки резко возрастает. Следовательно, в прилегающем к стенке слое жидкость перегрета на Δt=t – ts; эта величина называется температурным напором.
В начале кипения -область А (Рис. 15) при Δt = 0 - 5 ºС, q= 100 – 5600 Вт/м2 значение коэффициента теплоотдачи невелико и определяется условиями свободной конвекции однофазной жидкости. При дальнейшем кипении и повышении Δt значения коэффициентов теплоотдачи и q резко увеличиваются и при Δt = 25 ºС достигают своего максимального значения: αкр = 5,85·104 Вт/(м2·К), qкр = 1,45·106Вт/м2. Эту область, обозначенной на рис. 15 буквой В, называют областью пузырькового кипения. Последующее повышение Δt приводит к еще более интенсивному процессу образования пузырьков на твердой поверхности. Сливаясь затем между собой, они образуют общую паровую пленку. Образование паровой пленки приводит к резкому снижению интенсивности теплообмена между поверхностью и жидкостью, вследствие большого термического сопротивления пленки. Эта область, обозначена на рис. 15 буквой С и называется переходной областью. Следует отметить, что паровая пленка в этой области неустойчива. При дальнейшем увеличении перепада температур образовавшаяся на поверхности пленка становится устойчивой, интенсивность теплообмена продолжает падать. При некотором значении перепада температур процесс теплообмена стабилизируется, а коэффициент теплоотдачи имея при том минимальное значение, не зависит от перепада температур. Эта область обозначена на рис. 15 буквой D и называется областью пленочного кипения. В практических расчетах пузырькового кипения воды удобно пользоваться следующими уравнениями:
Зависимости (141) и (142)действительны в диапазоне давлений от 0,1 до 5 МПа. При пузырьковом кипении фреона 12 в диапазоне температур от – 40 до 10 ºС для определения α рекомендуется формула
При кипении фреона 11 может быть использована зависимость
В этих уравнениях q – в Вт/м2, р – в МПа, коэффициент теплоотдачи – Вт/(м2·К). При вынужденном турбулентном движении кипящей жидкости в трубах теплоотдача осуществляется по-разному. Если обозначить коэффициент теплоотдачи, полученный по формуле (141), αq, а коэффициент теплоотдачи, рассчитанный по уравнению подобия для однофазной жидкости (130), αw, то, как показывают опыты, при αq /αw <0,5 коэффициент теплоотдачи при пузырьковом кипении движущейся воды в трубе α=αw а при αq/αw>2; α=αq. В области 0,5 ≤ αq/αw ≤2 коэффициент теплоотдачи определяют по формуле
При пленочном кипении средний коэффициент теплоотдачи определяется следующим образом: на вертикальной поверхности
где λ п – коэффициент теплопроводности пара при температуре насыщения; μ п – динамический коэффициент вязкости пара при температуре насыщения; h – высота стенки, на горизонтальном цилиндре
где d – наружный диаметр цилиндра; ρ – плотность жидкости при температуре насыщения. Теплопередача. Основные формулы передачи теплоты и законы. Теплопередача (теория теплообмена) - называется наука изучающая процессы передачи теплоты между телами, распространение теплоты в пространстве и распределение температуры в твердых, жидких и газообразных телах. Три основные формы передачи теплоты: теплопроводность, конвективный теплообмен и лучистый теплообмен. Теплопроводность представляет собой форму распространения теплоты путем непосредственного соприкосновения отдельных частиц тела, имеющих различную температуру. При этом процесс теплообмена происходит за счет передачи энергии микродвижения одних частиц другим Конвективным теплообменном называется форма переноса теплоты, в пространстве, осуществляемая перемещающимися частицами жидкости (капельная жидкость или газ). При перемещении в пространстве различно нагретых частиц жидкости происходит непосредственное их соприкосновение, поэтому здесь имеет место теплопроводность. Следовательно конвективный теплообмен представляет собой совокупное действие двух процессов – конвекции и теплопроводности. В зависимости от причины вызывающей движение жидкости, различают конвективный теплообмен при свободном движении жидкости (свободная конвекция) и конвективный теплообмен при вынужденном движении жидкости (вынужденная конвекция). Тепловым излучением называется процесс переноса теплоты в пространстве электромагнитными волнами. Лучистым теплообменом, или тепловым излучением называется форма передачи теплоты излучением между телами, который включает последовательное превращение внутренней энергии тела в энергию излучения, распространение ее в пространстве и превращение энергии излучения во внутреннюю энергию другого тела. Температурное поле Совокупность значений температуры
Температурный градиент Если соединить точки тела, имеющие одинаковую температуру, получим поверхность равных температур, называемую изотермической. Изотермической поверхностью тела называется геометрическое место точек, имеющих одинаковую температуру. Температурный градиент есть вектор направленный по нормали к изотермической поверхности в сторону возрастания температуры и численно равный пределу отношения изменения температуры
Тепловой поток Количества теплоты Q, проходящее в единицу времени через изотермическую поверхность F, называется тепловым потоком. Тепловой поток, приходящийся на единицу поверхности, называется удельным тепловым потоком, плотностью теплового потока или тепловой нагрузкой поверхности q. Если градиент температуры для различных точек поверхности различный, то количество теплоты через всю изотермическую поверхность в единицу времени равно
|
||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 2132; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.191.241 (0.009 с.) |

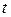 в данный момент времени
в данный момент времени  для всех точек пространства, определяемых координатами
для всех точек пространства, определяемых координатами  называется температурным полем
называется температурным полем
 к расстоянию между изотермами по нормали
к расстоянию между изотермами по нормали 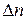 (К/м)
(К/м)
 , где Q – тепловой поток, Вm; dF – элемент изотермической поверхности, м.
, где Q – тепловой поток, Вm; dF – элемент изотермической поверхности, м.
 за промежуток времени
за промежуток времени  , пропорционально температурному градиенту
, пропорционально температурному градиенту ,
, – коэффициент пропорциональности есть физический параметр вещества и называется коэффициентом теплопроводности, Вт/(м·°C);
– коэффициент пропорциональности есть физический параметр вещества и называется коэффициентом теплопроводности, Вт/(м·°C);  , называется плотностью теплового потока.
, называется плотностью теплового потока.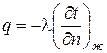 ) и передачи теплоты к пограничному слою за счет конвективного теплообмена (
) и передачи теплоты к пограничному слою за счет конвективного теплообмена ( ):
):






 (141)
(141) (142)
(142) (143)
(143) (144)
(144) (145)
(145) , (146)
, (146) , (147)
, (147)


